二叉树的前序、中序、后序遍历（非递归）

一、前中后序的非递归遍历

 代码中采用先序遍历的方法创建二叉树，示例创建二叉树格式如下：

创建过程中，以表示空节点。

代码：

#include <stdio.h>
#include <stdlib.h>

typedef struct BTNode{
    char data;
    struct BTNode *left;
    struct BTNode *right;
}BTNode,*BTree;

typedef struct Stack{
    BTree data[101];
    int top;
}BTStack;

typedef struct Post_BTNode{
    BTNode * Post_Node;
    int tag;
}Post_BTNode,*Post_BTree;

typedef struct Post_Stack{
    Post_BTNode data[101];
    int top;
}Post_Stack;

BTree CreatBTree(BTree root)//先序构建二叉树
{
   char data;
   scanf("%c",&data);
   getchar();
   if(data == '*')
        root = NULL;
   else{

        root = (BTree)malloc(sizeof(BTNode));
        root->data = data;
        root->left = CreatBTree(root->left);
        root->right = CreatBTree(root->right);
   }
   return root;
}

void PreOrder_NonRec(BTree root)//先序遍历非递归
{
    BTStack stack;
    stack.top = -1;
    BTNode *p=NULL;
    if(NULL != root)
    {
        stack.data[++stack.top] = root;
        while(stack.top > -1)
        {
            p = stack.data[stack.top--];
            printf(" %c",p->data);
            if(NULL != p->right)
                stack.data[++stack.top] = p->right;
            if(NULL != p->left)
                stack.data[++stack.top] = p->left;
        }
    }
    printf("\n");
}

void Inorder_NonRec(BTree root)//中序遍历非递归
{
    BTStack stack;
    BTNode *p = NULL;
    stack.top = -1;
    p = root;
    while(NULL != p || stack.top > -1)
    {
        while(NULL != p)
        {
            stack.data[++stack.top]=p;
            p = p->left;
        }
        p = stack.data[stack.top--];
        printf(" %c",p->data);
        p = p->right;
    }
    printf("\n");
}

void PostOrder_NonRec(BTree root)//后续遍历非递归
{
    Post_Stack stack;
    Post_BTNode node;
    BTNode * p=NULL;
    p= root;
    stack.top = -1;
    while(NULL != p || stack.top > -1)
    {
        while(NULL != p)
        {
            node.Post_Node=p;
            node.tag = 1;
            stack.data[++stack.top] = node;
            p = p->left;
        }
        node = stack.data[stack.top--];
        if(node.tag == 1)
        {
            node.tag = 2;
            stack.data[++stack.top] = node;
            p = node.Post_Node->right;
        }
        else if(node.tag == 2)
        {
            p = node.Post_Node;
            printf(" %c",p->data);
            p = NULL;
        }
    }
    printf("\n");
}

int main()
{
    BTree root=NULL;
    root = CreatBTree(root);
    printf("PreOrder:");
    PreOrder_NonRec(root);
    printf("InOrder:");
    Inorder_NonRec(root);
    printf("PostOrder:");
    PostOrder_NonRec(root);
    return 0;
}

运行结果：

二、根据前序和中序求后序

直接上代码（有注释）：

#include <stdio.h>
#include <string.h>
void preInToPost(char * pre,char * in, int size)
{
    if(size == 0)
    {
        return ;
    }
    char ch = *(pre+0);  //当前子树的根节点
    int rootIndex = 0;  //查找当前子树的根节点在中序遍历中的位置
    for(;rootIndex<size;rootIndex++)
    {
        if(ch == *(in+rootIndex))
        break;
    }
    preInToPost(pre+1,in,rootIndex); //递归根据左子树的前序和中序求后序
    preInToPost(pre+rootIndex+1,in+rootIndex+1,size-(rootIndex+1)); //递归根据右子树的前序中序求后序
    printf("%c",ch); //因为是后序序列，所以在左右子树输出完后输出当前根节点
}
int main()
{
    char * preOrder = "abchdefg"; //前序序列
    char * inOrder  = "hcbdafeg"; //中序序列
    int size = strlen(preOrder);
    printf("前序序列：%s\n",preOrder);
    printf("中序序列：%s\n",inOrder);
    printf("后序序列：");
    preInToPost(preOrder,inOrder,size);
    return 0;
}

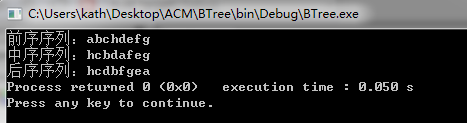
结果：