K近邻(KNN)
1 KNN 原理
K近邻学习是一种常用的监督学习方法,也是“懒惰学习”的代表(因为它没有显式的学习过程)。它的思想很简单:给定测试样本,基于某种距离度量找出训练集中与其最靠近的K个样本,然后基于对这K个“邻居”的投票进行预测。 KNN的建立过程很简单:
- 给定测试样本,计算它与训练集中每一个样本的距离;
- 找出距离最近的K个训练样本,作为测试样本的K个“邻居”;
- 依据这K个近邻归属的类别对测试样本进行投票预测。
例如,我们要决定绿色测试样本的类别归属,如果
K
=
3
K=3
K=3,它的3个近邻是实线圆内的3个训练样本,其中红色所占比例为
2
3
\frac{2}{3}
32,因此绿色被判别为红色的一类;如果
K
=
5
K=5
K=5,它的5个近邻为虚线圆内的训练样本,其中蓝色占比为
3
5
\frac{3}{5}
53,因此绿色被判别为蓝色的一类。
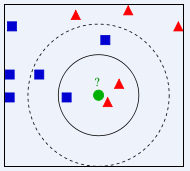
那么KNN中需要我们重点关注的两点就是:K值的选择和距离度量的计算。
1.1 模型优化
1.1.1 K值的选择
K值是该算法模型的一个超参数,一般情况下这个K和数据有很大的关系,都是用交叉验证进行选择的,但是建议 k ∈ [ 2 , 20 ] k\in[2,20] k∈[2,20]。k值还可以表示模型的复杂度,k值越小意味着模型复杂度越大,更容易过拟合,(用极少数的样例来决定这个预测的结果,很容易产生偏见)。k值越大学习的估计误差越小,但是学习的近似误差就会增大。
1.1.2 距离/相似度度量
我们一般使用
L
p
L_p
Lp距离进行度量,假设两个向量
(
x
i
,
x
j
)
(x_i,x_j)
(xi,xj)来自n维实向量空间
R
n
R^n
Rn,其中
x
i
=
(
x
i
(
1
)
,
x
i
(
2
)
,
…
,
x
i
(
n
)
)
,
x
j
=
(
x
j
(
1
)
,
x
j
(
2
)
,
…
,
x
j
(
n
)
)
x_i=(x_i^{(1)},x_i^{(2)},\dots,x_i^{(n)}), x_j=(x_j^{(1)},x_j^{(2)},\dots,x_j^{(n)})
xi=(xi(1),xi(2),…,xi(n)),xj=(xj(1),xj(2),…,xj(n)),则
x
i
,
x
j
x_i, x_j
xi,xj的
L
p
L_p
Lp距离定义为:
L
p
(
x
i
,
x
j
)
=
(
∑
l
=
1
n
∣
x
i
(
l
)
−
x
j
(
l
)
∣
p
)
1
p
L_{p}\left(x_{i}, x_{j}\right)=\left(\sum_{l=1}^{n}\left|x_{i}^{(l)}-x_{j}^{(l)}\right|^{p}\right)^{\frac{1}{p}}
Lp(xi,xj)=(l=1∑n∣∣∣xi(l)−xj(l)∣∣∣p)p1
- 当
p
=
1
p=1
p=1时,称为曼哈顿距离:
L 1 ( x i , x j ) = ∑ l = 1 n ∣ x i ( l ) − x j ( l ) ∣ L_{1}\left(x_{i}, x_{j}\right)=\sum_{l=1}^{n}\left|x_{i}^{(l)}-x_{j}^{(l)}\right| L1(xi,xj)=l=1∑n∣∣∣xi(l)−xj(l)∣∣∣ - 当
p
=
2
p=2
p=2时,称为欧氏距离:
L 2 ( x i , x j ) = ( ∑ l = 1 n ∣ x i ( l ) − x j ( l ) ∣ 2 ) 1 2 L_{2}\left(x_{i}, x_{j}\right)=\left(\sum_{l=1}^{n}\left|x_{i}^{(l)}-x_{j}^{(l)}\right|^{2}\right)^{\frac{1}{2}} L2(xi,xj)=(l=1∑n∣∣∣xi(l)−xj(l)∣∣∣2)21 - 当
p
=
∞
p=\infty
p=∞时,称为极大距离
L p ( x i , x j ) = max l n ∣ x i ( l ) − x j ( l ) ∣ L_{p}\left(x_{i}, x_{j}\right)=\max _{l} n\left|x_{i}^{(l)}-x_{j}^{(l)}\right| Lp(xi,xj)=lmaxn∣∣∣xi(l)−xj(l)∣∣∣
1.1.3 投票策略
- 投票决定,少数服从多数。取类别最多的为测试样本类别。
- 加权投票法,依据计算得出距离的远近,对近邻的投票进行加权,距离越近则权重越大,设定权重为距离平方的倒数。
1.2 KNN的应用
KNN虽然简单,但是既可以用来做分类,又可以用来做回归,还可以用来做缺失值填充。
- 在分类任务中常使用“投票法”。
- 在回归任务中可使用“平均法”,将这个K个近邻的实值输出标记的平均值作为预测结果。还可以使用加权平均。
1.3 泛化性能
假设测试样本维
x
x
x,其最近邻样本维
z
z
z,并且在
x
x
x的任意小范围
δ
\delta
δ总能找到一个训练样本
z
z
z,同时令
c
∗
=
a
r
g
m
a
x
c
∈
y
P
(
c
∣
x
)
c^*=arg\;max_{c∈y}P(c|x)
c∗=argmaxc∈yP(c∣x)为贝叶斯分类器的最优结果。那么最近了分类器出错的概率就是
x
x
x与
z
z
z的类别标记不同的概率:
P
(
e
r
r
)
=
1
−
∑
c
∈
y
P
(
c
∣
x
)
P
(
c
∣
z
)
≃
1
−
∑
c
∈
y
P
2
(
c
∣
x
)
≤
1
−
P
2
(
c
∗
∣
x
)
=
(
1
+
P
2
(
c
∗
∣
x
)
)
(
1
−
P
2
(
c
∗
∣
x
)
)
≤
2
×
(
1
−
P
2
(
c
∗
∣
x
)
)
P(err)=1-\sum_{c \in y}P(c|x)P(c|z)\\ \;\;\;\;\simeq 1-\sum_{c\in y}P^2(c|x)\\\leq1-P^2(c^*|x)\\ \qquad\qquad\qquad\quad=(1+P^2(c^*|x))(1-P^2(c^*|x))\\ \;\qquad\leq2\times\left(1-P^2(c^*|x)\right)
P(err)=1−c∈y∑P(c∣x)P(c∣z)≃1−c∈y∑P2(c∣x)≤1−P2(c∗∣x)=(1+P2(c∗∣x))(1−P2(c∗∣x))≤2×(1−P2(c∗∣x))
由此可见最近邻分类器虽然简单,但是其泛化错误率不超过贝叶斯最优分类器错误率的两倍。
2 代码实践
2.1 回归任务
导入所需库和数据集,此处使用sklearn数据集中的波士顿房价数据集,并使用head()函数查看数据集。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
plt.style.use("ggplot")
import seaborn as sns
from sklearn import datasets
boston = datasets.load_boston() # 返回一个类似于字典的类
X = boston.data # 获得特征矩阵
y = boston.target # 获得标签
features = boston.feature_names # 获得特征的名称
boston_data = pd.DataFrame(X,columns=features)
boston_data["Price"] = y
boston_data.head()
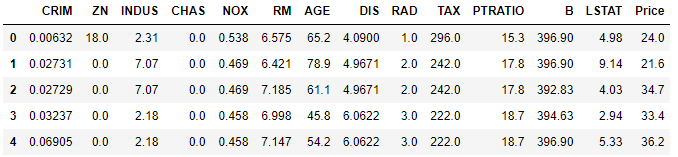
接下来是模型训练和预测可视化
首先我们使用LSTAT列的数据作为要训练的数据,查看它的统计信息
# 统计分析
boston_data["LSTAT"].describe()
count 506.000000
mean 12.653063
std 7.141062
min 1.730000
25% 6.950000
50% 11.360000
75% 16.955000
max 37.970000
Name: LSTAT, dtype: float64
以LSTAT列的数据作为训练集,然后根据该列的数据统计信息,构建测试数据,plot拟合曲线
train = np.reshape(boston_data["LSTAT"].values,(len(boston_data["LSTAT"]),1))
test = np.linspace(0, 38, 506)[:, np.newaxis]
然后分别取 K = 1 , 3 , 5 , 8 , 10 , 40 , 100 , 250 , 506 K=1,3,5,8,10,40,100,250,506 K=1,3,5,8,10,40,100,250,506查看回归效果,KNeighborsRegressor函数官网介绍
from sklearn.neighbors import KNeighborsRegressor
# Fit regression model
# 设置多个k近邻进行比较
n_neighbors = [1, 3, 5, 8, 10, 40,100,250,506]
# 设置图片大小
plt.figure(figsize=(20,10))
for i, k in enumerate(n_neighbors):
# 默认使用加权平均进行计算predictor
clf = KNeighborsRegressor(n_neighbors=k, p=2, metric="minkowski")
# 训练
clf.fit(T, y)
# 预测
y_ = clf.predict(test)
plt.subplot(3, 3, i + 1)
plt.scatter(T, y, color='red', label='data')
plt.plot(test, y_, color='navy', label='prediction')
plt.axis('tight')
plt.legend()
plt.title("KNeighborsRegressor (k = %i)" % (k))
plt.tight_layout()
plt.show()

当
K
=
1
K=1
K=1时,预测结果只与一个样本有关系,从预测曲线中可以看出当k很小时候很容易发生过拟合。
当
K
=
506
K=506
K=506时,预测的结果和最近的506个样本相关,因为我们只有506个样本,此时是所有样本的平均值,此时所有预测值都是均值,很容易发生欠拟合。
同时也可以看到随着K的增大,拟合曲线越光滑。
一般情况下,使用knn的时候,根据数据规模我们会从[3, 20]之间进行尝试,选择最好的k。
2.2 分类任务
分类任务我们使用熟悉的鸢尾花数据集
# 使用莺尾花数据集的前两维数据,便于数据可视化
iris = datasets.load_iris()
X = iris.data[:, :2]
y = iris.target
并且对 K = 1 , 3 , 5 , 8 , 10 , 15 K=1,3,5,8,10,15 K=1,3,5,8,10,15进行测试,查看其分类结果
k_list = [1, 3, 5, 8, 10, 15]
h = .02
# 创建不同颜色的画布
cmap_light = ListedColormap(['orange', 'cyan', 'cornflowerblue'])
cmap_bold = ListedColormap(['darkorange', 'c', 'darkblue'])
plt.figure(figsize=(15,14))
# 根据不同的k值进行可视化
for ind,k in enumerate(k_list):
clf = KNeighborsClassifier(k)
clf.fit(X, y)
# 画出决策边界
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
# 根据边界填充颜色
Z = Z.reshape(xx.shape)
plt.subplot(321+ind)
plt.pcolormesh(xx, yy, Z, cmap=cmap_light)
# 数据点可视化到画布
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=cmap_bold,
edgecolor='k', s=20)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.title("3-Class classification (k = %i)"% k)
plt.show()
分类结果如下,不同的颜色代表不同的类别

当
K
K
K较小时,模型分界位置容易受到局部数据的影响,对局部数据敏感。例如
K
=
1
K=1
K=1时,浅蓝块中嵌入了很多小块的深蓝。而当
K
K
K较大时,模型相对来说较鲁棒,预测结果会落入对应的区域中,对局部数据不那么敏感。
2.3 缺失值填充
如果数据集中有空值,空值是不能参与计算的,我们需要进行数据预处理对空值进行填充,此时我们可以使用KNNImputer进行空值填充。下面我们来看其填充原理:
首先我们构建一个有缺失值的数据
X = [[1, 2, np.nan], [3, 4, 3], [np.nan, 6, 5], [8, 8, 7]]
对其进行空值填充时且设定
K
=
2
K=2
K=2,对于第一个有空值的样本
[
1
,
2
,
n
p
.
n
a
n
]
[1,2,np.nan]
[1,2,np.nan],它的第三维有空值,而与它最近的两个样本是
[
3
,
4
,
3
]
[3,4,3]
[3,4,3]和
[
n
p
.
n
a
n
,
6
,
5
]
[np.nan,6,5]
[np.nan,6,5],它们的第三维的值分别为3和5,用这两个的均值作为填充值,因此填充后为
[
1
,
2
,
4
]
[1,2,4]
[1,2,4]。对于有空值的第二个样本
[
n
p
.
n
a
n
,
6
,
5
]
[np.nan,6,5]
[np.nan,6,5],与其距离最近的两个样本是
[
3
,
4
,
3
]
[3,4,3]
[3,4,3]和
[
8
,
8
,
7
]
[8,8,7]
[8,8,7],第一维缺失值的空值用同样方法填充为
[
5.5
,
6
,
5
]
[5.5,6,5]
[5.5,6,5]。
我们来看代码实现:
# kNN数据空值填充
from sklearn.impute import KNNImputer
imputer = KNNImputer(n_neighbors=2, metric='nan_euclidean')
imputer.fit_transform(X)
array([[1. , 2. , 4. ],
[3. , 4. , 3. ],
[5.5, 6. , 5. ],
[8. , 8. , 7. ]])
有空值的欧式距离又是如何计算的呢?
对于正常样本
[
3
,
4
,
3
]
[3,4,3]
[3,4,3]和
[
8
,
8
,
7
]
[8,8,7]
[8,8,7],计算其欧式距离为:
(
3
−
8
)
2
+
(
4
−
8
)
2
+
(
3
−
7
)
2
=
33
=
7.55
\sqrt{(3-8)^2+(4-8)^2+(3-7)^2}=\sqrt{33}=7.55
(3−8)2+(4−8)2+(3−7)2=33=7.55因此这两个样本的欧氏距离为7.55。
对于有缺失值的样本
[
1
,
2
,
n
p
.
n
a
n
]
[1,2,np.nan]
[1,2,np.nan]和
[
n
p
.
n
a
n
,
6
,
5
]
[np.nan,6,5]
[np.nan,6,5],计算欧式距离只计算没有缺失值的维度的值,并按比例增加其余坐标的权重:
3
1
×
(
2
−
6
)
2
=
48
=
6.93
\sqrt{\frac{3}{1} \times (2-6)^2}=\sqrt{48}=6.93
13×(2−6)2=48=6.93因此这两个样本的欧氏距离为6.93。
用代码计算计算 X X X和 Y Y Y中每对样本之间的欧式距离,如果 Y = N o n e Y=None Y=None则令 Y = X Y=X Y=X,在计算一对样本之间的距离时,此公式将忽略两个样本中任一值均缺失的要素坐标,并按比例增加其余坐标的权重:
from sklearn.metrics.pairwise import nan_euclidean_distances
X = [[np.nan, 6, 5], [3, 4, 3]]
Y = [[3, 4, 3], [1, 2, np.nan], [8, 8, 7]]
nan_euclidean_distances(X, Y)
array([[3.46410162, 6.92820323, 3.46410162],
[0. , 3.46410162, 7.54983444]])





















 340
340











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








