C++正整数因式分解输出表达式

最新推荐文章于 2024-03-07 13:28:47 发布

子奕°

最新推荐文章于 2024-03-07 13:28:47 发布

阅读量3.3k

点赞数 4

分类专栏：算法

本文链接：https://blog.csdn.net/kcyxws/article/details/115350796

版权

算法专栏收录该内容

1 篇文章

订阅专栏

题目

大于1的正整数n可以分解为：
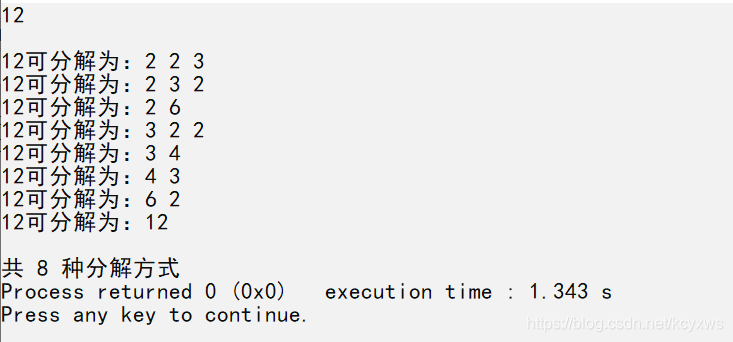
在这里插入图片描述

当n=12时，共有8种不同的分解式：
在这里插入图片描述

对于给定的正整数n，编程计算n共有多少种不同的分解式，并输出响应分解式子。
输入
数据有多行，给出正整数n（1≤n≤2000000000）。
输出
正整数n的不同的分解式数量，以及分解式。

代码

#include <iostream>
#include <vector>
using namespace std;
vector <int> factor;
int total=0;
int num;
void output()
{
    vector<int>::iterator v;
    v = factor.begin();
    while(v!=factor.end())
    {
        cout<<*v<<" ";
        v++;
    }
    cout<<endl;
}
void solve(int n)
{
    if(n == 1)
    {
        total++;
        cout<<num<<"可分解为：";
        output();//输出向量中的元素
    }
    else
        for(int i = 2; i <= n; i++)
            if (n % i == 0)
            {
                //如果i是n的因子，则将i压入栈
                factor.push_back(i);
                solve(n / i);
                factor.pop_back();
            }
}

int main()
{
    cin>>num;
    cout<<endl;
    solve(num);
    cout<<endl;
    cout<<"共 "<<total<<" 种分解方式";
    return 0;
}