目录
1.算法解释

还有一些前置理论,基础的思想以前写过:从递归到动态规划,详细解析_chy响当当的博客-CSDN博客_递归转动态规划
2.基本动态规划:一维
(1)70. Climbing Stairs (Easy)
题解
这是十分经典的斐波那契数列题。定义一个数组 dp , dp[i] 表示走到第 i 阶的方法数。因为我们每次可以走一步或者两步,所以第 i 阶可以从第 i-1 或 i-2 阶到达。换句话说,走到第 i 阶的 方法数即为走到第 i-1 阶的方法数加上走到第 i-2 阶的方法数。这样我们就得到了状态转移方程 dp[i] = dp[i-1] + dp[i-2]。注意边界条件的处理。
int climbStairs(int n) {
if (n <= 2) return n;
vector<int> dp(n + 1, 1);
for (int i = 2; i <= n; ++i) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}压缩空间的话:
int climbStairs(int n) {
if (n <= 2) return n;
int pre2 = 1, pre1 = 2, cur;
for (int i = 2; i < n; ++i) {
cur = pre1 + pre2;
pre2 = pre1;
pre1 = cur;
}
return cur;
}(2)198打家劫舍

初始化dp[1]别忘了
//,dp[i] 表示抢劫到第 i 个房子时,可以抢劫的最大数量 //本题的状态转移方程为 dp[i] = max(dp[i-1],nums[i - 1] + dp[i - 2])。 int rob(vector<int>& nums) { if (nums.empty()) return 0; int n = nums.size(); vector<int> dp(n + 1, 0); dp[1] = nums[0]; for (int i = 2; i <= n; ++i) { dp[i] = max(dp[i - 1], nums[i - 1] + dp[i - 2]); } return dp[n]; } //压缩空间版: int rob(vector<int>& nums) { if (nums.empty()) return 0; int n = nums.size(); if (n == 1) return nums[0]; int pre2 = 0, pre1 = 0, cur; for (int i = 0; i < n; ++i) { cur = max(pre2 + nums[i], pre1); pre2 = pre1; pre1 = cur; } return cur; }
(3)413等差数列划分


//求和求和!
class Solution {
public:
//dp[i]代表以i结尾的数组有多少个等差数列子数组
//转移方程
//而等差子数组可以在任意一个位置终结,因此此题在最后需要对 dp 数组求和。
int numberOfArithmeticSlices(vector<int>& nums) {
int n = nums.size();
vector<int> dp(n, 0);
if (n <= 2) {
return 0;
}
for (int i = 2; i <n; ++i) {
if (nums[i] - nums[i - 1] == nums[i - 1] - nums[i - 2]) {
dp[i] = dp[i - 1] + 1;
}
}
return accumulate(dp.begin(), dp.end(), 0);
}
};
//还有一个找规律
/*仔细观察,会发现当整个数组为(1, 2, 3, 4, 5, 6)的时候,我们先取出前三个,(1, 2, 3)的等差数列的个数为1,
(1, 2, 3, 4)的等差数列的个数为3,(1, 2, 3, 4, 5)的等差数列的个数为6,
(1, 2, 3, 4, 5, 6)的等差数列个数为10,
以此类推我们可以很容易的发现在一个等差数列中加入一个数字,如果还保持着等差数列的特性,
每次的增量都会加1,你看这个1是指1-》3加2,3-》6加3,6-》10加4
如果刚加进来的数字与原先的序列构不成等差数列,就将增量置为0,接下来继续循环,*/
/*
int numberOfArithmeticSlices(int []A) {
if (A == NULL || A.length <= 2)
return 0;
int res = 0;
int add = 0;
for (int i = 2; i < A.length; i++)
if (A[i - 1] - A[i] == A[i - 2] - A[i - 1])
res += ++add;
else
add = 0;
return res;
}*/3.基本动态规划:二维
(1)64最小路径和
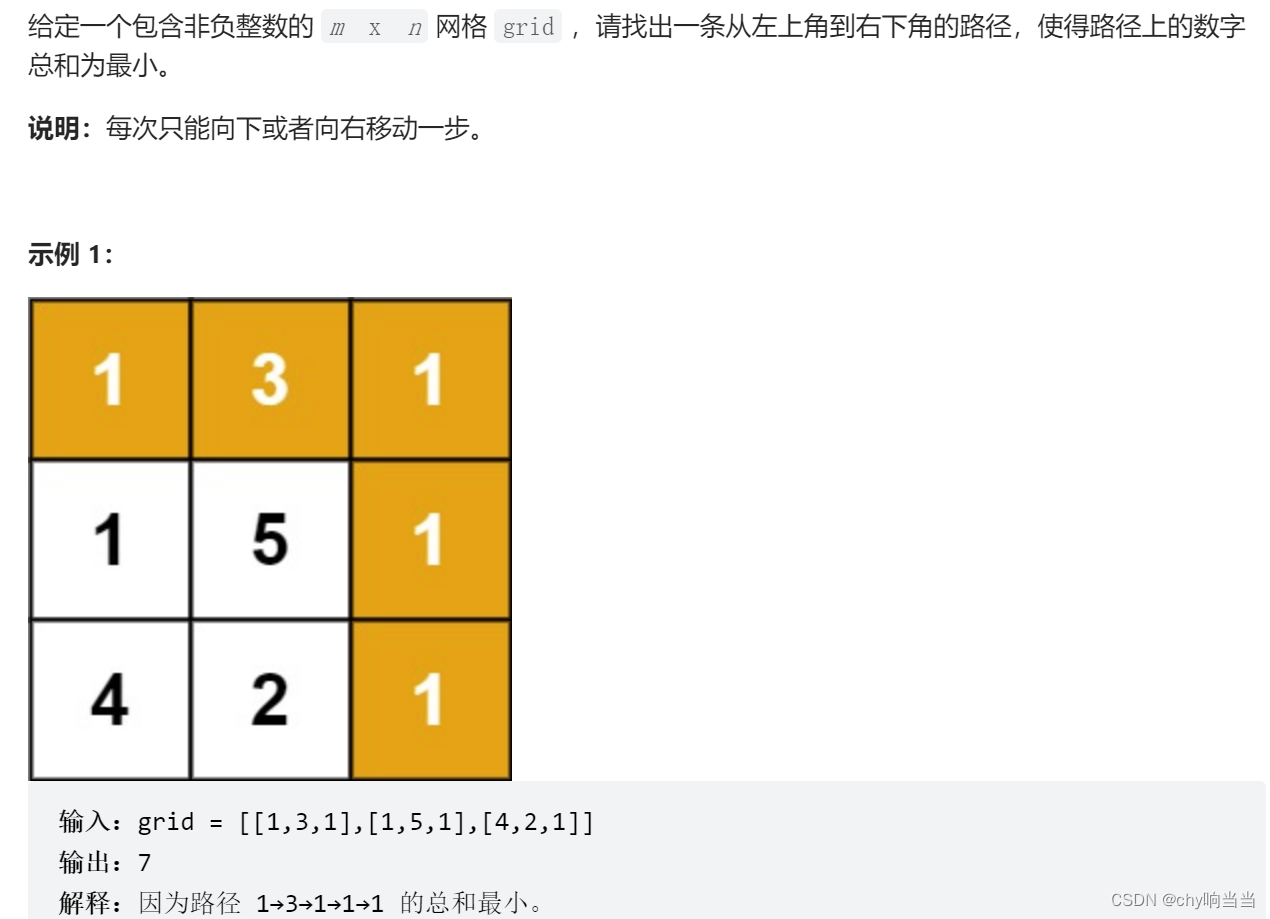
我们可以定义一个同样是二维的 dp 数组,其中 dp[i][j] 表示从左上角开始到 (i, j) 位置的最优路径的数字和。因为每次只能向下或者向右移动,我们可以很容易得到状态转移方程 dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j],其中 grid 表示原数组
class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
int r = grid.size();
int c = grid[0].size();
vector<vector<int>>dp(r, vector<int>(c, 0));
for (int i = 0; i < r; ++i) {
for(int j=0;j<c;++j){
//边界特殊情况要考虑好哦
if (i == 0 && j == 0) {
dp[i][j] = grid[i][j];
}
else if (i == 0) {
dp[i][j] = dp[i][j - 1] + grid[i][j];
}
else if (j == 0) {
dp[i][j] = dp[i - 1][j] + grid[i][j];
}
else {
dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
}
}
}
return dp[r - 1][c - 1];
}
};
int minPathSum(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
vector<int> dp(n, 0);
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (i == 0 && j == 0) {
dp[j] = grid[i][j];
}
else if (i == 0) {
dp[j] = dp[j - 1] + grid[i][j];
}
else if (j == 0) {
dp[j] = dp[j] + grid[i][j];
}
else {
dp[j] = min(dp[j], dp[j - 1]) + grid[i][j];
}
}
}
return dp[n - 1];
}(2)542 0-1矩阵


法一,广度:
//第一反应,广搜
//48/50超时,优化一下应该可以过,
//优化方法一:就是把0的位置加入队列,然后从零开始向外搜1,而不是遍历矩阵,从1搜0
//方法二:visit防止重复访问,这个还是不太行
class Solution {
public:
vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
int r = mat.size();
int c = mat[0].size();
vector<vector<int>> rs(r, vector<int>(c, 0));
vector<vector<bool>> visited(r, vector<bool>(c, 0));
for(int i = 0; i < r; ++i) {
for (int j = 0; j < c; ++j) {
if (mat[i][j] == 0)continue;
if (visited[i][j]) continue;
visited[i][j] = true;
queue<vector<int>> qq;
qq.push({ i + 1,j });
qq.push({ i - 1,j });
qq.push({ i ,j - 1});
qq.push({ i ,j+ 1 });
int len = 0;
while (!qq.empty()) {
int circle_num = qq.size();
++len;
bool flag = false;
while (circle_num--) {
vector<int> front = qq.front();
qq.pop();
int x = front[0];
int y = front[1];
if (x < 0 || y < 0 || x >= r || y >= c) {
continue;
}
if (mat[x][y] == 0) {
flag = true;
break;
}
else {
qq.push({ x+1,y });
qq.push({ x ,y + 1});
qq.push({ x - 1,y });
qq.push({ x,y - 1 });
}
}
if (flag) {
break;
}
}
rs[i][j] = len;
}
}
return rs;
}
};法二,dp
vector<vector<int>> updateMatrix(vector<vector<int>>& matrix) {
if (matrix.empty()) return {};
int n = matrix.size(), m = matrix[0].size();
vector<vector<int>> dp(n, vector<int>(m, INT_MAX - 1));
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
if (matrix[i][j] == 0) {
dp[i][j] = 0;
}
else {
if (j > 0) {
dp[i][j] = min(dp[i][j], dp[i][j - 1] + 1);
}
if (i > 0) {
dp[i][j] = min(dp[i][j], dp[i - 1][j] + 1);
}
}
}
}
for (int i = n - 1; i >= 0; --i) {
for (int j = m - 1; j >= 0; --j) {
if (matrix[i][j] != 0) {
if (j < m - 1) {
dp[i][j] = min(dp[i][j], dp[i][j + 1] + 1);
}
if (i < n - 1) {
dp[i][j] = min(dp[i][j], dp[i + 1][j] + 1);
}
}
}
}
return dp;
}
(3)221最大正方形
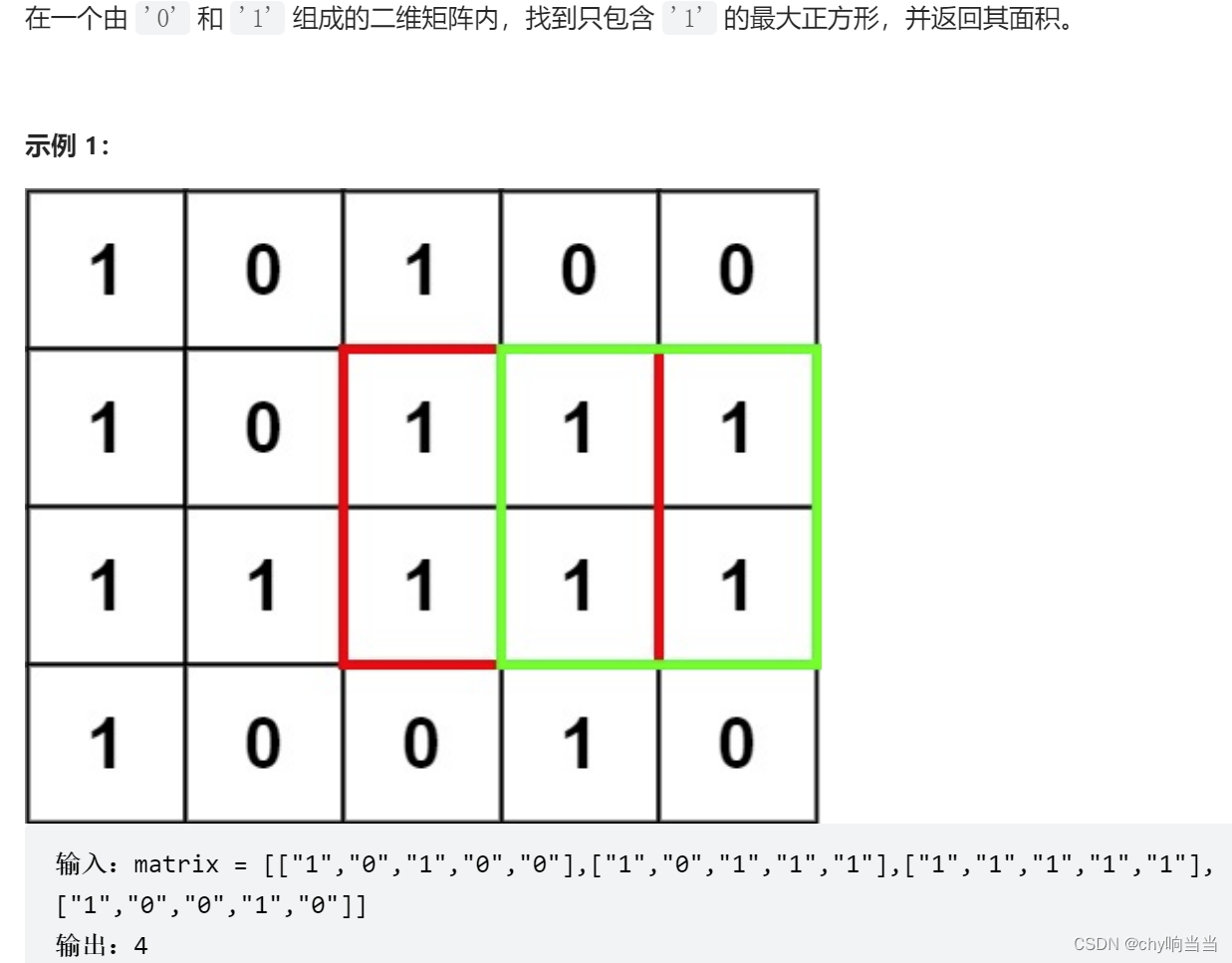
/*当我们判断以某个点为正方形右下角时最大的正方形时,那它的上方,左方和左上方三个点也一定是某个正方形的右下角,
否则该点为右下角的正方形最大就是它自己了。这是定性的判断,那具体的最大正方形边长呢?
我们知道,该点为右下角的正方形的最大边长,最多比它的上方,左方和左上方为右下角的正方形的边长多1,
最好的情况是是它的上方,左方和左上方为右下角的正方形的大小都一样的,这样加上该点就可以构成一个更大的正方形。
但如果它的上方,左方和左上方为右下角的正方形的大小不一样,合起来就会缺了某个角落,
这时候只能取那三个正方形中最小的正方形的边长加1了。
假设dpi表示以i,j为右下角的正方形的最大边长,则有 dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1]) + 1*/
class Solution {
public:
int maximalSquare(vector<vector<char>>& a) {
int r = a.size();
int c = a[0].size();
vector < vector<int>> dp(r+1, vector<int>(c+1,0));//初始化
if (a.empty())return 0;
int max_size = 0;
//
for (int i = 1; i <= r; ++i) {
for (int j = 1; j <= c; ++j) {
if (a[i-1][j-1] == '1') {
dp[i][j] = 1 + min(dp[i - 1][j - 1], min(dp[i][j - 1], dp[i - 1][j]));// 这个min好好体会一下
}
max_size = max(max_size, dp[i][j]);//dpi表示以i,j为右下角的正方形的最大边长!!!!!!!!
}
}
//这里是求边长哦
return max_size * max_size;
}
};
/*
动态规划的小小技巧吧:
默念一句话“动态规划每一步填表都建立在之前已经填完的表上”;
表的值的意义和你return的值的意义一样(不要多想)!!!
不要考虑初始化边缘(千万不要从dp[0][0]想思路!!!),
从中间取一个点,想这个点的值怎么根据它的左边、上边、左上边、左下边的值计算出来!!!*/4.分割问题
(1)279完全平方数


/* dp[i] 表示数字 i 最少可以由几个完全平方数相加
构成。在本题中,位置 i 只依赖 i - k^2 的位置,如 i - 1、i - 4、i - 9 等等,才能满足完全平方分割
的条件。因此 dp[i] 可以取的最小值即为 1 + min(dp[i-1], dp[i-4], dp[i-9] · · · )。*/
class Solution {
public:
int numSquares(int n) {
vector<int> dp(n + 1, INT_MAX);
dp[0] = 0;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j * j <= i; ++j) {//牛逼啊 时间复杂度O(nlogn),空间复杂度O(n)
dp[i] = min(dp[i], dp[i - j * j] + 1);
}
}
return dp[n];
}
};
class Solution {
public:
int numSquares(int n) {
vector<int> dp(n + 1, INT_MAX);
dp[0] = 0;
for (int i = 1; i <= sqrt(n) + 1; ++i) {
for (int j = 0; j <= n; ++j) {
if (j - i * i >= 0) {
dp[j] = min(dp[j], dp[j - i * i] + 1);
}
}
}
return dp[n];
}
};
//还可以用背包
java版本
class Solution {
public int numSquares(int n) {
完全背包
int max = Integer.MAX_VALUE;
int[] dp = new int[n + 1];
for (int i = 1; i < dp.length; ++i) dp[i] = max;
先遍历物品,后遍历背包
for (int i = 1; i * i <= n; ++i) {
for (int j = 1; j <= n; ++j) {
if (j >= i * i) {
dp[j] = Math.min(dp[j], dp[j - i * i] + 1);
}
}
}
先遍历背包,再遍历物品
for (int j = 1; j <= n; ++j) {
for (int i = 1; i * i <= j; ++i) {
dp[j] = Math.min(dp[j], dp[j - i * i] + 1);
}
}
return dp[n];
}
}
(2)解码方法
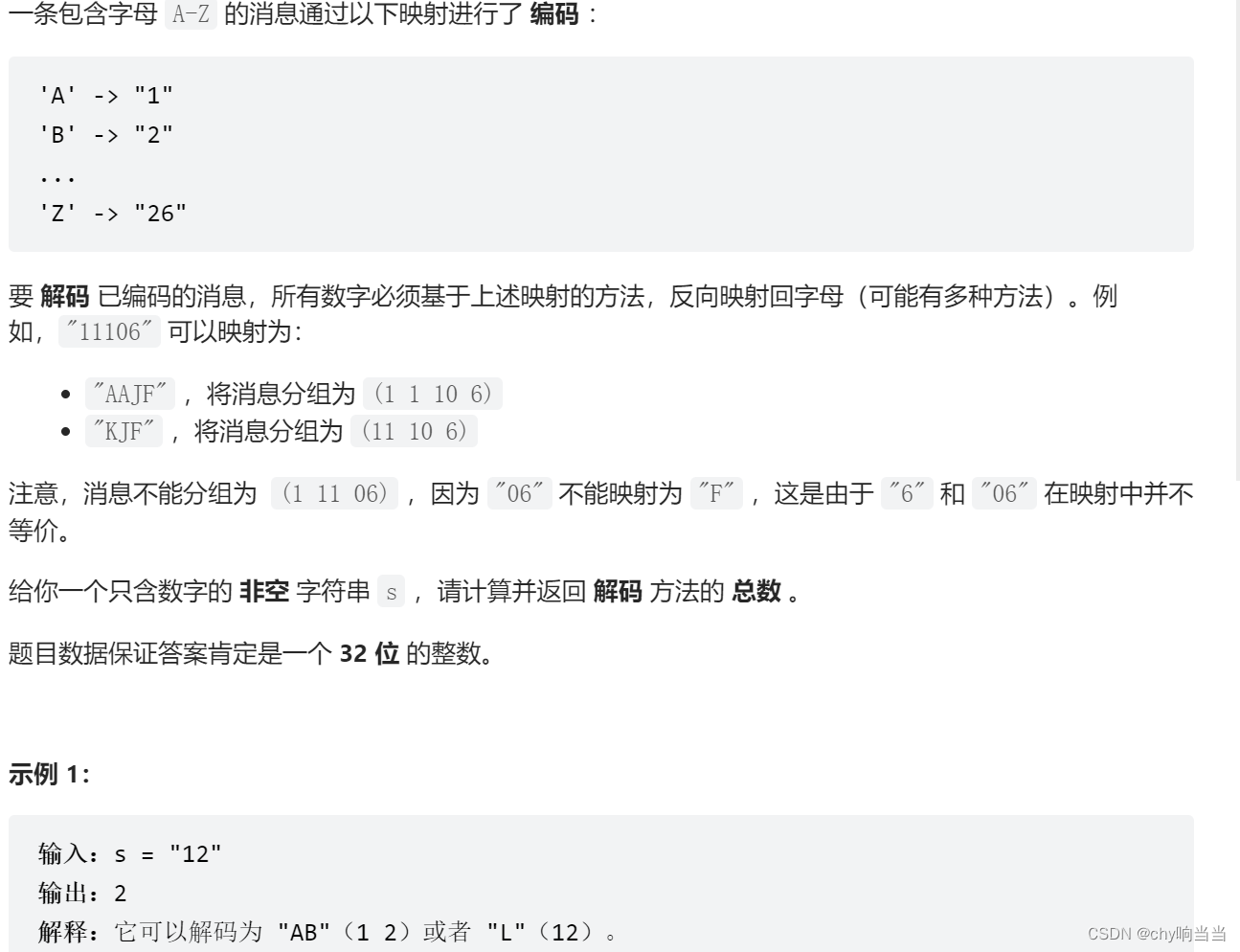
题解:
上楼梯的复杂版?
如果连续的两位数符合条件,就相当于一个上楼梯的题目,可以有两种选法:
1.一位数决定一个字母
2.两位数决定一个字母
就相当于dp(i) = dp[i-1] + dp[i-2];
如果不符合条件,又有两种情况
1.当前数字是0:
不好意思,这阶楼梯不能单独走,
dp[i] = dp[i-2]
2.当前数字不是0
不好意思,这阶楼梯太宽,走两步容易扯着步子,只能一个一个走
dp[i] = dp[i-1];
//怎么类比楼梯呢?你想想如果s[i]是要单独算的,那就是上一阶台阶 dp[i]+=dp[i-1] //如果s[i]可以作为两位数的末位,那就是上两阶台阶 dp[i]+=dp[i-2] //太牛了好好体会一下 class Solution { public: int numDecodings(string s) { int n = s.size(); if (n == 0) { return 0; } int prev = s[0] - '0'; if (!prev) return 0;//防止0开头 if (n == 1) return 1; vector<int> dp(n+1,0); dp[0] = 1; dp[1] = 1;//初始化,想想看为什么 //在把特殊情况排除之后,剩下的都是正常的,你for里面又是从2开始,那dp[1]必须得为1,那dp0为什么为1呢? //因为进去之后要用到dp[2-2],那也为1才行 for (int i = 2; i <= n; ++i) { int cur = s[i - 1] - '0'; if ((prev == 0 || prev > 2) && cur == 0) { return 0;//防止02 37这两种情况 } if ((prev < 2 && prev > 0) || prev == 2 && cur < 7) { if (cur) { dp[i] = dp[i - 2] + dp[i - 1]; } else { dp[i] = dp[i - 2];//cur=0必须跟在后面一起算 } } else { dp[i] = dp[i - 1];//只能单个算 } prev = cur;//cur到pre,真的妙 } return dp[n]; } };
(3)139单词拆分(重点)

类似于完全平方数分割问题,这道题的分割条件由集合内的字符串决定,因此在考虑每个分割位置时,需要遍历字符串集合,以确定当前位置是否可以成功分割。注意对于位置 0 ,需要初始化值为真
其实这个算背包问题,完全背包
//标答2,这个好理解 递推公式是 if([j, i] 这个区间的子串出现在字典里 && dp[j]是true) 那么 dp[i] = true。
class Solution {
public:
bool wordBreak(string s, vector<string>& wordDict) {
unordered_set<string> wordSet(wordDict.begin(), wordDict.end());
vector<bool> dp(s.size() + 1, false);
dp[0] = true;//0一定要为1,不然后面都是false了
//i j 一个从 一个从0,i是因为要dp1-n,而且截取长度也是从1开始而不是从0,j就简单了是正常0开始的,反正要小心一点
for (int i = 1; i <= s.size(); i++) { // 遍历背包
for (int j = 0; j < i; j++) { // 遍历物品
string word = s.substr(j, i - j); //substr(起始位置,截取的个数)
if (wordSet.find(word) != wordSet.end() && dp[j]) {
dp[i] = true;
}
}
}
return dp[s.size()];
}
};
//标答1
bool wordBreak(string s, vector<string>& wordDict) {
int n = s.length();
vector<bool> dp(n + 1, false);
dp[0] = true;
unordered_set<string> m(wordDict.begin(), wordDict.end());//去重的
for (int i = 1; i <= n; ++i) {
for (const string& word : m) {//加快速度
int len = word.length();
if (i >= len && s.substr(i - len, len) == word) {
dp[i] = dp[i] || dp[i - len];
}
}
}
return dp[n];
}5. 子序列问题
(1)300最长递增子序列

注意这里是不连续的


class Solution {
public:
//n^2
//递推没想明白
/*对于每一个位置 i,如果其之前的某
个位置 j 所对应的数字小于位置 i 所对应的数字,则我们可以获得一个以 i 结尾的、长度为 dp[j]
+ 1 的子序列*/
int lengthOfLIS(vector<int>& nums) {
int max_length = 0, n = nums.size();
if (n <= 1) return n;
vector<int> dp(n, 1);
for (int i = 0; i < n; ++i) {
for (int j = 0; j < i; ++j) {
if (nums[i] > nums[j]) {
dp[i] = max(dp[i], dp[j] + 1);
}
}
max_length = max(max_length, dp[i]);
}
return max_length;
}
};
//法二 nlogn
//其实是在动态规划的基础上用了贪心
/**
dp[i]: 所有长度为i+1的递增子序列中, 最小的那个序列尾数.
由定义知dp数组必然是一个递增数组, 可以用 maxL 来表示最长递增子序列的长度.
对数组进行迭代, 依次判断每个数num将其插入dp数组相应的位置:
1. num > dp[maxL], 表示num比所有已知递增序列的尾数都大, 将num添加入dp
数组尾部, 并将最长递增序列长度maxL加1
2. dp[i-1] < num <= dp[i], 只更新相应的dp[i]
**/
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
int n = nums.size();
int max_size = 0;
vector<int>dp(n, 0);
for (const int &num : nums) {
//二分查找
int low = 0;
int high = max_size;
while (low < high) {
int mid = (low + high) / 2;
if (dp[mid] < num) {
low = mid + 1;
}
else {
high = mid;
}
}
if (low == max_size) {//说明比dp里面的都大
dp[max_size++] = num;
}
else {//说明有一个可以替换
dp[low] = num;
}
}
return max_size;
}
};
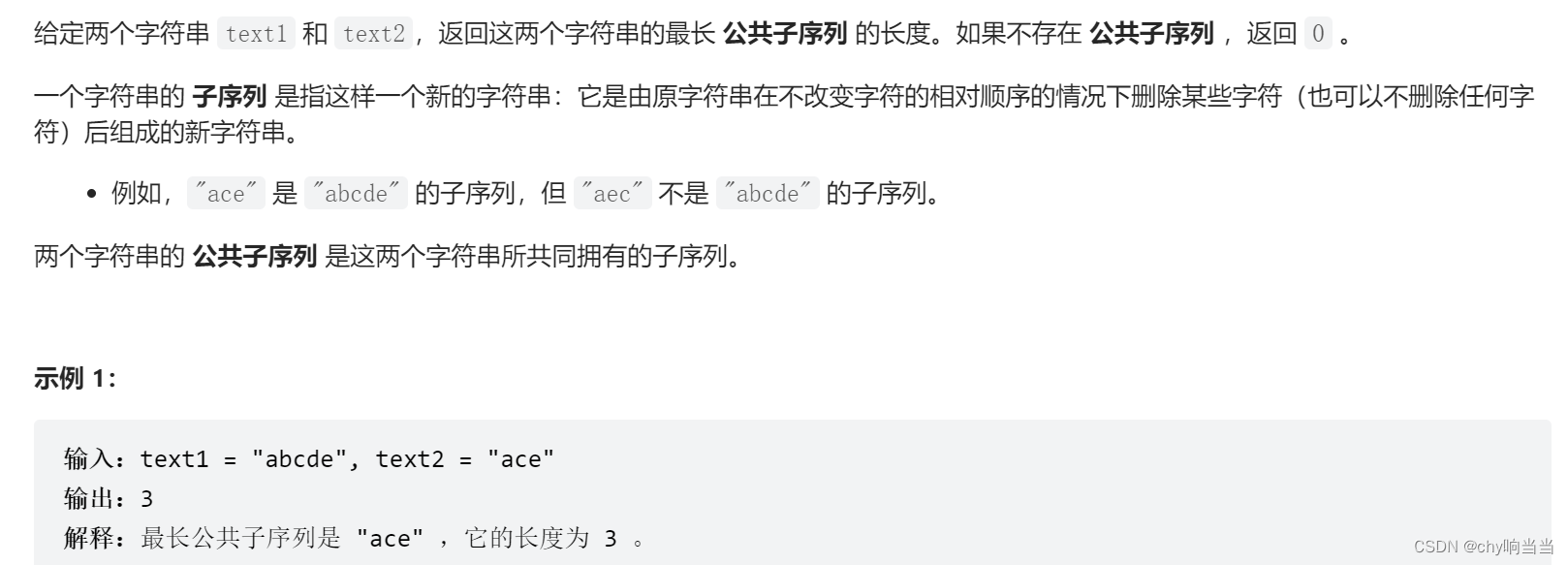
(2)1143. 最长公共子序列

class Solution {
public:
/* dp[i][j] 表示到第一个字符串位置 i 为止、到
第二个字符串位置 j 为止、最长的公共子序列长度。*/
int longestCommonSubsequence(string t1, string t2) {
int n = t1.length();
int m = t2.length();
vector<vector<int>> dp(n+1, vector<int>(m+1, 0));
/* if (n == 0 || m == 0) {
return 0;
}
if (n == 1) {
if (t2.find(t1) != t2.npos) {
return 1;
}
return 0;
}
if (m == 1) {
if (t1.find(t1) != t1.npos) {
return 1;
}
return 0;
} 这些判断不用写,想想看为什么
*/
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j) {
if (t1[i - 1] == t2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
}
else {
dp[i][j] = max(dp[i-1][j], dp[i ][j - 1]);//这个很关键我写错了、
/* dp[i][j] = Math.max(dp[i - 1][j], dp[i][j]);
dp[i][j] = Math.max(dp[i][j - 1], dp[i][j]); 或者这样写更理解*/
}
}
}
return dp[n][m];
}
};6.背包问题

01背包


完全背包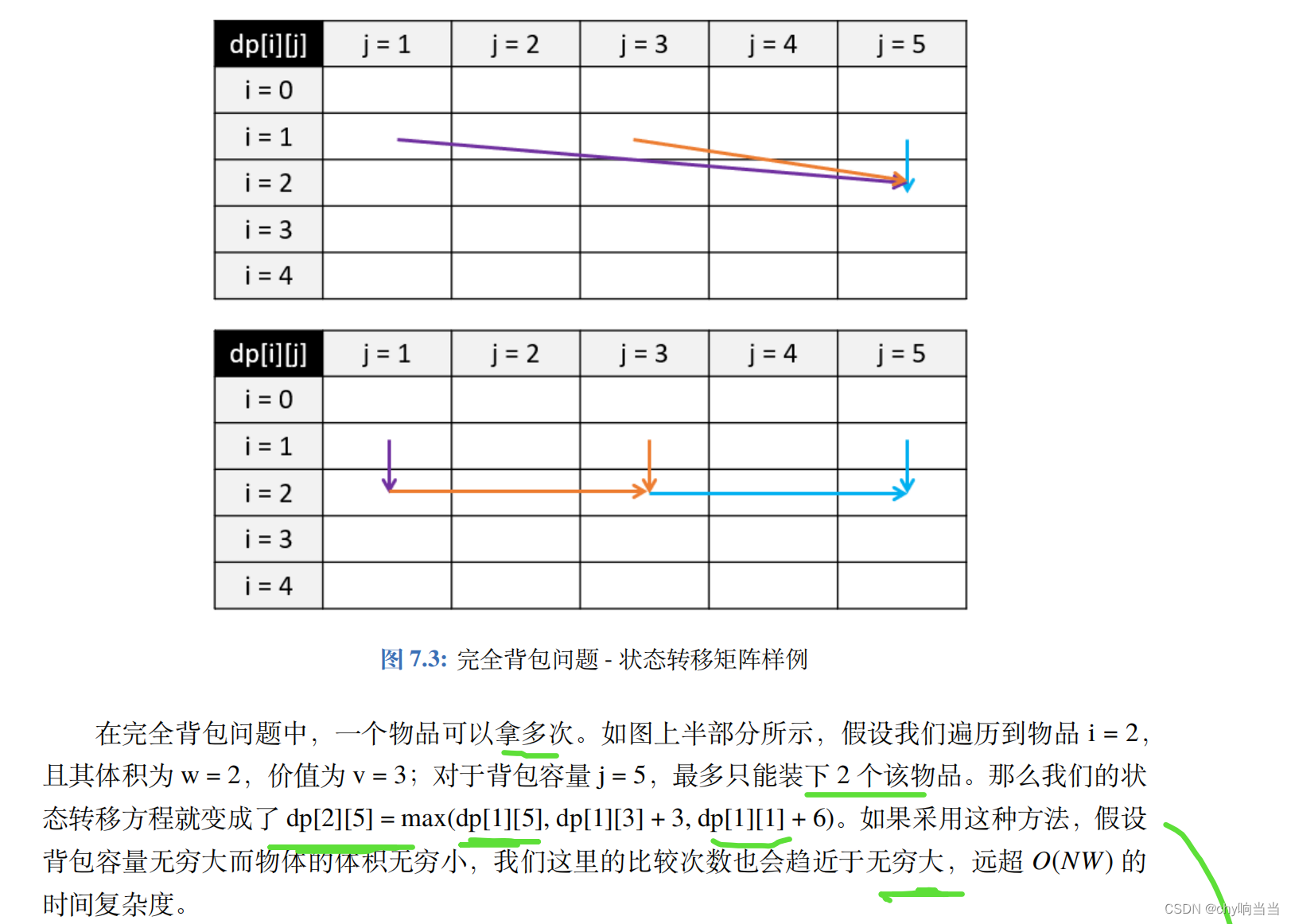

同样的,我们也可以利用空间压缩将时间复杂度降低为 O ( W ) 。这里要注意我们在遍历每一行的时候必须 正向遍历 ,因为我们需要利用当前物品在第 j-w 列的信息

综合模板

1
、
0/1
背包:外循环
nums,
内循环
target,target
倒序且target>=nums[i];
2
、完全背包(组合):外循环
nums,
内循环
target ,target正序且
target>=nums[i];
3
、完全背包(排列):外循环
target,
内循环
nums ,target正序且
target>=nums[i
】
(1)416分割等和子集

/*本题等价于 0-1 背包问题,设所有数字和为 sum,我们的目标是选取一部分物品,使得它们
的总和为 sum/2。这道题不需要考虑价值,因此我们只需要通过一个布尔值矩阵来表示状态转移
矩阵。注意边界条件的处理。*/
//不会啊啊
class Solution {
public:
//和是容量
//w是nums【i]
bool canPartition(vector<int>& nums) {
int sum = accumulate(nums.begin(), nums.end(), 0);
if (sum & 1) return false;
int target = sum / 2, n = nums.size();
vector<vector<bool>> dp(n + 1, vector<bool>(target + 1, false));
for (int i = 0; i <= n; ++i) {
dp[i][0] = true;
}
for (int i = 1; i <= n; ++i) {
for (int j = 0; j <= target; ++j) {
if (j - nums[i - 1] >= 0) {
dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i - 1]];//这里max其实就是转化为||了
}
else {
dp[i][j] = dp[i - 1][j];
}
}
}
return dp[n][target];
}
//空间压缩
bool canPartition2(vector<int>& nums) {
int sum = accumulate(nums.begin(), nums.end(), 0);
if (sum & 1) return false;
int target = sum / 2, n = nums.size();
vector<bool> dp(target + 1, false);
//关键:
dp[0] = true;//不然进行不下去的
for (int i = 1; i <= n; ++i) {
for (int j = target; j >=0; --j) {//逆向
if (j - nums[i - 1] >= 0) {
dp[j] = dp[j] || dp[j - nums[i - 1]];//这里max其实就是转化为||了
}
else {
dp[j] = dp[j];
}
}
}
return dp[target];
}
};(2)322零钱兑换

//完全背包问题
//标答1,它这个外层背包,内层硬币
int coinChange(vector<int>& coins, int amount) {
if (coins.empty()) return -1;
vector<int> dp(amount + 1, amount + 2);
dp[0] = 0;
for (int i = 1; i <= amount; ++i) {
for (const int& coin : coins) {
if (i >= coin) {
dp[i] = min(dp[i], dp[i - coin] + 1);
}
}
}
return dp[amount] == amount + 2 ? -1 : dp[amount];
}
//标答2
//由于这里不强调排列和组合,所以外层硬币也可以
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
vector<int> dp(amount + 1, INT_MAX);
dp[0] = 0;
for (int i = 0; i < coins.size(); i++) { // 遍历物品
for (int j = coins[i]; j <= amount; j++) { // 遍历背包
if (dp[j - coins[i]] != INT_MAX) { // 如果dp[j - coins[i]]是初始值则跳过
dp[j] = min(dp[j - coins[i]] + 1, dp[j]);
}
}
}
if (dp[amount] == INT_MAX) return -1;
return dp[amount];
}
};
//我的
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
//容量是amount
//w是conis[i]
//value其实不需要,跟416一样
int n = coins.size();
vector<vector<int>> dp(n+1, vector<int>(amount+1, amount + 2));//因为要MIn所以要初始化最大值
for (int i = 0; i <= n; ++i) {
dp[i][0] = 0;//这个0很重要,不然全部不执行。
}
//经验:初始化真的要做好
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= amount; ++j) {//这样写一定要从1开始
if (j >= coins[i-1]) {
dp[i][j] = min(dp[i - 1][j], dp[i][j - coins[i - 1]] + 1);
}
else {
dp[i][j] = dp[i - 1][j];
}
}
}
return dp[n][amount] == amount + 2 ? -1 : dp[n][amount];
}
};
//按标答2的优化,循环的起始,循环体内部,真的暂时只能体会,我还没水平说出所以然
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
//容量是amount
//w是conis[i]
//value其实不需要,跟416一样
int n = coins.size();
vector<int> dp(amount + 1, amount + 2);//因为要MIn所以要初始化最大值
dp[0] = 0;//这个0很重要,不然全部不执行。
//经验:初始化真的要做好
for (int i = 1; i <= n; ++i) {
for (int j = coins[i - 1]; j <= amount; ++j) {
if (dp[j - coins[i - 1]] != amount + 2) {
dp[j] = min(dp[j], dp[j - coins[i - 1]] + 1);
}
}
}
return dp[amount] == amount + 2 ? -1 : dp[amount];
}
};
//按标答1的优化
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
//容量是amount
//w是conis[i]
//value其实不需要,跟416一样
int n = coins.size();
vector<int> dp(amount + 1, amount + 2);//因为要MIn所以要初始化最大值
dp[0] = 0;//这个0很重要,不然全部不执行。
//经验:初始化真的要做好
for (int i = 1; i <= n; ++i) {
for (int j = coins[i - 1]; j <= amount; ++j) {
if (j >= coins[i - 1]) {
dp[j] = min(dp[j], dp[j - coins[i - 1]] + 1);
}
else {
dp[j] = dp[j - 1];
}
}
}
return dp[amount] == amount + 2 ? -1 : dp[amount];
}
};(3)一和零

//这个通过模仿416终于会做了
class Solution {
public:
//len个物品
//容量为m个0 n个1,好像要三维?
//所以i-1这一条直接就是压缩掉
int findMaxForm(vector<string>& strs, int m, int n) {
int len = strs.size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
for (int i = 0; i < len; ++i) {
int one = 0;
int zero = strs[i].size();
while (strs[i].find("1") != strs[i].npos) {
++one;
--zero;
int pos = strs[i].find("1");
strs[i].erase(pos, 1);
}
//01背包,压缩后逆序
for (int j = m; j >= 0; --j) {
for (int k = n; k >= 0; --k) {
if (j >= zero && k >= one) {
dp[j][k] = max(dp[j][k], dp[j - zero][k - one] + 1);
}
/*
//这一段是错的,你一个字符串要么都算要么就都不算,不能拆开来的
else if (j >= zero) {
dp[j][k] = max(dp[j][k], dp[j - zero][k] + 1);
}
else if (k >= one) {
dp[j][k] = max(dp[j][k], dp[j][k - one] + 1);
}*/
else {
dp[j][k] = dp[j][k];
}
}
}
}
return dp[m][n];
}
};7. 字符串编辑
(1)72编辑距离

题解
类似于题目 1143 ,我们使用一个二维数组 dp[i][j] ,表示将第一个字符串到位置 i 为止,和第二个字符串到位置 j 为止,最多需要几步编辑。当第 i 位和第 j 位对应的字符相同时, dp[i][j] 等于 dp[i-1][j-1] ;当二者对应的字符不同时,修改的消耗是 dp[i-1][j-1]+1 ,插入 i 位置 / 删除 j 位置的消耗是 dp[i][j-1] + 1 ,插入 j 位置 / 删除 i 位置的消耗是 dp[i-1][j] + 1 。
/*,我们使用一个二维数组 dp[i][j],表示将第一个字符串到位置 i 为止,和第
二个字符串到位置 j 为止,最多需要几步编辑。当第 i 位和第 j 位对应的字符相同时,
dp[i][j] 等 于 dp[i-1][j-1];当二者对应的字符不同时,修改的消耗是 dp[i-1][j-1]+1,
插入 i 位置/删除 j 位置的消耗是 dp[i][j-1] + 1,插入 j 位置/删除 i 位置的消耗是 dp[i-1][j] + 1。*/
class Solution {
public:
int minDistance(string word1, string word2) {
int m = word1.length(), n = word2.length();
vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
for (int i = 0; i <= m; ++i) {
for (int j = 0; j <= n; ++j) {
if (i == 0) {
dp[i][j] = j;//就是不断插入
}
else if (j == 0) {
dp[i][j] = i;
}
else {
//这一步增删改的min真的太牛逼了,好好体会一下,确实我们是从我w1转化为w2,
//但是w1删其实就相当于w2增,操作数都是一样的
dp[i][j] = min(
dp[i - 1][j - 1] + ((word1[i - 1] == word2[j - 1]) ? 0 : 1),
min(dp[i - 1][j] + 1, dp[i][j - 1] + 1));
}
}
}
return dp[m][n];
}
};(2)650只有两个键的键盘
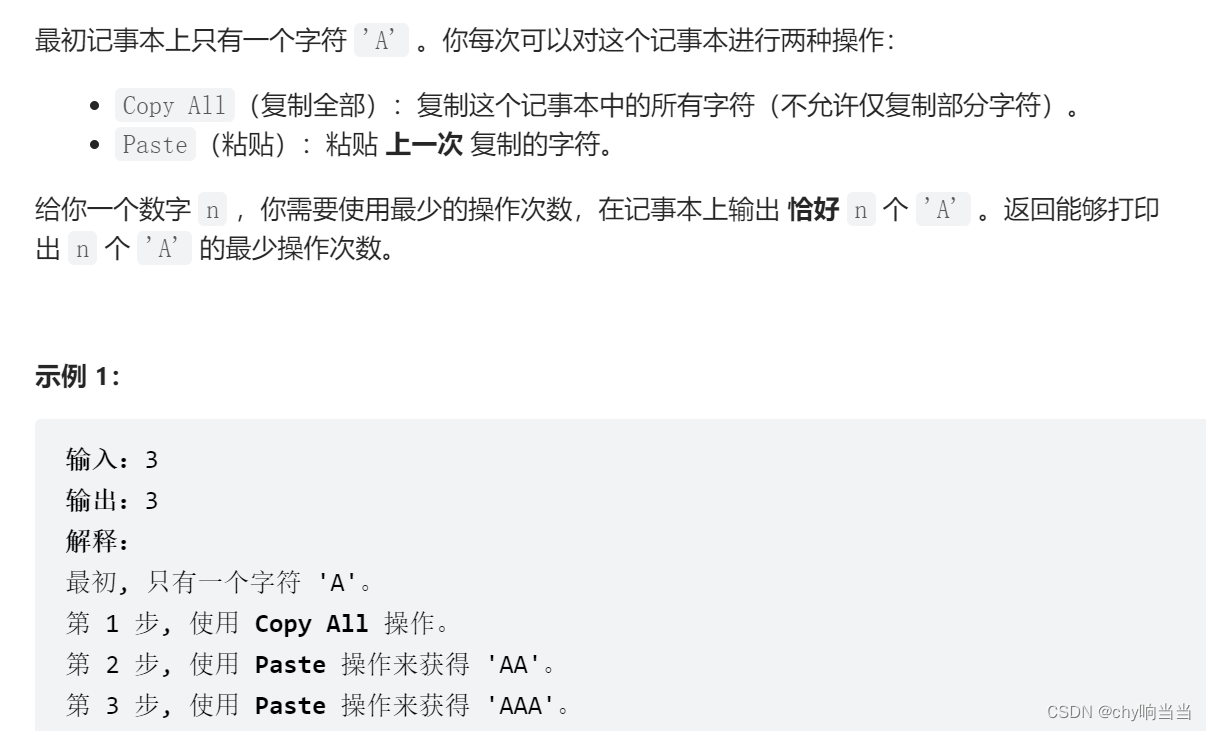
题解不同于以往通过加减实现的动态规划,这里需要乘除法来计算位置,因为粘贴操作是倍数增加的。我们使用一个一维数组 dp ,其中位置 i 表示延展到长度 i 的最少操作次数。对于每个位置 j,如果 j 可以被 i 整除,那么长度 i 就可以由长度 j 操作得到,其操作次数等价于把一个长度为 1 的 A 延展到长度为 i/j 。因此我们可以得到递推公式 dp[i] = dp[j] + dp[i/j]
这里为什么你不 是i/j而是dp[i/ j]你可以想, 比如i/j=8,那 么真的是加八吗 ?这个八完全可 以通过变成4再 乘以2得到,这 样次数就比8小 了。
class Solution {
public:
int minSteps(int n) {
vector<int> dp(n + 1);
int h = sqrt(n);
for (int i = 2; i <= n; ++i) {
dp[i] = i;
for (int j = 2; j <= h; ++j) {
if (i % j == 0) {
dp[i] = dp[j] + dp[i / j];//这个dp[i/j]很关键!!!
break;
}
}
}
return dp[n];
}
};(3)10正则匹配

题解
我们可以使用一个二维数组 dp ,其中 dp[i][j] 表示以 i 截止的字符串是否可以被以 j 截止的正则表达式匹配。根据正则表达式的不同情况,即字符、星号,点号,我们可以分情况讨论来更 新 dp 数组
class Solution {
public:
bool isMatch(string s, string p) {
int m = s.size(), n = p.size();
vector<vector<bool>> dp(m + 1, vector<bool>(n + 1, false));
dp[0][0] = true;//初始化很重要
for (int i = 1; i < n + 1; ++i) {
if (p[i - 1] == '*') {
dp[0][i] = dp[0][i - 2];
}
}
for (int i = 1; i < m + 1; ++i) {
for (int j = 1; j < n + 1; ++j) {
if (p[j - 1] == '.') {
dp[i][j] = dp[i - 1][j - 1];
}
else if (p[j - 1] != '*') {
dp[i][j] = dp[i - 1][j - 1] && p[j - 1] == s[i - 1];
}
else if (p[j - 2] != s[i - 1] && p[j - 2] != '.') {
dp[i][j] = dp[i][j - 2];
}
else {
dp[i][j] = dp[i-1][j - 2] || dp[i - 1][j] || dp[i][j - 2];
}
}
}
return dp[m][n];
}
};
























 588
588











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








