一些决策树的简单笔记:
2015.09.18
看了一下决策树模型,ID3的算法是自顶向下的,选择最适合作为根节点的属性。分类能力最好的属性被选为根节点的属性,采用熵表示。
1.对于布尔型分类的熵(可以看做进行编码分类所需的最小二进制位):
P+是正向样本的比例,P-是反向样本的比例。
2.对于c个状态的分类的熵定义:
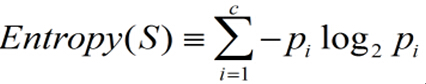
2015.09.22
一.
主要学习了用信息增益度量期望的熵降低,意思就是用信息增益的注册来使期望的熵降低的方法。
信息增益被定义为:

关于它的计算方式,跟上面的有关。
二.
注意理解ID3算法的优劣点:
1.搜索了整个空间,避免了假设空间可能不包含目标函数。
2.它这个是根据单一属性进行选择搜索的,失去了表示所有一致假设所带来的优势。
3.它是一种类似贪心式的搜索,每次选取信息增益最大的属性,容易陷入局部最优。
三.
近似的ID3算法归纳偏置:较短的树比较长的树优先。
得到的搜索树跟它的搜索策略有关。
奥坎姆剃刀:优先选择拟合数据的最简单的假设。
2015.10.07
一.过拟合数据
定义:给定一个假设空间H,一个假设h∈H,如果存在其他的假设h'∈H,使得在训练样例上h的错误率小于h',但是在整个实例分布上h'的错误率比h小,那么就说假设h过度拟合训练数据。
避免过拟合的方式:
1.及早停止树的增长,在ID3算法完美分类训练数据之前就停止树的增长。(不宜使用,无法正确的估计何时停止树增长)
2.后修剪法。允许树过度拟合数据,然后对树进行修剪。
确定树的规模的准则:
训练和验证集是两个独立的集合,一般都是2/3的训练集,1/3的验证集合。
1.错误率降低的修剪。
如果删除该节点为根的子树,采用该节点的包括样例的最常见分类作为它的值,使得此时决策树对于验证集合的性能不必原来的树差,然后就删除该节点的树。
2.规则后修剪。
⑴得到决策树,允许过拟合数据。
⑵将决策树转化为等价的规则集合,就是IF-THEN的形式。
⑶通过删除能导致估计精度提高的"前件"来修剪(泛化)规则。
⑷按照修剪过的规则的估计精度对它们进行排序。
二.合并连续值的属性
三.属性选择的其他度量标准
信息增益度量存在一个内在偏置,它偏袒具有较多值的属性。(举例,把Date作为分类的属性,那么这颗决策树会非常宽,对于训练数据有很好的效果,但是不是一个好的预测器)
分裂信息阻碍选择值为均匀分布的属性,它的计算方式如下:
其中,S1到Sc是c个值的属性A分割S而形成的c个样例子集。
此时的决策树的属性决定采用增益比率度量,它的计算方式如下:
有一个问题就是当Si接近于S时,造成分裂信息的值过小,得不到好的结果,可以采取的一种策略就是先计算每个属性的增益,挑选一些超过平均值的属性,来采用增益比率。
四.处理缺少属性值的训练样例
⑴赋给它最常见的属性值。
⑵根据概率赋值。
五.处理不同代价的属性
从社会成本和常识上来考虑,有两种相对较为常见的处理方式。









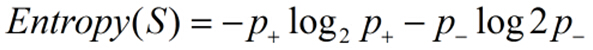
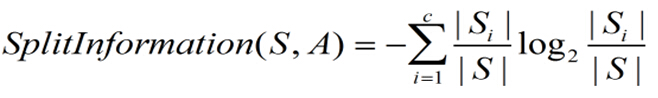
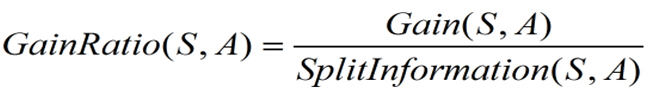














 108
108

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








