时间复杂度（原文为在下小吉.此篇仅为自己记录）

一个算法的执行时间大致上等于其所有语句执行时间的总和。

一个语句的执行时间为该条语句的重复执行次数和执行一次所需时间的乘积。

时间复杂度分类

通常用O符号表示算法的时间复杂度，大致分为以下几类：

1.常数时间复杂度：无论问题规模如何变化，算法的运行时间都保持不变。

2.线性、对数、平方、立方、指数等时间复杂度。

方法

平方阶

1 x=0;y=0;
2 for(int i=1;i<=n;i++)
3    x++;
4 for(int j=1;j<=n;j++)
5    for(int k=1;k<=n;k++)
6        y++;

该程序段里面频度最大的语句是第6句，为

立方阶

1 x=1;
2 for(int i=1;i<=n;i++)
3    for(int j=1;j<=i;j++)
4        for(int k=1;k<=j;k++)
5            x++;

该程序段里面频度最大的语句是第5句，为

对数阶

1 for(int i=1;i<=n;i*=2)
2    x++;

例子

常数复杂度O（1）

常数时间复杂度的算法执行时间与具体输入的数据规模无关，通常是表格查找、数组索引或者直接返回常量等操作。（要注意的是，链表查找并非常数复杂度算法）

线性时间复杂度O（n）

线性时间复杂度 O(n) 的算法指的是随着输入规模n的增长，该算法的运行时间呈现出线性增长趋势。也就是说，当输入规模n增加1倍时，算法的运行时间也增加了1倍。通常情况下，O(n)的算法需要对数据进行从头到尾的遍历处理。

对数时间复杂度O（logn）

对数时间复杂度 O(log n) 的算法指的是随着输入规模n的增长，该算法执行时间呈现出对数增长趋势。例如，当输入规模n增加1倍时，算法的运行时间可能会增加约2倍。常见的O(log n)算法通常是使用二分查找或者树结构等数据结构实现的。

平方时间复杂度O（）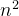

立方时间复杂度O（）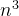

在实际编程中，由于立方阶算法的效率非常低下，通常应该尽可能避免使用它，或者通过一些技巧将其转化为更高效的算法，以提高程序的性能。

指数时间复杂度O（）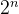

指数时间复杂度是指算法执行的时间与数据规模 n 的指数成正比，通常表示为 O(2^n)。一种计算方式是，在算法中使用了嵌套循环或递归，每次运算次数都是上一次的两倍或更多，这种情况就容易出现指数级别的时间复杂度。

易错分析

1.时间复杂度并不只能用n表示。

2.递归调用会增加程序的时间复杂度。

3.数据规模较小时，算法时间复杂度可能看起来并不显著，但随着数据规模增大，其算法时间复杂度也会明显增加。