三种基本排序

1、排序的基本概念与分类

1.1 排序的稳定性

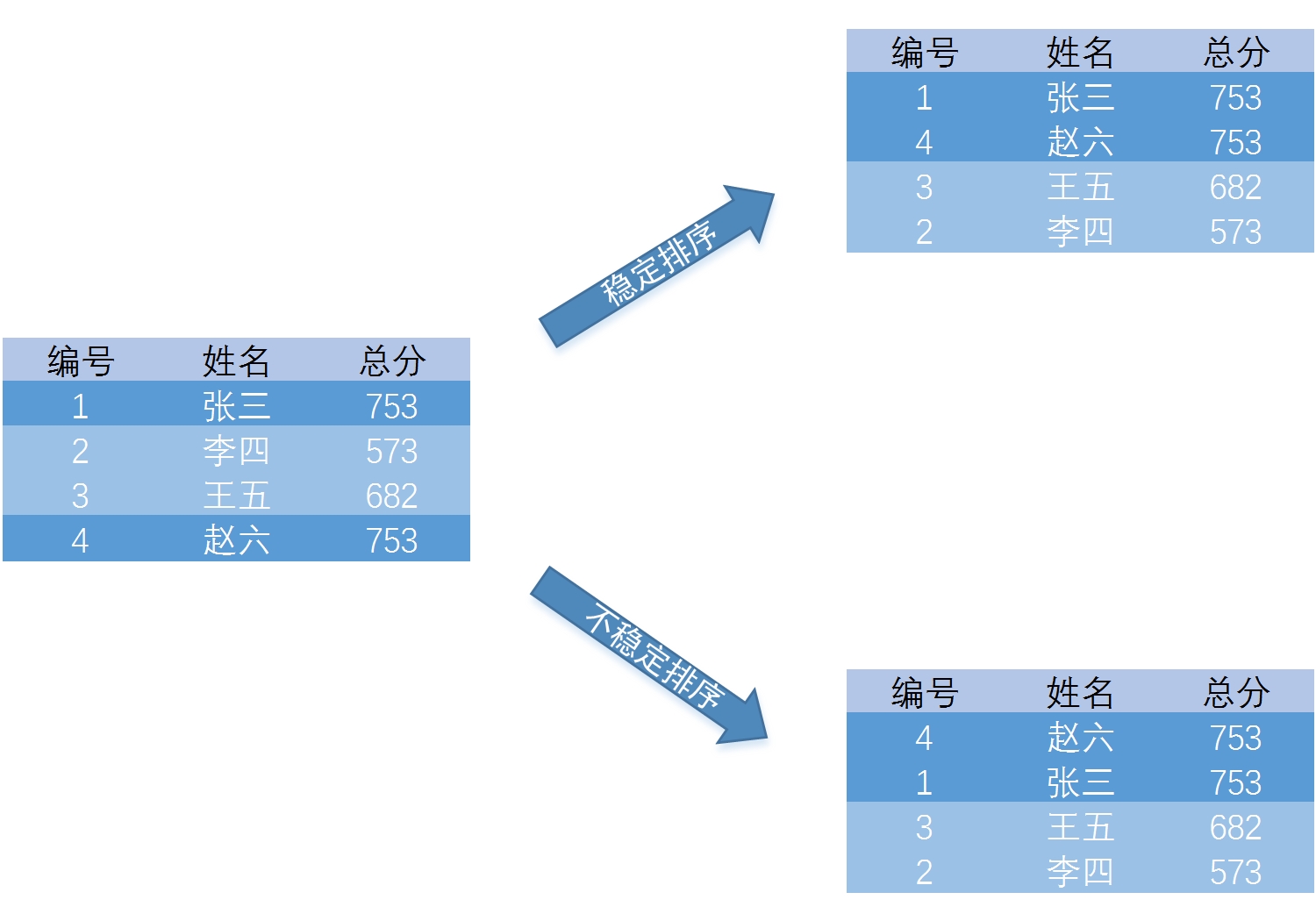
由于排序不仅是针对主关键字，那么对于次关键字，因为待排序的记录序列中可能存在两个或者两个以上的关键字相等的记录，排序结果可能会存在不唯一的情况，所以我们给出了稳定与不稳定排序的定义。

假设Ki = Kj（1<=i<=n, 1<=j<=n, i != j），且在排序前的序列中 Ri 领先于 Rj （即i < j）。如果在排序后仍然领先，则称所用的排序方法是稳定的；反之，若可能使得排序后的序列中 Rj 领先于 Ri，则称使用的排序方法是不稳定的。

1.2 内排序与外排序

根据在排序过程中待排序的记录是否全部被放置在内存中，排序分为：内排序和外排序。

内排序是在排序整个过程中，待排序的所有记录全部被放置在内存中。外排序是由于排序的记录个数太多，不能同时放置在内存，整个排序过程需要在内外存之间多次交换数据才能进行。我们这里主要介绍内排序的多种方法：

对于内排序来说，排序算法的性能主要是受3个方面的影响：

1、时间性能
在内排序中，主要进行两种操作：比较和移动。比较指关键字之间的比较，这是要做排序最起码的操作。移动指记录从一个位置移动到另一个位置，事实上，移动可以通过改变记录的储存方式来予以避免。总之，高效率的内排序算法应该具有尽可能少的关键字比较次数和尽可能少的记录移动次数。

2、辅助空间
评价排序算法的另一个主要标准是执行算法所需要的辅助储存空间。辅助储存空间是除了存放待排序所占用的储存空间之外，执行算法所需要的其他储存空间。

3、算法的复杂性
这里指的是算法本身的复杂度，而不是指算法的时间复杂度。显然算法过于复杂也会影响排序的性能。

1.3 排序要用到的结构和函数

为了方便后面的讲解，我们先提供一个用于排序的顺序表结构，此结构也将用于之后我们要讲的所有排序算法。

#define MAXSIZE 10   //可自行更改大小

typedef struct {
    int arr[MAXSIZE + 1];
    int length;
}SqList;

另外最常用的就是交换了，我们也写成一个函数，方便使用

void swap(SqList *L, int i, int j){
    int temp = L->arr[i];
    L->arr[i] = L->arr[j];
    L->arr[j] = temp;
}

接下来开始第一种排序

2、冒泡排序

2.1 最简单排序实现

冒泡排序的基本思想是：两两比较相邻记录的关键字，如果反序则交换，直到没有反序的记录为止。冒泡细分下来可以分为3种，先来看最简单的一段。

void BubbleSort0(SqList *L){
    int i, j;
    for (i = 0; i < L->length; i++)
        for (j = i + 1; j < L->length; j++)
            if (L->arr[i] > L->arr[j])
                swap(L, i, j);
}

严格来说，不算是标准的冒泡排序，因为它不满足“两两比较相邻记录”的思想，应该算是交换排序。思路就是和让每一个关键字和后面的比较，如果大就交换。这个应该算是最容易写出来的排序代码了，但是它却有缺陷。
例如 { 9，1，5，8，3，7，4，6，2 } 在排序好1，2的位置后，对其余的关键字的排序没什么帮助，3反而还被换到了最后，也就是说，这个算法的效率是非常低的。想知道具体交换次序的可以在排序函数里面用打印函数看看每一次交换后数组中是怎么回事。

2.2 冒泡排序算法

我们来看看真正的冒泡排序到底有何改进

void BubbleSort1(SqList *L){
    int i, j;
    for (i = 0; i < L->length; i++)
        for (j = L->length - 2; j >= i; j--)    //注意 j 是从后往前循环
            if (L->arr[j] > L->arr[j+1])        //若前者大于后者
                swap(L, j, j + 1);
}

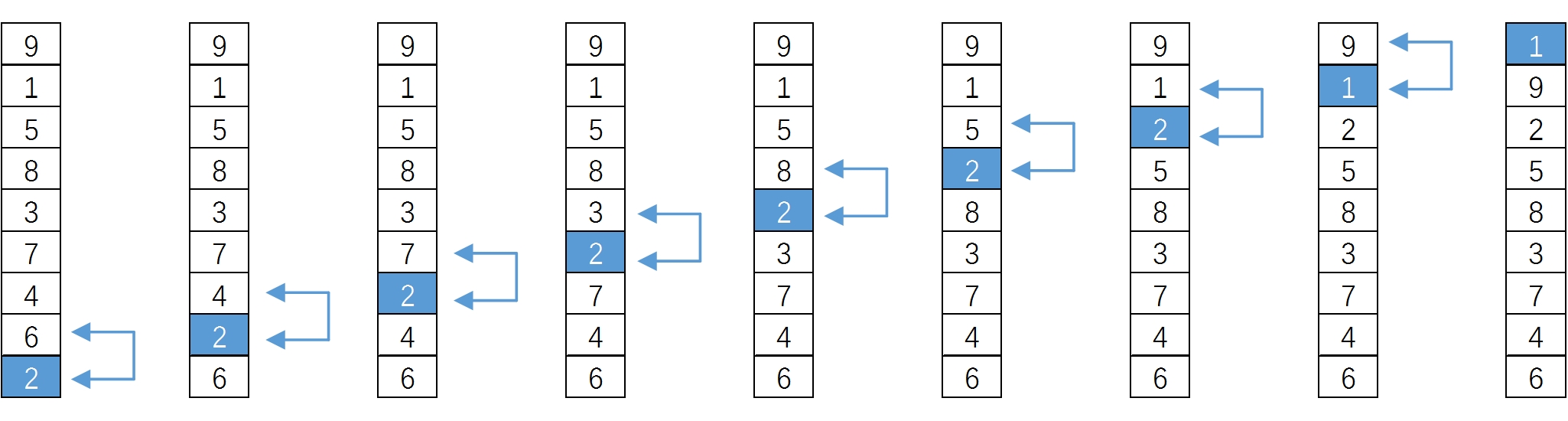
因为从后往前交换，所以，当 i = 0时，1就到了最上面，2也到了第三个位置。往后的话，数据交换更简单，在越多的数据排序中，这种优势就更能体现出来，较小的数字如同气泡一样慢慢浮到上面，因此就将该算法命名为冒泡算法。此处，只提供第一次排序的示意图，全部过程就自己和上面一样，用输出函数自己打印观察了。

2.3 冒泡排序优化

当然这样的冒泡排序是还可以优化的。如果我们的待排序序列式 {2，1，3，4，5，6，7，8，9} ，也就是说，除了1和2意外的，都已经是正常的顺序了，那么，当 i = 1时，交换了2和1，此时序列已有序，但是算法依旧会将从 i = 2到9所有的都执行了一遍，尽管没有交换，但是大量的比较还是多于的。为了改变这个现状，我们使用一个flag来改进：

void BubbleSort2(SqList *L){
    int i, j;
    bool flag = true;     //flag作为标记
    for (i = 0; i < L->length && flag; i++){       //若flag为true则退出循环
        flag = false;                             //初始化为flase
        for (j = L->length - 2; j >= i; j--){    
            if (L->arr[j] > L->arr[j+1]){        
                swap(L, j, j + 1);
                flag = true;      //如果有交换，则flag为true
            }
        }
    }
}

代码改动的关键就在于 i 变量的循环中增加了flag，可以避免一些无意义的循环，在性能上就有一些提升。

2.4 冒泡排序复杂度分析

当最好的情况下，如果本来就是有序的，那么根据改进后的代码，就有 n-1 次的比较，没有交换，时间复杂度为 O[n]，当最坏的情况，即待排序的表是逆序的情况，此时需要比较 n(n-1)/2 次，并作等数量级的记录移动，因此总的时间复杂度是O[n^2]。

3、简单选择排序

3.1 简单选择排序算法

简单选择排序法就是通过 n - i 次关键字间的比较，从 n - i + 1个记录中选出关键字最小的记录 ，并和第 i (1<=i<=n) 个记录交换，我们来看代码：

void InsertSort(SqList *L){
    int i, j, min;
    for (i = 0; i < L->length; i++){
        min = i;             //将当前下标定义为最小下标
        for (j = i + 1; j < L->length; j++){
            if (L->arr[min] > L->arr[j])   //如果有小于当前最小值的关键字
                min = j;      //将此关键字的下标赋值给min
        }
        if (i != min)
            swap(L, i, min);
    }
}

这段代码不难理解，我们也以 {9，1，5，8，3，7，4，6，2} 为例，对 i 从1循环到8.当 i = 1时，L->arr[i] = 9，min开始是1，然后与 j = 2到9比较大小，因为 j = 2时最小，所以min = 2。最终交换了L->arr[1]与L->arr[0]的值，如图所示，注意，比较8次，却只交换数据操作一次。

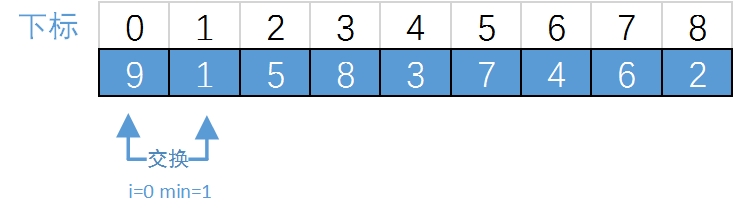
后面的也是一个道理，如果想看每一次的处理结果，可以在循环里面加输出函数，就不多说了，这组排序只需要8次就可以完成。

3.2 简单选择排序复杂度分析

从简单选择排序的过程来看，它最大的特点就是交换移动数据次数相当地少，也就节约了时间。分析它的时间复杂度分析可以发现，无论是最好还是最坏的情况，需要比较的次数都是一样多的，第 i 趟排序需要进行 n - i 次关键字的比较，此时需要比较 n(n-1)/2 次。而对于交换次数来说，最好的时候只需要0次，最差的时候，需要 n-1 次，最好的排序时间应该是比较和交换的总和，因此，总的时间复杂度也是 O[n^2] ，虽然说复杂度和冒泡排序是一样的，但是性能上还是要略优于冒泡排序的。

4、直接插入排序

4.1 直接插入排序算法

直接插入排序的基本操作是将一个记录插入到已经排好序的有序表中，从而得到一个新的、记录数+1的有序表。下面我们直接来看代码。

void InsertSort(SqList *L){
    int i, j, temp;
    for (i = 1; i < L->length; i++){
        if (L->arr[i] < L->arr[i - 1]){    //需要将L->arr[i]插入
            temp = L->arr[i];         //设置标志，用temp存储
            for (j = i - 1; L->arr[j] > temp; j--)
                L->arr[j + 1] = L->arr[j];      //记录后移
            L->arr[j + 1] = temp;    //插入到正确位置
        }
    }
}

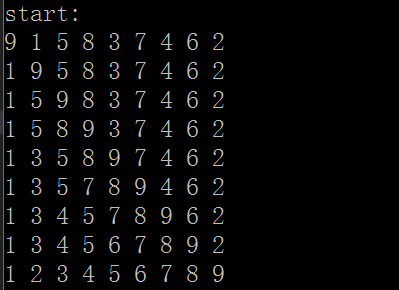
从这个每次插入排序后的序列顺序，我们可以看到，从 i = 1开始比较，使用temp记录 arr[i] 的数据，然后一个for循环遍历 i 之前的数据，找到合适位置，在遍历的同时，将不满足条件的位置上的数依次后移，最后，将temp（也就是arr[i]）放在该插入的位置。这就是直接插入排序的基本思路。

4.2 直接插入排序复杂度分析

从空间上来看，只需要一个记录的辅助空间，所以可以忽略，关键是看时间复杂度。

1、当最好的情况，也就是要排序的表本身就是有序的，那么比较次数就是 n-1 次，而且每次都是L->arr[i] > L->arr[i-1]，所以也就没有移动记录（不需要temp），即时间复杂度为 O[n] 。

2、当最坏的情况，也就是本身是逆序的，那么此时的比较次数就是 (n+2)(n-1)/2 次，记录的次数也达到了最大值 (n+4)(n-1)/2 次。

3、当排序是随机的情况，那么概率是平均的，也就是说平均比较和移动的次数约为 （n^2）/4 次，因此，我们得出直接插入排序的时间复杂度为 O[n^2] 。当然我们也可以看出，同样是 O[n^2] 的时间复杂度，但是直接插入排序的性能比前面两个都要好。

以上就是三种基本排序，后续的学习中还会继续补充其他的排序方法。