题目连接:
http://acm.tzc.edu.cn/acmhome/problemdetail.do?&method=showdetail&id=1005
题目分类:
搜索 - 最优路径
数据结构:
struct NODE{
int x,y //坐标
int H; //启发式估计 值等于与终点横纵坐标差的和
int STEP; //步数
}
deque _OPEN,_CLOSE //开表,关表队列
NODE [][] //地图思路分析:
--------------------------------------------------------------------------------------------
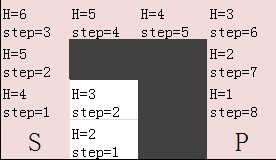
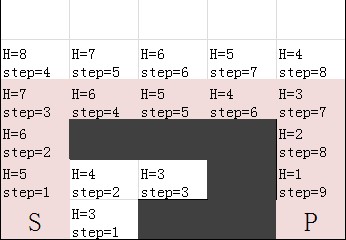
A* 算法:
用于求得最短寻路问题
从起点开始,每一步都需要依靠启发式函数来估计接下去需要走的路.
这样可以最大限度的跳过没有必要的路.
相对于广度搜索,它的效率十分的高.几乎所有的路线都是贴最近的路走.
将起点列入 开启列表中,它表明了那些点曾经被访问过.也就是那些待考证的点.
因为列表中暂时唯一只有起点,所以将它拿出来,列入 关闭列表 ,代表已经访问过,不必在访问.
围绕刚拿出来的点,考察它周围所有的点,记录下H值和从该点到周围点的步数(+1).
并一一放入 开启列表 里.
将开启列表按照H值从小到大排序,因为我们暂且需要更有希望近的点.虽然还未真正的知道.
讲H值最小(也就是最近)的点同刚开始的起点一样,从 开启列表 中取出,放入关闭列表.
重复上述步骤.
一旦发现刚才的选择是一条死路,也不要紧.
因为前面的途中都讲有可能的点(尽管希望没有选择的那条路大)都保存在开启列表里.
只需从开启列表中,选择最近 第二有希望的点继续拓展.
因为之前记录过步数(代表从拓展点走到另一个点的步数),所以不会发现绕路的现象.
每个点都是由之前的点 "直径" 走来,相当于它的父节点
这样就可以略去 死路走过的节点.
如此下去,直到找到终点
或者开启列表中已经没有任何节点,代表不可能由起点走向终点.
所以,实际上"死路"那部分的路径是探测过的,而且实实在在跟正确路径一样保存在关闭列表里.
只是题目只求最短步数,不求实际路径.则可以借由记录STEP步数来忽略那部分走的路.
证明:
简略的说,
从起点开始假设能搜到N个周围的点(上下左右),
代表有N条可能的希望.并保存在开启列表中
假设
沿着某一条最有希望的点,
该点最后没有任何可以搜索的点,则表明该点周围已经没有路
则可以选择当初在开启列表中第二有希望的点继续探查.
相当于有足够数量的人走迷宫
每个人拿着计步器
当看见分叉时,由一个人带着计步器选择最有希望的路
另外个人在原地等待.
一旦发现那条路行不通,则有第二个人继续走第二有希望的路线.
以此类推.
假设有那么一条路径通向终点,
则必定是最优路线.
因为比它有希望的路线或已被证明是死路
假设所有的路都是死路,
则可以证明在起点的时候选择都是 未来没有希望的路.
所以可以证明,必能选择一条正确的路
要么是最优路线,要么可以得出所有的路都不行
源代码:
#include <iostream>
#include <stdio.h>
#include <queue>
using namespace std;
struct NODE
{
char C;
int x,y;
int H; // 曼哈顿估算 因为只能上下左右,所以G(步长)值无意义
int step;
bool operator < (const NODE & k) const{ //重载比较运算符
return H < k.H;
}
bool operator == (const NODE & k) const{
return x == k.x && y == k.y;
}
};
/* 寻找节点 n 是否存在于队列 ns 中 */
deque<NODE>::iterator isfinded(NODE n,deque<NODE> &ns)
{
deque<NODE>::iterator nsp=ns.begin();
while(nsp!=ns.end())
{
if(*nsp==n) return nsp;
nsp++;
}
return ns.end();
}
int AStar(NODE map[21][21],NODE start,NODE end,int n,int m)
{
NODE CNODE;
deque<NODE> _OPEN,_CLOSE;
deque<NODE>::iterator _TMPO,_TMPC;
start.step=0; //记起点节点步数为0
_OPEN.push_back(start);
while(_OPEN.size()!=0)
{
sort(_OPEN.begin(),_OPEN.end()); //按H值进行升序排序
CNODE=_OPEN.front();
_OPEN.pop_front();
_CLOSE.push_back(CNODE);
if(CNODE==end)
{
return CNODE.step; //返回总步数
}
else
{
for(int i=-1;i<=1;i++)
for(int j=-1;j<=1;j++)
// 判断i,j其一为0且不都为0 (只能选上下左右,且不能选自身格子) 另外周围的格子不能越界
if( (i==0 || j==0 ) && ( i!=0 || j!=0 ) && CNODE.x+i<n && CNODE.y+j<m && CNODE.x+i>=0 && CNODE.y+j>=0)
{
NODE newNode=map[CNODE.x+i][CNODE.y+j],tmp; //建立新临时节点
_TMPO=isfinded(newNode,_OPEN); //是否在OPEN表中
_TMPC=isfinded(newNode,_CLOSE); //是否在CLOSE表中
if(_TMPO==_OPEN.end() && _TMPC==_CLOSE.end())//新节点同时不在两张表中
if(newNode.C!='*') //且不为障碍物
{
newNode.H= ( abs( end.x-newNode.x )+abs( end.y-newNode.y) )*10;
newNode.step=CNODE.step+1; //记下步数
_OPEN.push_front(newNode);
}
}
}
}
return 0;
}
int main()
{
int i,j,N,M,T,path;
NODE tower[21][21],start,end;
while(scanf("%d%d%d",&N,&M,&T) && ( N || M || T))
{
for(i=0;i<N;i++)
{
getchar();
for(j=0;j<M;j++)
{
scanf("%c",&tower[i][j].C);
tower[i][j].x=i; tower[i][j].y=j;
if(tower[i][j].C=='S')
start=tower[i][j];
if(tower[i][j].C=='P')
end=tower[i][j];
}
}
path=AStar(tower,start,end,N,M);
if(path<=T && path>0)
printf("YES\n");
else
printf("NO\n");
}
return 0;
}























 6513
6513

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








