2025 CSP-S 提高组题目解析

2025 CSP-S 提高组题目解析

一、单项选择题（每题2分，共30分）

1. 红蓝球不相邻排列

题目：有5个红色球和5个蓝色球，除颜色外完全相同。将10个球排成一排，要求任意两个蓝色球都不能相邻，有多少种不同的排列方法？
选项：A.25 B.30 C.6 D.120
答案：C
解析：采用「插空法」解决不相邻排列问题，步骤如下：

1. 先排无限制元素：5个红色球完全相同，排成一排后产生 5+1=6 个间隙（含两端，如 _ R _ R _ R _ R _ R _），红球排列仅1种。
2. 选间隙放限制元素：5个蓝色球完全相同，需从6个间隙中选5个放置（避免相邻），组合数为 C(6,5)=6（组合数公式 C(n,k)=n!/(k!(n-k)!)，此处 C(6,5)=6）。
3. 总排列数：红球与蓝球排列均无顺序差异，最终结果为6。

2. KMP算法next数组

题目：在KMP算法中，对于模式P=“abacaba”，其next数组（next[i]定义为模式P[0…i]的最长公共前后缀长度，且长度≠子串长度，数组下标从0开始）的值是什么？
A.[0,0,1,0,1,2,3]
B.[0,1,2,3,4,5,6]
C.[0,0,1,1,2,2,3]
D.[0,0,0,0,1,2,3]
答案：A
解析：next数组核心是「找前缀与后缀的最长公共长度（排除自身）」，计算过程如下表：

模式串下标	子串P[0…i]	前缀（不含最后一个字符）	后缀（不含第一个字符）	最长公共长度	next[i]
0	“a”	无	无	0	0
1	“ab”	[“a”]	[“b”]	0	0
2	“aba”	[“a”,“ab”]	[“a”,“ba”]	1（“a”）	1
3	“abac”	[“a”,“ab”,“aba”]	[“c”,“ac”,“bac”]	0	0
4	“abaca”	[“a”,“ab”,“aba”,“abac”]	[“a”,“ca”,“aca”,“baca”]	1（“a”）	1
5	“abacab”	[“a”,“ab”,“aba”,“abac”,“abaca”]	[“b”,“ab”,“cab”,“acab”,“bacab”]	2（“ab”）	2
6	“abacaba”	前6个字符的所有前缀	后6个字符的所有后缀	3（“aba”）	3

最终next数组为 [0,0,1,0,1,2,3]。

3. 满线段树区间查询节点数

题目：对一个大小为16（下标0-15）的数组构建满线段树。查询区间[3,11]时，最少需要访问多少个树结点（包括路径上的父结点和完全包含在查询区间内的结点）？
A.7
B.8
C.9
D.10
答案：B
解析：

1. 满线段树结构：大小16的数组对应满二叉树，叶子节点16个（对应数组元素0-15），内部节点15个，总节点31个。树的层次为4（根为第1层，叶子为第4层）。
2. 区间分解逻辑：查询区间[3,11]需分解为线段树中「完全包含的节点」，分解结果为：
   • 叶子节点：[3,3]
   • 内部节点：[4,7]（覆盖4-7）、[8,11]（覆盖8-11）
3. 路径节点计数：从根到分解节点的路径需访问的父节点包括：根（[0-15]）、左子树（[0-7]）、右子树（[8-15]）、[0-3]、[2-3]，加上分解后的3个节点，共8个节点。

4. Trie树节点数统计

题目：将字符串"cat",“car”,“cart”,“case”,“dog”,"do"插入一个空的Trie树（前缀树）中。构建完成的Trie树（包括根节点）共有多少个结点？
A.8
B.9
C.10
D.11
答案：D
解析：Trie树每个节点代表一个字符，插入过程（含根节点）如下：

1. 根节点：初始空Trie树有1个根节点。
2. 插入"cat"：根→c→a→t，新增3个节点（累计4）。
3. 插入"car"：根→c→a→r，新增1个节点（a的子节点r，累计5）。
4. 插入"cart"：根→c→a→r→t，新增1个节点（r的子节点t，累计6）。
5. 插入"case"：根→c→a→s→e，新增2个节点（a的子节点s、s的子节点e，累计8）。
6. 插入"dog"：根→d→o→g，新增3个节点（d、o、g，累计11）。
7. 插入"do"：根→d→o，已存在（d和o均已创建），无新增。
   总节点数为11。

5. DAG拓扑排序数量

题目：对于一个包含n个结点和m条边的有向无环图（DAG），其拓扑排序的结果有多少种可能？
A.只有1种
B.最多n种
C.等于n-m种
D.以上都不对
答案：D
解析：DAG的拓扑排序数量无固定规律，需结合具体结构判断：

• 例1：链状DAG（如 1→2→3），仅1种拓扑排序（1→2→3）；
• 例2：无向边DAG（如3个孤立节点），拓扑排序有 3!=6 种；
• 例3：含分支DAG（如 1→2,1→3），拓扑排序有2种（1→2→3、1→3→2）。
  选项A（仅1种）、B（最多n种）、C（n-m种）均不成立，故选择D。

6. 哈希表线性探查

题目：在一个大小为13的哈希表中，使用闭散列法的线性探查来解决冲突。哈希函数为H(key)=key mod 13。依次插入关键字18,26,35,9,68,74。插入74后，它最终被放置在哪个索引位置？
A.5
B.7
C.9
D.11
答案：D
解析：线性探查规则：冲突时索引+1，直到找到空位置，插入过程如下：

1. 18 mod13=5：位置5为空，插入（位置5：18）。
2. 26 mod13=0：位置0为空，插入（位置0：26）。
3. 35 mod13=9：位置9为空，插入（位置9：35）。
4. 9 mod13=9：位置9冲突，探查10（空），插入（位置10：9）。
5. 68 mod13=3：位置3为空，插入（位置3：68）。
6. 74 mod13=9：位置9冲突→10冲突→11空，插入（位置11：74）。
   最终74放在位置11。

7. 完全图最小生成树

题目：一个包含8个顶点的完全图（顶点编号1-8），任意两点之间的边权重等于两顶点编号的差的绝对值（如顶点3和7之间的边权重为|7-3|=4）。该图的最小生成树总权重是多少？
A.7
B.8
C.9
D.10
答案：A
解析：最小生成树（MST）需连接所有顶点且总权重最小，规则如下：

1. 完全图中最小边权重为1（相邻编号顶点的边，如1-2、2-3等）。
2. 8个顶点的MST需7条边（n个顶点的MST有n-1条边），选择7条权重为1的相邻边（如1-2、2-3、3-4、4-5、5-6、6-7、7-8）。
3. 总权重：1×7=7。

8. 二叉搜索树（BST）遍历

题目：如果一棵二叉搜索树的后序遍历序列是2,5,4,8,12,10,6，那么该树的前序遍历是什么？
A.6,4,2,5,10,8,12
B.6,4,5,2,10,12,8
C.2,4,5,6,8,10,12
D.12,8,10,5,2,4,6
答案：A
解析：BST特性：左子树所有节点值<根节点值<右子树所有节点值；后序遍历为「左→右→根」，步骤如下：

1. 找根节点：后序序列最后一个元素6为根。
2. 分左右子树：
   • 左子树：序列中<6的元素「2,5,4」（根为4，左子树2，右子树5）；
   • 右子树：序列中>6的元素「8,12,10」（根为10，左子树8，右子树12）。
3. 构建BST结构：

       6
     /   \
    4     10
   / \   /  \
   

2 5 8 12

4. **前序遍历**：根→左→右，即 `6→4→2→5→10→8→12`。


### 9. 0-1背包最大价值
**题目**：一个0-1背包问题，背包容量为20。现有5个物品，其重量和价值分别为（7,15）、（5,12）、（4,9）、（3,7）、（6,13）。装入背包的物品能获得的最大总价值是多少？  
A.43 
B.41 
C.45 
D.44  
**答案**：D  
**解析**：0-1背包需在容量限制内选择物品使价值最大，枚举最优组合：  
- 组合1：重量7（15）+4（9）+3（7）+6（13）=20，价值15+9+7+13=44；  
- 组合2：重量7（15）+5（12）+4（9）=16（剩余4，无合适物品），价值15+12+9=36；  
- 组合3：重量5（12）+4（9）+3（7）+6（13）=18（剩余2），价值12+9+7+13=41；  
最大价值为44。


### 10. 最近公共祖先（LCA）
**题目**：在一棵以结点1为根的树中，结点12和结点18的最近公共祖先（LCA）是结点4。那么下列哪个结点的LCA组合是不可能出现的？  
A.LCA(12,4)=4 
B.LCA(18,4)=4 
C.LCA(12,18,4)=4 
D.LCA(12,1)=4  
**答案**：D  
**解析**：LCA定义：两个节点的最深公共祖先，结合「根为1，LCA(12,18)=4」的条件：  
- A：4是12的祖先（12→...→4），故LCA(12,4)=4，可能；  
- B：4是18的祖先（18→...→4），故LCA(18,4)=4，可能；  
- C：12、18、4的公共祖先为4，故LCA=4，可能；  
- D：1是根，12的祖先包括4和1，故LCA(12,1)=1（根），而非4，不可能。


### 11. 分治算法时间复杂度
**题目**：递归关系式 \(T(n)=2T(n/2)+O(n^2)\) 描述了某个分治算法的时间复杂度。请问该算法的时间复杂度是多少？  
A.O(n) 
B.O(n log n) 
C.O(n²) 
D.O(n² log n)  
**答案**：C  
**解析**：用「主定理」分析（主定理：\(T(n)=aT(n/b)+f(n)\)）：  
1. 对应参数：\(a=2\)（子问题数量），\(b=2\)（子问题规模），\(f(n)=O(n²)\)（合并时间）。  
2. 计算临界指数：\(log_b a = log_2 2 = 1\)。  
3. 比较合并时间与子问题时间：\(f(n)=n² = Ω(n^{1+ε})\)（ε>0，如ε=1），满足主定理「Case 3」（合并时间主导）。  
4. 结论：\(T(n)=O(f(n))=O(n²)\)。


### 12. 最小堆操作
**题目**：在一个初始为空的最小堆（min-heap）中，依次插入元素20,12,15,8,10,5。然后连续执行两次“删除最小值”（delete min）操作。请问此时堆顶元素是什么？  
A.10 
B.12 
C.15 
D.20  
**答案**：A  
**解析**：最小堆特性：父节点值≤子节点值，插入与删除步骤如下：  
1. **插入后堆结构**（数组表示）：`[5,8,10,20,12,15]`（堆顶为5）。  
2. **第一次删除最小值（5）**：  
- 用最后元素15替换根，调整堆：15与左子树8交换→15与右子树12交换，最终堆为 `[8,12,10,20,15]`（堆顶8）。  
3. **第二次删除最小值（8）**：  
- 用最后元素15替换根，调整堆：15与左子树12交换→15与右子树10交换（不满足最小堆，需再调整），最终堆为 `[10,12,15,20]`（堆顶10）。  
此时堆顶元素为10。


### 13. 容斥原理计数
**题目**：1到1000之间，不能被2、3、5中任意一个数整除的整数有多少个？  
A.266
B.267 
C.333 
D.734  
**答案**：A  
**解析**：用「容斥原理」计算“能被至少一个数整除”的数，再用总数减去该值：  
1. 定义集合：  
- A：能被2整除的数，\(|A|=⌊1000/2⌋=500\)；  
- B：能被3整除的数，\(|B|=⌊1000/3⌋=333\)；  
- C：能被5整除的数，\(|C|=⌊1000/5⌋=200\)。  
2. 交集计算：  
- \(|A∩B|=⌊1000/6⌋=166\)（能被6整除）；  
- \(|A∩C|=⌊1000/10⌋=100\)（能被10整除）；  
- \(|B∩C|=⌊1000/15⌋=66\)（能被15整除）；  
- \(|A∩B∩C|=⌊1000/30⌋=33\)（能被30整除）。  
3. 容斥公式：  
\(|A∪B∪C|=|A|+|B|+|C|-|A∩B|-|A∩C|-|B∩C|+|A∩B∩C|=500+333+200-166-100-66+33=734\)。  
4. 不能被整除的数：\(1000-734=266\)。


### 14. 斐波那契递归与动态规划差异
**题目**：斐波那契数列的定义为F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)。使用朴素递归方法计算F(n)的时间复杂度是指数级的，而使用动态规划（或迭代）方法的时间复杂度是线性的。造成这种巨大差异的根本原因是？  
A.递归函数调用栈开销过大 
B.操作系统对递归深度有限制 
C.朴素递归中存在大量的重叠子问题未被重复利用 
D.动态规划使用了更少的数据存储空间  
**答案**：C  
**解析**：  
- 朴素递归（如 `F(5)=F(4)+F(3)`）存在大量**重叠子问题**：计算F(5)需F(4)和F(3)，计算F(4)又需F(3)和F(2)，F(3)被重复计算多次，导致时间复杂度为O(2ⁿ)（指数级）。  
- 动态规划通过「存储子问题结果」（如用数组dp[i]存F(i)），避免重复计算，每个子问题仅计算一次，时间复杂度降至O(n)（线性级）。  
- 选项A（栈开销）、B（递归深度）、D（存储空间）均非根本原因。


### 15. 任务调度最小惩罚
**题目**：有5个独立的、不可抢占的任务A1,A2,A3,A4,A5需要在一台机器上执行（从时间0开始），每个任务的处理时长和截止时刻分别为（3,5）、（4,10）、（2,3）、（5,15）、（1,11）。若任务超时，惩罚等于其处理时长。为了最小化总惩罚，应该优先执行哪个任务？  
A.处理时间最短的任务A5 
B.截止时间最早的任务A3 
C.处理时间最长的任务A4 
D.任意一个任务都可以  
**答案**：B  
**解析**：任务调度最优策略为「截止时间最早（EDD）」，可最小化超时惩罚，分析如下：  
1. 任务信息整理：  
| 任务 | 处理时长 | 截止时刻 |
|------|----------|----------|
| A1   | 3        | 5        |
| A2   | 4        | 10       |
| A3   | 2        | 3        |
| A4   | 5        | 15       |
| A5   | 1        | 11       |
2. 按EDD排序执行：A3（2/3）→A1（3/5）→A2（4/10）→A5（1/11）→A4（5/15）：  
- A3：完成时间2≤3（无惩罚）；  
- A1：完成时间2+3=5≤5（无惩罚）；  
- A2：完成时间5+4=9≤10（无惩罚）；  
- A5：完成时间9+1=10≤11（无惩罚）；  
- A4：完成时间10+5=15≤15（无惩罚）；  
总惩罚为0。  
3. 其他策略对比：  
- 选A5（SPT策略）：A5→A3→A1，A1完成时间1+2+3=6>5（惩罚3）；  
- 选A4（最长时间）：A4→A3，A3完成时间5+2=7>3（惩罚2）；  
故优先选择截止时间最早的A3。


## 二、程序阅读（共40分）
### 第一题：受限全排列统计（🔶1-80至🔶1-105）
#### 完整程序（修正语法错误后）
```c
#include <algorithm>
#include <cstdio>
#include <cstring>
bool flag[27];  // 标记元素是否已使用（true=已用，false=未用）
int n;          // 输入的排列长度（1~n的全排列）
int p[27];      // 存储当前排列（p[k]表示第k位选择的元素）
int ans = 0;    // 符合条件的排列总数

// 递归生成排列：k表示当前要确定第k位元素
void dfs(int k) {
 if (k == n + 1) {  // 递归终止：已确定n位元素（生成一个有效排列）
     ans++;          // 符合条件的排列数+1
     return;
 }
 // 遍历所有可能的元素（1~n）
 for (int i = 1; i <= n; ++i) {  // 原代码“i<n”修正为“i<=n”（覆盖1~n）
     if (flag[i]) continue;      // 跳过已使用的元素（避免重复）
     // 排除“当前元素=前一个元素+1”的情况（相邻递增限制）
     if (k > 1 && i == p[k - 1] + 1) continue;  // 原代码“i--”修正为“i==”
     flag[i] = true;  // 标记元素i为已使用
     p[k] = i;        // 第k位选择元素i
     dfs(k + 1);      // 递归确定第k+1位元素
     flag[i] = false; // 回溯：标记元素i为未使用（关键！否则元素无法复用）
 }
 return;
}

int main() {
 scanf("%d", &n);  // 输入排列长度n
 dfs(1);           // 从第1位开始生成排列
 printf("%d\n", ans);  // 输出符合条件的排列数
 return 0;
}

程序功能分析

该程序生成1~n的全排列，排除“当前元素=前一个元素+1”（相邻递增） 的排列，统计符合条件的排列总数。核心逻辑：

1. 递归（DFS）：从第1位到第n位依次确定排列元素，k表示当前要确定的位置；
2. 标记与回溯：用flag数组标记元素是否已使用，递归返回后回溯（flag[i]=false），确保元素可重复用于其他排列；
3. 限制条件：k>1 && i==p[k-1]+1 排除相邻递增的情况（如排列中出现“2,3”“4,5”等）。

题目解析（6个小题）

1. （1分）当输入的n=3的时候，程序输出的答案为3

• 选项：正确/错误
• 答案：正确
• 解析：1~3的全排列共6种，符合条件的排列为：
  • 132（无相邻递增）、213（无相邻递增）、321（无相邻递增），共3种，故输出3。

2. （1分）在dfs函数运行过程中，k的取值会满足1≤k≤n+1

• 选项：正确/错误
• 答案：正确
• 解析：
  • 递归初始调用dfs(1)，k从1开始；
  • 每次递归调用dfs(k+1)，直到k=n+1时终止（递归出口）；
  • 故k的取值范围为1≤k≤n+1。

3. （1分）删除第19行的“flag[i]=false”，对答案不会产生影响

• 选项：正确/错误
• 答案：错误
• 解析：flag[i]=false是「回溯操作」，作用是重置元素的使用状态。删除后，元素被标记为true（已用）后无法重置，后续循环无法使用该元素，导致排列生成中断（如n=3时，第一次生成132后，元素1、3、2均为已用，无法生成其他排列），答案大幅减少。

4. （3分）当输入的n=4的时候，程序输出的答案为

• 选项：A.11 B.12 C.24 D.9
• 答案：D（9）
• 解析：1~4的全排列共24种，排除相邻递增的排列后，符合条件的共9种，例如：
  1324、1423、2143、2314、2413、3142、3214、3412、4132。

5. （3分）如果因为某些问题，导致程序运行第25行的dfs函数之前，数组p的初值并不全为0，则对程序的影响是

• 选项：A.输出的答案比原答案要小 B.无法确定输出的答案 C.程序可能陷入死循环 D.没有影响
• 答案：D（没有影响）
• 解析：
  • 数组p仅在递归中赋值（第18行p[k]=i），k>1时使用的p[k-1]是上一次递归的赋值结果（如k=2时，p[1]是dfs(1)中赋值的元素），与初始值无关；
  • 排列的生成依赖flag数组（标记元素是否使用），p的初始值不影响逻辑。

6. （3分）假如删去第14行的“if(flag[i])continue;”，输入3，得到的输出答案是

• 选项：A.27 B.3 C.16 D.12
• 答案：A（27）
• 解析：删去flag[i]判断后，不限制元素重复使用（即排列可包含重复元素）：
  • 第1位有3种选择（1、2、3）；
  • 第2位有3种选择（1、2、3，无使用限制）；
  • 第3位有3种选择；
    总排列数为3×3×3=27（仅排除相邻递增的情况，但重复元素的排列已大幅增加）。

第二题：鸡蛋掉落猜测

完整程序

#include <algorithm>
#include <cstdio>
#include <cstring>
#define ll long long
int cnt_broken = 0;  // 打碎的鸡蛋数量（限制最多2个）
int cnt_check = 0;   // 猜测次数（调用check函数的次数）
int n, k;            // n=总楼层，k=临界楼层（从k层扔鸡蛋碎，k-1层不碎）

// 从h层扔鸡蛋，返回是否打碎（h>=k则碎，h<k则不碎）
inline bool check(int h) {
    printf("now check:%d\n", h);
    ++cnt_check;  // 每次调用check，猜测次数+1
    if (cnt_broken == 2) {  // 已打碎2个鸡蛋，无法继续测试
        printf("You have no egg!\n");
        return false;
    }
    if (h >= k) {  // 鸡蛋打碎（h>=临界楼层k）
        ++cnt_broken;
        return true;
    } else {       // 鸡蛋未碎（h<临界楼层k）
        return false;
    }
}

// 验证h是否为临界楼层k
inline bool assert_ans(int h) {
    if (h == k) {
        printf("You are Right using %d checks\n", cnt_check);
        return true;  // 猜测正确
    } else {
        printf("Wrong answer!\n");
        return false; // 猜测错误
    }
}

// 策略1：线性查找（从1到n依次猜测，打碎即停止）
inline void guess1(int n) {
    for (int i = 1; i <= n; ++i) {
        if (check(i)) {  // 第一次打碎，i即为临界楼层k
            assert_ans(i);
            return;
        }
    }
}

// 策略2：最优查找（鸡蛋掉落问题最优策略，最小化猜测次数）
inline void guess2(int n) {
    int w = 0;
    // 找最大w，使w*(w+1)/2 <n（确定初始猜测步长，基于鸡蛋掉落问题公式）
    for (w = 1; w * (w + 1) / 2 < n; ++w);
    int ti = w;    // 当前步长（初始为w）
    int nh = w;    // 初始猜测楼层（第一步猜w层）
    while (1) {
        if (check(nh)) {  // 鸡蛋打碎：从nh-ti到nh-1线性查找
            ti--;
            for (int j = nh - ti; j < nh; ++j) {
                if (check(j)) {
                    assert_ans(j);
                    return;
                }
            }
            assert_ans(nh);
            return;
        } else {  // 鸡蛋未碎：下一个猜测楼层=当前+步长（步长-1）
            ti--;
            if (ti == 0) {  // 步长为0，剩余楼层只有n，直接猜测
                assert_ans(n);
                return;
            }
            nh = std::min(nh + ti, n);  // 避免超出总楼层n
        }
    }
}

int main() {
    scanf("%d%d", &n, &k);  // 输入总楼层n和临界楼层k
    int t;
    scanf("%d", &t);        // 输入策略类型（1=线性，2=最优）
    if (t == 1) {
        guess1(n);
    } else {
        guess2(n);
    }
    return 0;
}

程序功能分析

该程序模拟「鸡蛋掉落问题」，通过两种策略猜测临界楼层k（从k层扔鸡蛋碎，k-1层不碎），核心逻辑：

1. check函数：模拟从h层扔鸡蛋，返回是否打碎（h>=k则碎），统计猜测次数（cnt_check）和打碎鸡蛋数（cnt_broken，限制最多2个）；
2. 策略1（guess1）：线性查找，从1到n依次猜测，第一次打碎即确定k（适合鸡蛋数量充足的场景）；
3. 策略2（guess2）：最优查找，基于鸡蛋掉落问题的数学模型（步长递减），最小化猜测次数（适合鸡蛋数量有限的场景，如最多2个）。

题目解析（6个小题）

1. （1.5分）当输入为“6 5 1”时，猜测次数为5；当输入“6 5 2”时，猜测次数为3

• 选项：正确/错误
• 答案：正确
• 解析：
  • 输入“6 5 1”（n=6,k=5,t=1）：策略1线性查找，依次猜1、2、3、4、5（第5次打碎），猜测次数5；
  • 输入“6 5 2”（n=6,k=5,t=2）：策略2最优查找，步骤如下：
    1. 初始w=3（3×4/2=6≥6），nh=3，check(3)→未碎（3<5）；
    2. 步长ti=2，nh=3+2=5，check(5)→打碎（5=5）；
    3. 步长ti=1，从5-1=4开始查，check(4)→未碎（4<5）；
    4. 确定k=5，猜测次数3（3、5、4）。

2. （1.5分）不管输入的n和k具体为多少，t=2时的猜测数总是小于等于t=1时的猜测数

• 选项：正确/错误
• 答案：正确
• 解析：
  • t=1（线性）最坏需n次（k=n时，从1猜到n）；
  • t=2（最优）基于鸡蛋掉落问题的最优策略，猜测次数为O(√n)（如n=100时最多14次），远小于线性查找的n次；
    故t=2的猜测数始终≤t=1。

3. （1.5分）不管t=1或t=2，程序都一定会猜到正确结果

• 选项：正确/错误
• 答案：正确
• 解析：
  • t=1：线性遍历1~n，必能找到k（k≤n）；
  • t=2：最优策略通过步长调整覆盖1~n的所有楼层，且鸡蛋打碎后线性查找剩余区间，必能找到k；
    故程序一定能猜到正确结果。

4. （3分）函数guess1在运行过程中，cnt_broken的值最多为

• 选项：A.0 B.1 C.2 D.n
• 答案：B（1）
• 解析：guess1的逻辑是“第一次打碎即停止”：
  • 当猜到k层时，check(k)返回true（打碎），随后调用assert_ans(k)并返回，不会继续猜测；
  • 故cnt_broken最多为1（仅打碎1个鸡蛋）。

5. （3分）函数guess2在运行过程中，最多使用的猜测次数的量级为

• 选项：A.O(√n) B.O(n²) C.O(n) D.O(log n)
• 答案：A（O(√n)）
• 解析：guess2的步长由公式w*(w+1)/2 ≥n推导，解得w≈√(2n)，故猜测次数的量级为O(√n)（如n=100时w=14，n=1000时w=45）。

6. （3分）当输入的n=100的时候，代码中t=1和t=2分别需要的猜测次数最多分别为

• 选项：A.100,14 B.100,13 C.99,14 D.99,13
• 答案：A（100,14）
• 解析：
  • t=1（线性）：最坏情况k=100，需从1猜到100，猜测次数100；
  • t=2（最优）：找最大w使w*(w+1)/2 ≥100，解得w=14（14×15/2=105≥100），故最多猜测次数14。

第三题：分治求解方程解数

完整程序

#include <algorithm>
#include <cstdio>
#include <string>
#include <vector> 
#define ll long long
int n, m;                  // n=变量个数，m=每个变量的取值范围（1~m）
std::vector<int> k, p;     // k：变量系数数组；p：变量指数数组
int cnt1 = 0, cnt2 = 0;    // ans1、ans2的元素计数
std::vector<int> ans1, ans2;// 分治后两部分的“部分和”数组
std::vector<int> cntans1;  // ans1去重后的计数数组

// 快速幂函数：计算x^exp（原文档参数名k改为exp，避免与全局k冲突）
inline int mpow(int x, int exp) {
    int ans = 1;
    for (; exp; exp = exp >> 1, x = x * x) {  
        if (exp & 1) {  // 指数为奇数时，乘当前x
            ans = ans * x;
        }
    }
    return ans;
}

// DFS生成部分和：计算第l到r个变量的“k[i] * x_i^p[i]”之和
// ans：存储所有可能的部分和；cnt：计数ans的元素个数；l/r：变量范围；v：当前累加和
inline void dfs(std::vector<int>& ans, int& cnt, int l, int r, int v) {
    if (l > r) {  // 递归终止：已处理完l到r的所有变量
        ans.push_back(v);
        cnt++;
        return;
    }
    // 遍历变量x_i的所有可能值（1~m，因题目中x_i为正整数）
    for (int i = 1; i <= m; ++i) {
        // 计算当前项：k[l] * (i^p[l])，递归处理下一个变量
        dfs(ans, cnt, l + 1, r, v + k[l] * mpow(i, p[l]));
    }
    return;
}

int main() {
    scanf("%d%d", &n, &m);  // 输入变量个数n、每个变量的取值范围（1~m）
    k.resize(n + 1);        // 变量从1开始索引（与DFS的l/r对应）
    p.resize(n + 1);
    for (int i = 1; i <= n; ++i) {
        scanf("%d%d", &k[i], &p[i]);  // 输入第i个变量的系数k[i]和指数p[i]
    }

    // 分治：将n个变量拆分为前半部分（1~n/2）和后半部分（n/2+1~n）
    dfs(ans1, cnt1, 1, n >> 1, 0);    // 生成前半部分的所有部分和（S1）
    dfs(ans2, cnt2, (n >> 1) + 1, n, 0);  // 生成后半部分的所有部分和（S2）

    // 对前半部分ans1去重并统计每个部分和的出现次数（避免重复计算）
    std::sort(ans1.begin(), ans1.end());  // 排序使相同元素相邻
    int newcnt1 = 1;
    cntans1.push_back(1);  // 初始第一个元素的计数为1
    for (int i = 1; i < cnt1; ++i) {     
        if (ans1[i] == ans1[newcnt1 - 1]) {  // 与当前去重后最后一个元素相同
            cntans1[newcnt1 - 1]++;          // 计数+1
        } else {
            ans1[newcnt1++] = ans1[i];       // 新增不同元素
            cntans1.push_back(1);            // 新元素计数初始为1
        }
    }
    cnt1 = newcnt1;  // 更新ans1去重后的长度

    // 对后半部分ans2排序（用于双指针查找）
    std::sort(ans2.begin(), ans2.end());

    // 双指针查找：统计S1 + S2 = 0 的组合数（即S1 = -S2）
    int las = 0;          // ans1的左指针（从0开始）
    ll total_ans = 0;     // 总解数（用long long避免溢出）
    for (int i = cnt2 - 1; i >= 0; --i) {  // 从ans2的末尾（最大元素）向前遍历
        // 移动las，找到所有ans1[las] < -ans2[i] 的位置
        while (las < cnt1 && ans1[las] < -ans2[i]) {
            las++;
        }
        // 若ans1[las] == -ans2[i]，累加该部分和的出现次数
        if (las < cnt1 && ans1[las] == -ans2[i]) {
            total_ans += cntans1[las];
        }
    }

    printf("%lld\n", total_ans);  // 输出方程的总解数
    return 0;
}

程序功能分析

该程序采用分治策略求解「带系数和指数的整数方程解数」问题，核心目标是计算满足方程 (\sum_{i=1}^n k_i \cdot x_i^{p_i} = 0) 的解的数量（其中 (x_i \in [1,m])，k_i为系数，p_i为指数），步骤如下：

1. 分治拆分：将n个变量拆分为前半部分（1_{n/2）和后半部分（n/2+1}n），降低问题规模；
2. DFS生成部分和：通过DFS遍历每个变量的所有取值（1~m），生成两部分的“部分和”（S1=前半部分和，S2=后半部分和）；
3. 去重与排序：对S1去重并统计每个值的出现次数（减少重复计算），对S2排序（为双指针查找做准备）；
4. 双指针统计解数：方程 (\sum_{i=1}^n k_i x_i^{p_i}=0) 等价于 (S1 + S2 = 0)（即 (S1 = -S2)），通过双指针快速查找每个S2对应的-S2在S1中的出现次数，累加得到总解数。

题目解析（6个小题）

1. （1.5分）删除第51行的“std::sort(ans2.begin(), ans2.end());”后，代码输出的结果不会受到影响

• 选项：正确/错误
• 答案：错误
• 解析：第51行对ans2排序是双指针查找的前提：
  • 双指针逻辑依赖“ans2从大到小遍历”和“ans1从小到大排序”，若ans2无序，无法通过移动las指针（从左到右）高效找到 (S1 = -S2) 的位置；
  • 例如ans2无序时，可能错过部分 (S2) 对应的 (S1)，导致统计的解数偏少，输出结果改变。

2. （1.5分）假设计算过程中不发生溢出，函数mpow(x,k)的功能是求出 (x - k) 的取值

• 选项：正确/错误
• 答案：错误
• 解析：mpow是快速幂函数，核心逻辑是通过二进制拆分指数（右移操作）高效计算 (x^{exp})：
  • 例如mpow(2,3) = 2^3 = 8，而非2-3=-1；
  • 函数功能是计算 (x) 的 (exp) 次幂，而非 (x - k)。

3. （1.5分）代码中第39行到第50行的目的是为了将ans1数组进行“去重”操作

• 选项：正确/错误
• 答案：正确
• 解析：第39-50行的逻辑的核心是去重：
  1. 先对ans1排序（确保相同元素相邻）；
  2. 遍历ans1，若当前元素与去重后数组的最后一个元素相同，则计数+1（统计出现次数）；否则新增元素并初始化计数为1；
  3. 最终得到“去重后的ans1”和“每个元素的出现次数数组cntans1”，避免后续双指针查找时重复统计相同S1的次数。

4. （3分）当输入为“3 1 5 1 2 -1 2 1”时，输出结果为

• 选项：A.4 B.8 C.0 D.10
• 答案：C（0）
• 解析：输入参数解析：n=3（3个变量），m=1（每个x_i只能取1），k=[5,2,2]（系数），p=[1,-1,1]（指数），方程为 (5x_1^1 + 2x_2^{-1} + 2x_3^1 = 0)：
  1. 变量取值：x1=x2=x3=1（仅1种可能）；
  2. 计算部分和：
     • 前半部分（1~1个变量）：S1 = 5×1^1 = 5；
     • 后半部分（2~3个变量）：S2 = 2×1^(-1) + 2×1^1 = 2+2=4；
  3. 方程验证：S1 + S2 = 5+4=9≠0，无满足条件的解，总解数为0。

5. （3分）记程序结束前p数组元素的最大值为P，则该代码的时间复杂度是

• 选项：A.O(n) B.O(m^n log m^n) C.O(m^(n/2) log m^(n/2)) D.O(m^(n/2) (log m^(n/2) + log P))
• 答案：D
• 解析：时间复杂度由三部分构成：
  1. DFS生成部分和：每个变量有m种取值，分治后两部分各有n/2个变量，每部分的时间为O(m^{(n/2))，总DFS时间O(m}(n/2))；
  2. 快速幂计算：mpow函数的时间为O(log P)（P是p数组最大值，指数最大为P），每个DFS调用执行一次mpow，故这部分时间为O(m^(n/2) log P)；
  3. 排序与去重：ans1和ans2的长度均为m^{(n/2)，排序时间为O(m}(n/2) log m^(n/2))；
     综上，总时间复杂度为O(m^(n/2) (log m^(n/2) + log P))。

6. （3分）本题所求出的是

• 选项：A.满足 (a,b,c \in [1,m]) 的整数方程 (a^3 + b^3 = c^3) 的解的数量 B.满足 (a,b,c \in [1,m]) 的整数方程 (a^2 + b^2 = c^2) 的解的数量 C.满足 (x_i \in [0,m]) 的整数方程 (\sum_{i=1}^n k_i \cdot x_i^{p_i} = 0) 的解的数量 D.满足 (x_i \in [1,m]) 的整数方程 (\sum_{i=1}^n k_i \cdot x_i^{p_i} = 0) 的解的数量
• 答案：D
• 解析：
  • 选项A/B：方程仅含3个变量且指数固定（3或2），与程序中“n个变量、任意指数p_i”不符，排除；
  • 选项C：x_i的取值范围是[0,m]，但程序DFS中x_i从1开始遍历（for(int i=1;i<=m;++i)），即x_i∈[1,m]，排除；
  • 选项D：与程序功能完全一致（n个变量x_i∈[1,m]，求解 (\sum_{i=1}^n k_i x_i^{p_i}=0) 的解数），正确。

三、完善程序（共30分）

第一题：特殊最短路（最多一条免费边）

完整题目

给定一个含N个点、M条边的带权无向图，边权非负。起点为S，终点为T。对于一条S到T的路径，可以在整条路径中至多选择一条边作为“免费边”：当第一次经过这条被选中的边时，费用视为0；如果之后再次经过该边，则仍按其原始权重计费（点和边均允许重复经过）。求从S到T的最小总费用。
以下代码求解了上述问题，试补全程序。

#include <algorithm>
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
const long long INF = 1e18;  // 无穷大（表示不可达）

// 边结构：to=目标节点，weight=边权重
struct Edge {
    int to;
    int weight;
};

// 优先队列状态：dist=当前距离，u=当前节点，used_freebie=是否使用过免费边（0=未用，1=已用）
struct State {
    long long dist;
    int u;
    int used_freebie;
    // 优先队列按距离升序排列（小根堆），重载>运算符
    bool operator>(const State &other) const {
        return dist > other.dist;
    }
};

int main() {
    int n, m, s, t;
    cin >> n >> m >> s >> t;  // 输入节点数n、边数m、起点s、终点t
    vector<vector<Edge>> adj(n + 1);  // 邻接表存储无向图
    for (int i = 0; i < m; ++i) {
        int u, v, w;
        cin >> u >> v >> w;
        adj[u].push_back({v, w});  // 无向图，双向加边
        adj[v].push_back({u, w});
    }

    // 距离数组：d[u][0]=未用免费边到u的最短距离；d[u][1]=已用免费边到u的最短距离
    vector<vector<long long>> d(n + 1, vector<long long>(2, INF));
    priority_queue<State, vector<State>, greater<State>> pq;  // 小根堆（Dijkstra算法）

    d[s][0] = 0;  // 起点s未用免费边，距离为0
    pq.push({0, s, ①});  // 初始状态：距离0，节点s，未用免费边

    while (!pq.empty()) {
        State current = pq.top();
        pq.pop();
        long long dist = current.dist;
        int u = current.u;
        int used = current.used_freebie;

        // 若当前状态的距离大于已知最短距离，跳过（冗余状态）
        if (dist > ②) {
            continue;
        }

        // 遍历当前节点的所有邻边，进行松弛操作
        for (const auto &edge : adj[u]) {
            int v = edge.to;
            int w = edge.weight;

            // 情况1：不使用免费边，正常累加边权
            if (d[u][used] + w < ③) {
                ③ = d[u][used] + w;
                pq.push({③, v, used});
            }

            // 情况2：使用免费边（仅当未用免费边时），权重视为0
            if (used == 0) {
                if (④ < d[v][1]) {
                    d[v][1] = ④;
                    pq.push({d[v][1], v, 1});
                }
            }
        }
    }

    // 终点T的最小距离为“未用免费边”和“已用免费边”的最小值
    cout << ⑤ << endl;
    return 0;
}

程序功能分析

该程序是带状态的Dijkstra算法，用于解决“最多一条免费边”的最短路径问题，核心思路：

1. 状态扩展：在传统Dijkstra的基础上增加“是否使用免费边”的状态（used_freebie），用二维距离数组d[u][0/1]存储两种状态下的最短距离；
2. 松弛操作分两种情况：
   • 不使用免费边：正常累加边权，更新同一状态（used）下的距离；
   • 使用免费边：仅当未使用过免费边（used=0）时，将当前边权视为0，更新“已使用免费边”状态（d[v][1]）的距离；
3. 结果取最小值：终点T的最小距离为两种状态（用或不用免费边）的距离最小值，确保覆盖所有可能的最优路径。

填空解析（5个小题）

1. ①处应填

• 选项：A.0 B.1 C.-1 D.false
• 答案：A（0）
• 解析：初始状态为“起点s，未使用免费边”，根据used_freebie的定义（0=未用，1=已用），此处应填0。

2. ②处应填

• 选项：A.d[j][used] B.d[u][used] C.d[t][used] D.INF
• 答案：B（d[u][used]）
• 解析：Dijkstra算法中，若当前弹出的状态距离dist大于已知的最短距离（d[u][used]），则该状态是冗余的（已找到更优路径），直接跳过。

3. ③处应填

• 选项：A.d[v][1] B.d[v][used] C.d[u][used] D.d[v][0]
• 答案：B（d[v][used]）
• 解析：该分支是“不使用免费边”的松弛操作：从节点u到v，边权为w，需更新v节点在“同一使用状态（used）”下的最短距离，即d[v][used]。

4. ④处应填

• 选项：A.d[v][0] B.d[v][1] C.d[u][0] D.d[u][1]
• 答案：C（d[u][0]）
• 解析：该分支是“使用免费边”的松弛操作：
  • 仅当used=0（未使用过免费边）时，可将当前边权视为0；
  • 此时v节点“已使用免费边”的距离（d[v][1]）= u节点“未使用免费边”的距离（d[u][0]），无需加边权w。

5. ⑤处应填

• 选项：A.d[t][1] B.d[t][0] C.min(d[t][0], d[t][1]) D.d[t][0] + d[t][1]
• 答案：C（min(d[t][0], d[t][1])）
• 解析：终点T的最小距离需比较两种状态的结果：
  • d[t][0]：未使用免费边到T的最短距离；
  • d[t][1]：已使用免费边到T的最短距离；
    取两者最小值即为最终答案。

第二题：缺陷生产线测试

完整题目

工厂有n条生产线（编号0~n-1），已知恰有一条存在缺陷。每一轮测试为：从若干生产线的产品取样混合成一个批次发给客户，若批次含缺陷产品则退货（结果记为1），否则正常收货（结果记为0）。限制：所有批次中最多只能有k次退货（结果1的次数≤k）。目标：设计最少的测试轮数w，保证根据反馈结果唯一确定缺陷生产线。
程序包含三部分：①确定最小w；②生成最优测试方案；③根据测试结果推断缺陷生产线。程序确定w最小值的方法为：由于不同的生产线故障时，测试应当返回不同的结果，因此w轮测试的可能结果数不应少于生产线数量。
test_subset()函数为抽象测试接口，输入所有批次的方案并返回一个二进制编码；该编码表示为每批次的检测结果（即最低位是第1批次、最高位是第w批次）；其实现在此处未给出。试补全程序。

待补全程序（修正语法错误后）

#include <algorithm>
#include <cstddef>
#include <iostream>
#include <vector>
using namespace std;

// 计算组合数C(w,i)：从w个批次中选i个批次返回1的方案数
long long comb(int w, int i) {
    if (i < 0 || i > w) return 0;
    long long res = 1;
    for (int t = 1; t <= i; ++t) {
        res = res * (w - t + 1) / t;  // 组合数公式：C(w,i)=w!/(i!(w-i)!)
    }
    return res;
}

// 计算w轮测试的可能结果数（最多k次1）
long long count_patterns(int w, int k) {
    long long total = 0;
    for (int t = 0; t <= min(w, k); ++t) {
        total += comb(w, t);  // 累加C(w,0)~C(w,k)（t=1的次数）
    }
    return total;
}

// 抽象测试接口：输入测试方案，返回反馈的二进制编码（最低位=第1批次）
int test_subset(const vector<vector<int>> &plan);

int solve(int n, int k) {
    // 第1步：确定最小w（结果数≥n）
    int w = 1;
    while (①) {  // 若当前w的结果数< n，需增大w
        ++w;
    }
    cout << w << endl;

    // 第2步：生成每个生产线的二进制编码（1的个数≤k，确保唯一）
    vector<vector<int>> code(n, vector<int>(w, 0));  // code[j][i]：第j条线第i批次的编码位
    int idx = 0;  // 当前生产线索引（0~n-1）
    vector<int> bits(w, 0);  // 存储二进制编码（长度w）
    for (int ones = 0; ones <= k && idx < n; ++ones) {  // ones=编码中1的个数（0~k）
        // 设置bits前ones位为1，其余为0（初始编码）
        fill(bits.begin(), bits.end(), 0);
        fill(bits.begin(), bits.begin() + ones, 1);
        do {
            // 将当前bits赋值给第idx条生产线的编码
            for (int b = 0; b < w; ++b) {
                code[idx][b] = bits[b];
            }
            idx++;
            if (idx >= n) break;  // 所有生产线已分配编码，退出
        } while (std::②);  // 生成下一个含ones个1的二进制编码
    }

    // 第3步：生成测试方案plan（plan[i]：第i批次包含的生产线）
    vector<vector<int>> plan(w);
    for (int i = 0; i < w; ++i) {  // i=批次号（0~w-1）
        for (int j = 0; j < n; ++j) {  // j=生产线号（0~n-1）
            if (③) {  // 若第j条线在第i批次的编码位为1，加入该批次
                plan[i].push_back(j);
            }
        }
    }

    // 第4步：调用测试接口，获取反馈编码signature
    int signature = test_subset(plan);

    // 第5步：解码反馈编码，得到每批次的结果sig_bits
    vector<int> sig_bits(w, 0);
    for (int i = 0; i < w; ++i) {
        if (④) {  // 提取signature的第i位（最低位=第0位）
            sig_bits[i] = 1;
        }
    }

    // 第6步：匹配编码，找到缺陷生产线（编码与sig_bits一致）
    for (int j = 0; j < n; ++j) {
        if (⑤) {  // 第j条线的编码与反馈结果一致
            return j;
        }
    }
    return -1;  // 理论上不会到达此处（题目保证恰有一条缺陷线）
}

int main() {
    int n, k;
    cin >> n >> k;  // 输入生产线数量n、最多退货次数k
    int ans = solve(n, k);  // 求解缺陷生产线编号
    cout << ans << endl;
    return 0;
}

程序功能分析

该程序基于编码理论设计缺陷生产线测试方案，核心逻辑是通过“唯一的二进制编码”区分每条生产线，步骤如下：

1. 确定最小测试轮数w：w轮测试中，“最多k次1”的二进制编码总数（组合数之和）需≥n（确保每条生产线有唯一编码）；
2. 生成编码与测试方案：为每条生产线分配唯一的二进制编码（1的个数≤k），plan[i]存储“第i批次包含的生产线”（编码第i位为1的生产线）；
3. 测试与解码：调用test_subset()获取反馈的二进制编码，解码后与生产线编码匹配，找到唯一对应的缺陷生产线。

填空解析（5个小题）

1. ①处应填

• 选项：A.(1<<w)<n B.count_patterns(w,k)<n C.count_patterns(k,w)<n D.comb(w,k)<n
• 答案：B（count_patterns(w,k)<n）
• 解析：count_patterns(w,k)计算w轮测试、最多k次1的编码总数，当总数< n时，说明编码不足以区分n条生产线，需增大w，直到总数≥n。

2. ②处应填

• 选项：A.next_permutation(bits.begin(), bits.end()) B.prev_permutation(bits.begin(), bits.end()) C.next_permutation(bits.begin(), bits.begin()+ones) D.prev_permutation(bits.begin(), bits.begin()+ones)
• 答案：A（next_permutation(bits.begin(), bits.end())）
• 解析：next_permutation生成当前数组的“下一个字典序排列”，用于遍历所有“含ones个1”的二进制

【CSP-J&CSP-S第二轮免费公益模拟赛】
CSP-J＆S 2025 模拟赛是免费开放，共10套，赛后有详细解析，想参加的学生请联系。
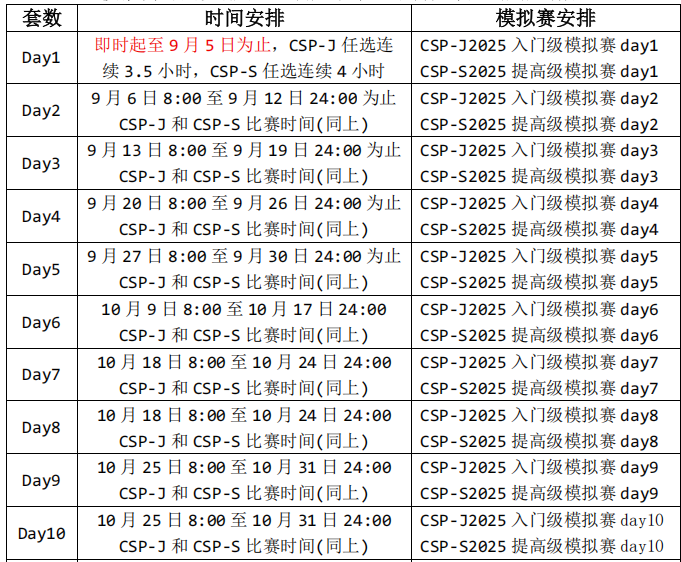
模拟赛具体安排：