雅克比迭代法与高斯塞德尔迭代法求解方程组（C语言）

分别用雅可比 迭代法与高斯塞德尔迭代法解下列方程组：

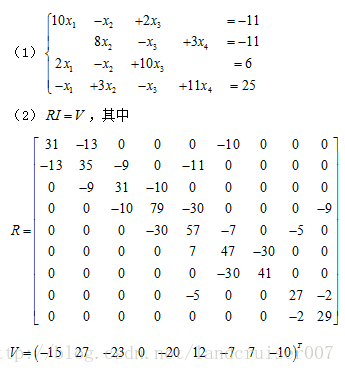
雅可比迭代法：

#include<stdio.h>
#include<math.h>
#define eps 1e-6
#define max 100
//雅可比迭代法
void jacobi(float *a,int n,float x[])
{
    int i,j,k=0;
    float epsilon,s;
    float *y=new float[n];
    for(i=0;i<n;i++)x[i]=0;
    while(1)
    {
        epsilon=0;
        k++;
        for(i=0;i<n;i++)
        {
            s=0;
            for(j=0;j<n;j++)
            {
                if(j==i)continue;
                s+=*(a+i*(n+1)+j)*x[j];
            }
            y[i]=(*(a+i*(n+1)+n)-s)/(*(a+i*(n+1)+i));
            epsilon+=fabs(y[i]-x[i]);
        }
        for(i=0;i<n;i++)x[i]=y[i];
        if(epsilon<eps)
        {
            printf("%d\n",k);return;}
        if(k>=max)
        {printf("fasan");return;}
    }
    delete y;
}

void main()
{
    int i;
    float a[4][5]={10,-1,2,0,-11,
                   0,8,-1,3,-11,
                   2,-1,10,0,6,
                   -1,3,-1,11,25};
    float x[4];
    jacobi(a[0],4,x);
    for(i=0;i<4;i++)printf("x[%d]=%f\n",i+1,x[i]);

    float b[9][10]={31,-13,0,0,0,-10,0,0,0,-15,
                   -13,35,-9,0,-11,0,0,0,0,27,
                   0,-9,31,-10,0,0,0,0,0,-23,
                   0,0,-10,79,-30,0,0,0,-9,0,
                   0,0,0,-30,57,-7,0,-5,0,-20,
                   0,0,0,0,7,47,-30,0,0,12,
                   0,0,0,0,0,-30,41,0,0,-7,
                   0,0,0,0,-5,0,0,27,-2,7,
                   0,0,0,0,0,0,0,-2,29,-10};
    float xx[9];
    jacobi(b[0],9,xx);
    for(i=0;i<9;i++)printf("xx[%d]=%f\n",i+1,xx[i]);
}

高斯赛德尔迭代法：

#include<stdio.h>
#include<math.h>
#define N 500
//高斯塞德尔
void gauss(float *a,int n,float x[])
{
    int i,j,k=1;
    float d,dx,eps;
    for(i=0;i<=n-1;i++)x[i]=0.0;
    while(1)
    {
        eps=0;
        for(i=0;i<=n-1;i++)
        {
            d=0;
            for(j=0;j<=n-1;j++)
            {
                if(j==i)continue;
                d+=*(a+i*(n+1)+j)*x[j];
            }
            dx=(*(a+i*(n+1)+n)-d)/(*(a+i*(n+1)+i));
            eps+=fabs(dx-x[i]);
            x[i]=dx;
        }
        if(eps<1e-6)
        {printf("%d\n",k);return;}
        if(k>N)
        {
            printf("fasan\n");
            return;
        }
        k++;
    }
}

void main()
{
    int i;
    float a[4][5]={10,-1,2,0,-11,
                   0,8,-1,3,-11,
                   2,-1,10,0,6,
                   -1,3,-1,11,25};
    float x[4];
    float b[9][10]={31,-13,0,0,0,-10,0,0,0,-15,
                   -13,35,-9,0,-11,0,0,0,0,27,
                   0,-9,31,-10,0,0,0,0,0,-23,
                   0,0,-10,79,-30,0,0,0,-9,0,
                   0,0,0,-30,57,-7,0,-5,0,-20,
                   0,0,0,0,7,47,-30,0,0,12,
                   0,0,0,0,0,-30,41,0,0,-7,
                   0,0,0,0,-5,0,0,27,-2,7,
                   0,0,0,0,0,0,0,-2,29,-10};
    float xx[9];
    gauss(a[0],4,x);
    for(i=0;i<4;i++)printf("x[%d]=%f\n",i+1,x[i]);

    gauss(b[0],9,xx);
    for(i=0;i<9;i++)printf("xx[%d]=%f\n",i+1,xx[i]);
}