贝叶斯定理[编辑]
贝叶斯定理(Bayes' theorem)是概率论中的一个结果,它跟随机变量的条件概率以及边缘概率分布有关。在有些关于概率的解说中,贝叶斯定理(贝叶斯更新)能够告知我们如何利用新证据修改已有的看法。
通常,事件A在事件B(发生)的条件下的概率,与事件B在事件A的条件下的概率是不一样的;然而,这两者是有确定的关系,贝叶斯定理就是这种关系的陈述。贝叶斯公式的用途在于通过己知三个概率函数推出第四个。它的内容是:在B出现的前提下,A出现的概率等于A出现的前提下B出现的概率乘以A出现的概率再除以B出现的概率。通过联系A与B,计算从一个事件产生另一事件的概率,即从结果上溯原。
作为一个普遍的原理,贝叶斯定理对于所有概率的解释是有效的;然而,频率主义者和贝叶斯主义者对于在应用中,某个随机事件的概率该如何被赋值,有着不同的看法: 频率主义者根据随机事件发生的频率,或者总体样本里面的发生的个数来赋值概率;贝叶斯主义者则根据未知的命题来赋值概率。这样的理念导致贝叶斯主义者有更多的机会使用贝叶斯定理。
目录
[隐藏]陈述[编辑]
贝叶斯定理是关于随机事件A和B的条件概率(或边缘概率)的一则定理。
其中P(A|B)是在B发生的情况下A发生的可能性。
在贝叶斯定理中,每个名词都有约定俗成的名称:
- P(A)是A的先验概率或边缘概率。之所以称为"先验"是因为它不考虑任何B方面的因素。
- P(A|B)是已知B发生后A的条件概率,也由于得自B的取值而被称作A的后验概率。
- P(B|A)是已知A发生后B的条件概率,也由于得自A的取值而被称作B的后验概率。
- P(B)是B的先验概率或边缘概率,也作标准化常量(normalized constant).
按这些术语,Bayes定理可表述为:
- 后验概率 = (相似度*先验概率)/标准化常量
也就是说,后验概率与先验概率和相似度的乘积成正比。
另外,比例P(B|A)/P(B)也有时被称作标准相似度(standardised likelihood),Bayes定理可表述为:
- 后验概率 = 标准相似度*先验概率
从条件概率推导贝叶斯定理[编辑]
根据条件概率的定义。在事件B发生的条件下事件A发生的概率是
-
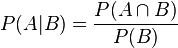 。
。
同样地,在事件A发生的条件下事件B发生的概率
整理与合并这两个方程式,我们可以找到
这个引理有时称作概率乘法规则。上式两边同除以P(B),若P(B)是非零的,我们可以得到贝叶斯 定理:
二中择一的形式[编辑]
贝叶斯定理通常可以再写成下面的形式:
-
 ,
,
其中AC是A的补集(即非A)。故上式亦可写成:
在更一般化的情况,假设{Ai}是事件集合里的部份集合,对于任意的Ai,贝叶斯定理可用下式表示:
以可能性与相似率表示贝叶斯定理[编辑]
其中
定义为B发生时,A发生的可能性(odds);
则是A发生的可能性。相似率(Likelihood ratio)则定义为:
贝叶斯定理与概率密度[编辑]
贝叶斯定理亦可用于连续机率分布。由于机率密度函数严格上并非机率,由机率密度函数导出贝叶斯定理观念上较为困难(详细推导参阅[1])。贝叶斯定理与机率密度的关系是由求极限的方式建立:
全机率定理则有类似的论述:
如同离散的情况,公式中的每项均有名称。 f(x, y)是X和Y的联合分布; f(x|y)是给定Y=y后,X的后验分布; f(y|x)= L(x|y)是Y=y后,X的相似度函数(为x的函数); f(x)和f(y)则是X和Y的边际分布; f(x)则是X的先验分布。 为了方便起见,这里的f在这些专有名词中代表不同的函数(可以由引数的不同判断之)。
贝叶斯定理的推广[编辑]
对于变量有二个以上的情况,贝式定理亦成立。例如:
这个式子可以由套用多次二个变量的贝式定理及条件机率的定义导出:
-

-
 。
。
一般化的方法则是利用联合机率去分解待求的条件机率,并对不加以探讨的变量积分(意即对欲探讨的变量计算边缘机率)。取决于不同的分解形式,可以证明某些积分必为1,因此分解形式可被简化。利用这个性质,贝叶斯定理的计算量可能可以大幅下降。贝叶斯网络为此方法的一个例子,贝叶斯网络指定数个变量的联合机率分布的分解型式,该机率分布满足下述条件:当其他变量的条件机率给定时,该变量的条件机率为一简单型式。
范例[编辑]
吸毒者检测[编辑]
贝叶斯定理在检测吸毒者时很有用。假设一个常规的检测结果的敏感度与可靠度均为99%,也就是说,当被检者吸毒时,每次检测呈阳性(+)的概率为99%。而被检者不吸毒时,每次检测呈阴性(-)的概率为99%。从检测结果的概率来看,检测结果是比较准确的,但是贝叶斯定理却可以揭示一个潜在的问题。假设某公司将对其全体雇员进行一次鸦片吸食情况的检测,已知0.5%的雇员吸毒。我们想知道,每位医学检测呈阳性的雇员吸毒的概率有多高?令“D”为雇员吸毒事件,“N”为雇员不吸毒事件,“+”为检测呈阳性事件。可得
- P(D)代表雇员吸毒的概率,不考虑其他情况,该值为0.005。因为公司的预先统计表明该公司的雇员中有0.5%的人吸食毒品,所以这个值就是D的先验概率。
- P(N)代表雇员不吸毒的概率,显然,该值为0.995,也就是1-P(D)。
- P(+|D)代表吸毒者阳性检出率,这是一个条件概率,由于阳性检测准确性是99%,因此该值为0.99。
- P(+|N)代表不吸毒者阳性检出率,也就是出错检测的概率,该值为0.01,因为对于不吸毒者,其检测为阴性的概率为99%,因此,其被误检测成阳性的概率为1-99%。
- P(+)代表不考虑其他因素的影响的阳性检出率。该值为0.0149或者1.49%。我们可以通过全概率公式计算得到:此概率 = 吸毒者阳性检出率(0.5% x 99% = 0.495%)+ 不吸毒者阳性检出率(99.5% x 1% = 0.995%)。P(+)=0.0149是检测呈阳性的先验概率。用数学公式描述为:
根据上述描述,我们可以计算某人检测呈阳性时确实吸毒的条件概率P(D|+):
尽管我们的检测结果可靠性很高,但是只能得出如下结论:如果某人检测呈阳性,那么此人是吸毒的概率只有大约33%,也就是说此人不吸毒的可能性比较大。我们测试的条件(本例中指D,雇员吸毒)越难发生,发生误判的可能性越大。











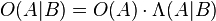
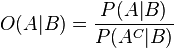

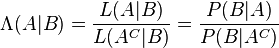
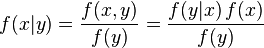
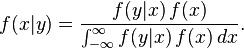
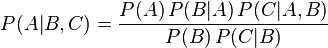

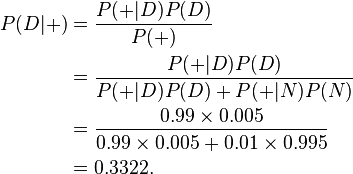














 8598
8598

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








