《数学要素》读书笔记

系统性的对数学知识做了整理，包括各种数学概念、生活中的数学知识、几何图形、中学年代的数学知识、大学年代的数理知识、机器学习算法中的数学概念、多维空间，通过各种各样的图对数学做了阐述，不再只是一个概念，更加具体和形象。

原文链接：https://www.zhihu.com/question/366915371/answer/31099661433

---

以下数书中的一些内容整理，供参考：

数学中的概念

数字，就是人类思想的空气，无处不在，不可或缺。已经融合到人类生活的方方面面，多数时候，数字像是空气，我们认为它理所应 当，甚至忽略了它的存在。

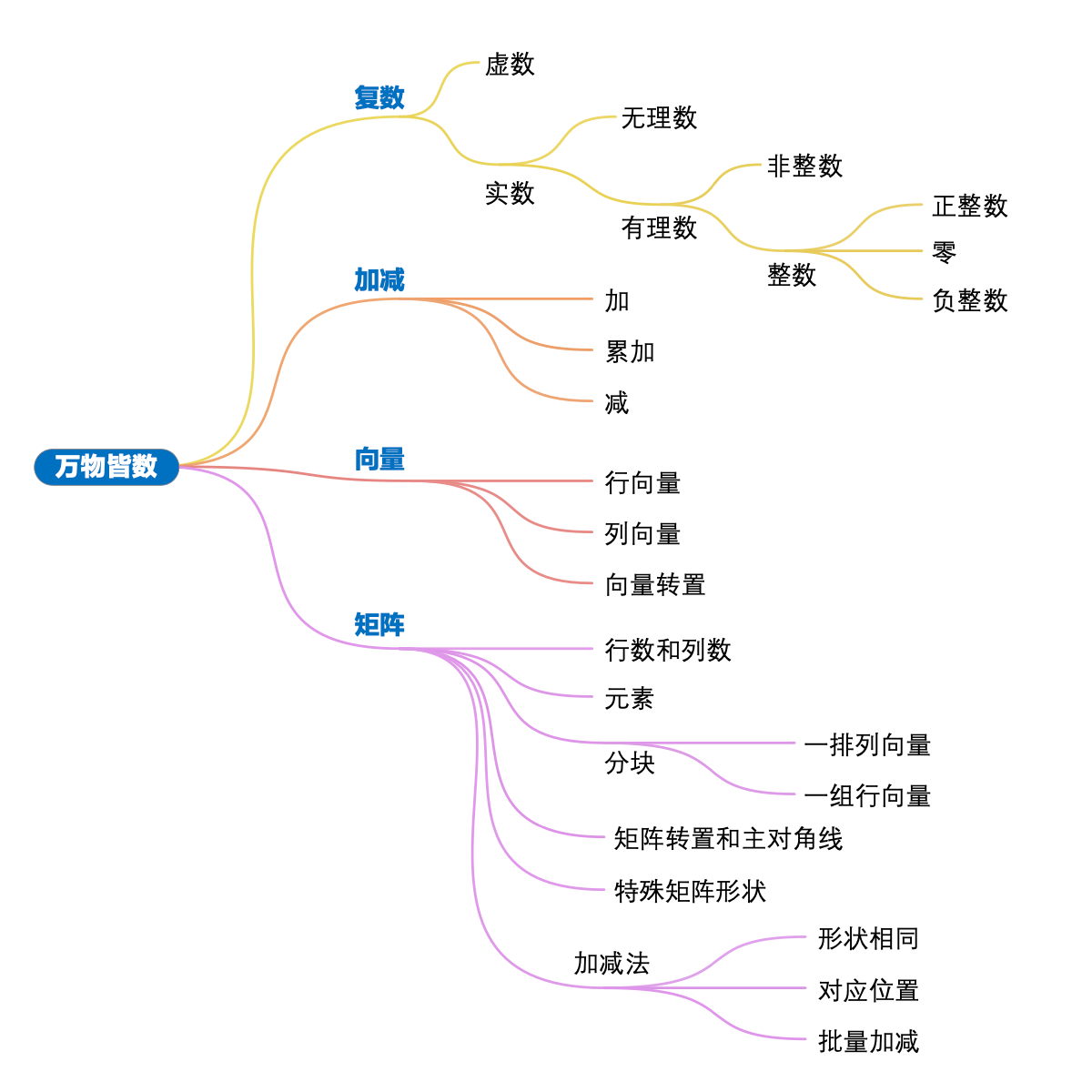
©️数的概念。

数学，不分种族、不分地域；对于数学来说，其文化世界自成一国。

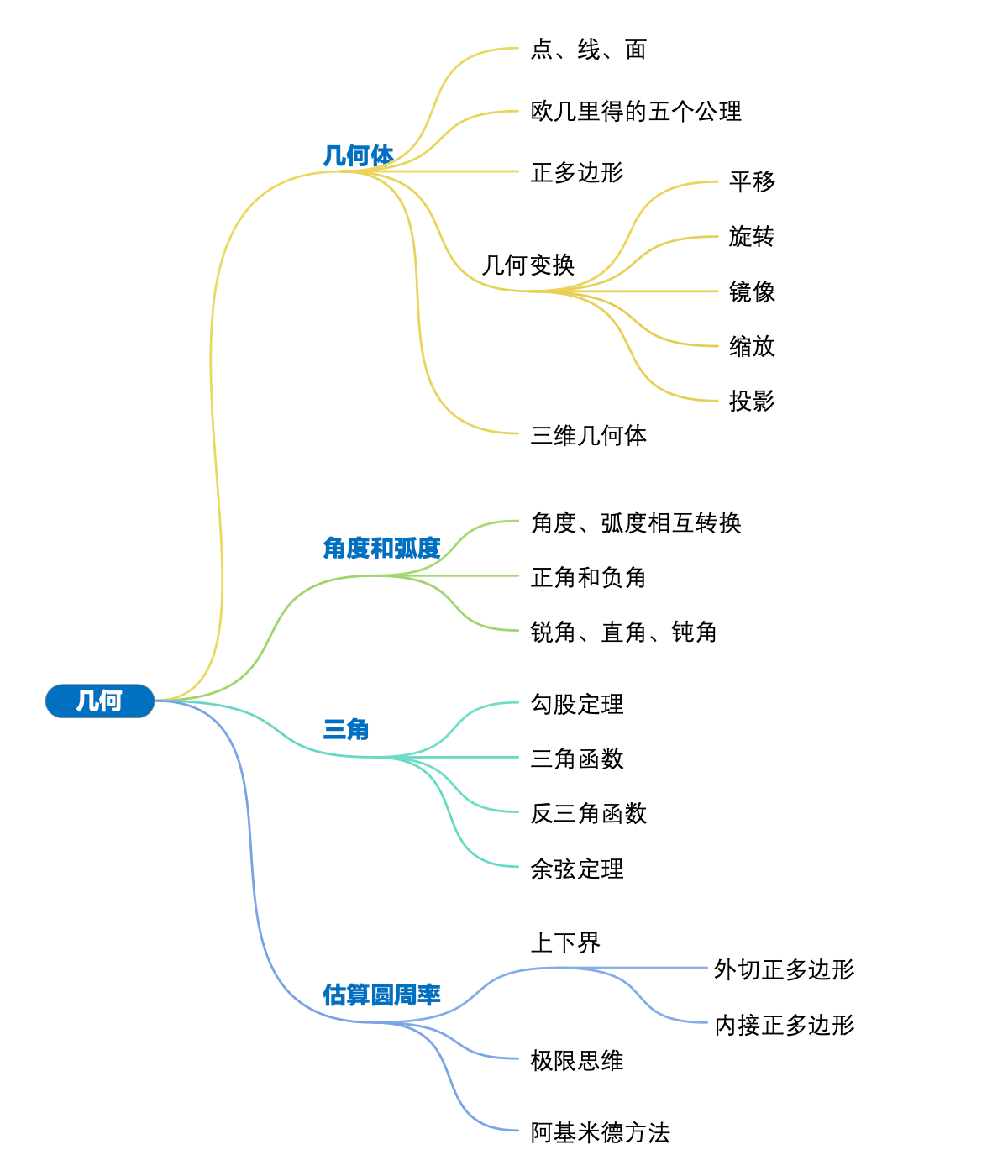
©️几何的概念。

音乐之美由耳朵来感受，几何之美让眼睛去欣赏

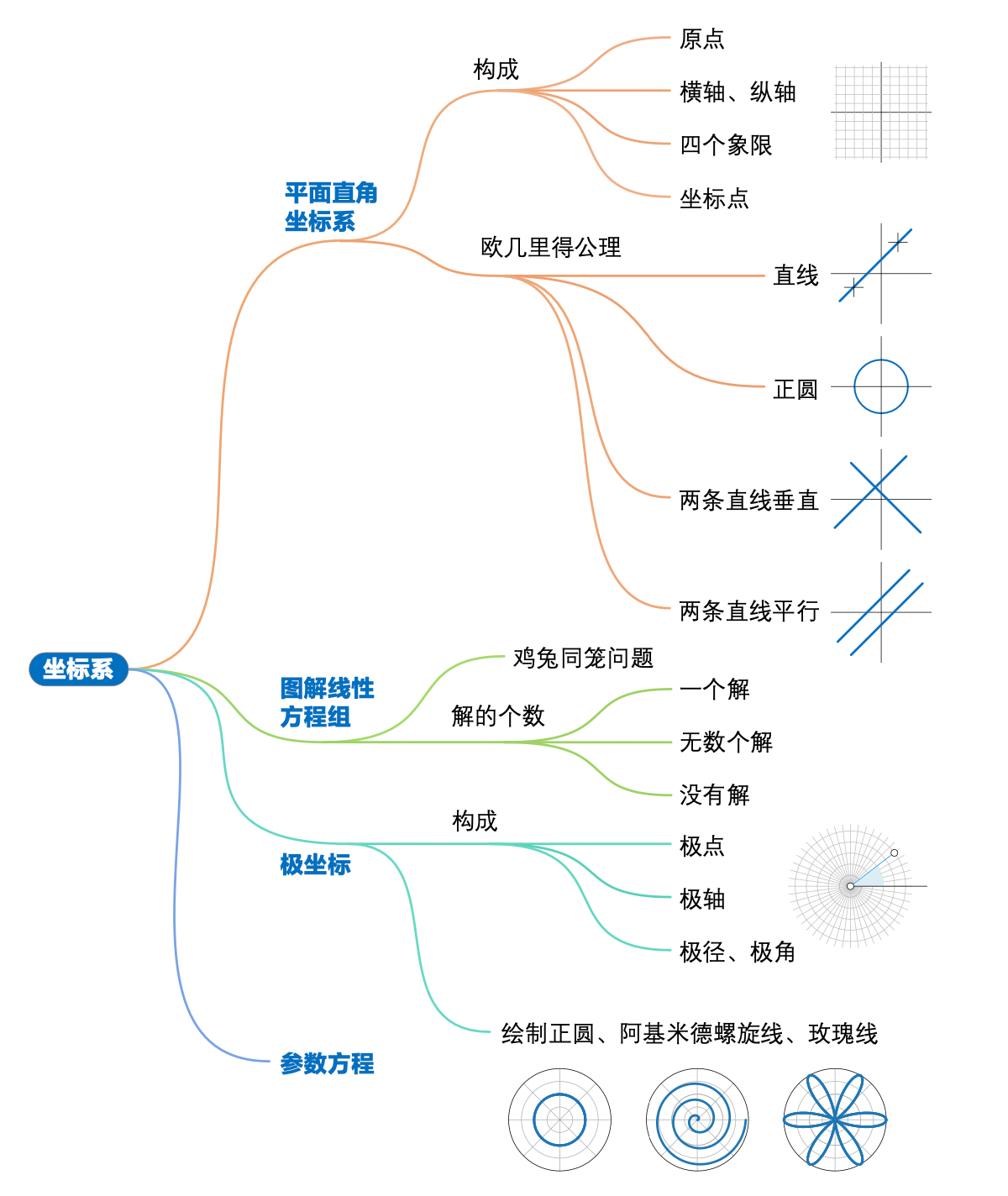
©️坐标系的概念。

笛卡尔坐标系，几何代数一相逢，便胜却人间无数

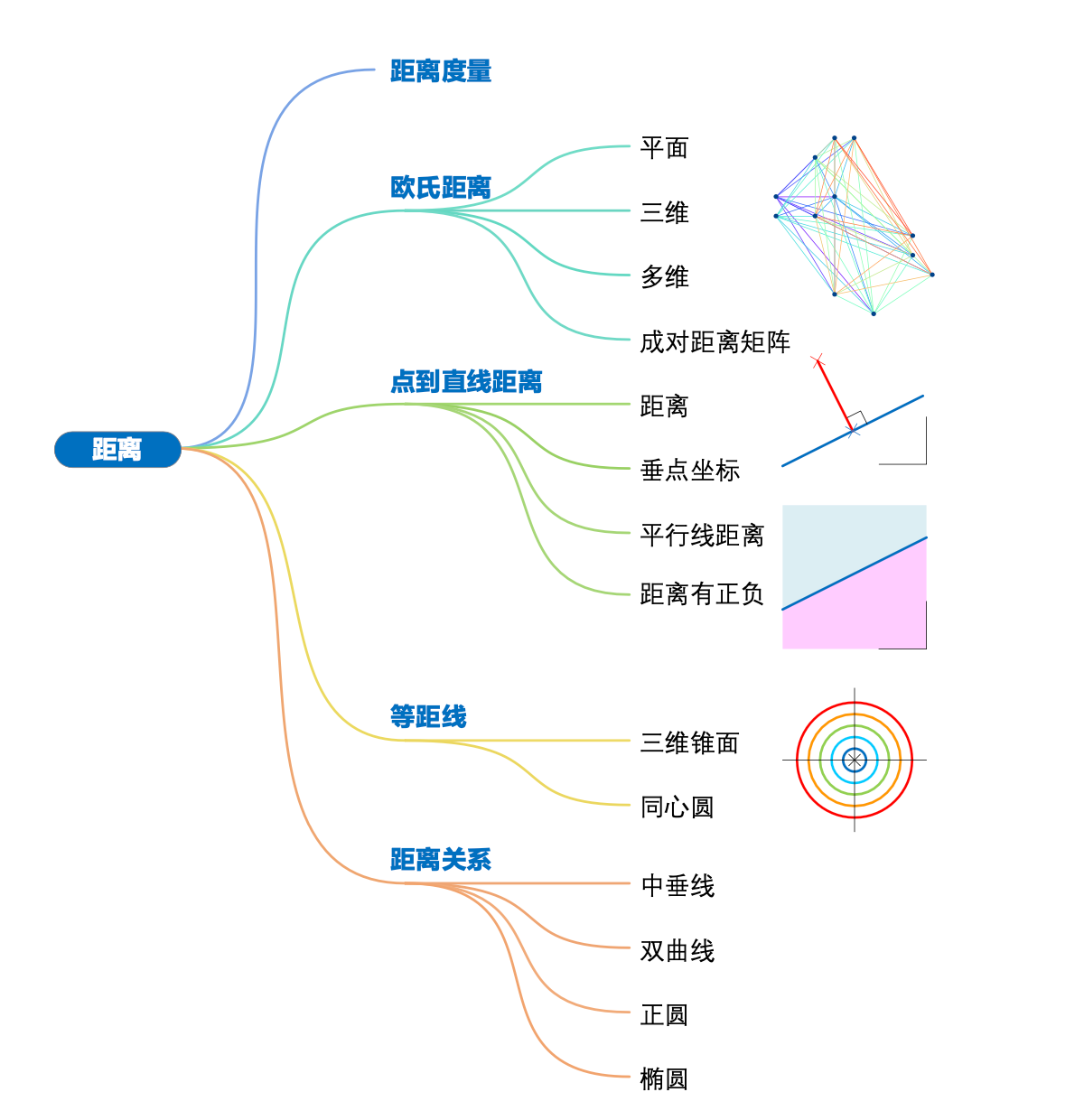
©️距离的概念。

人是万物的尺度，两点之间最短的路径是一条线段。

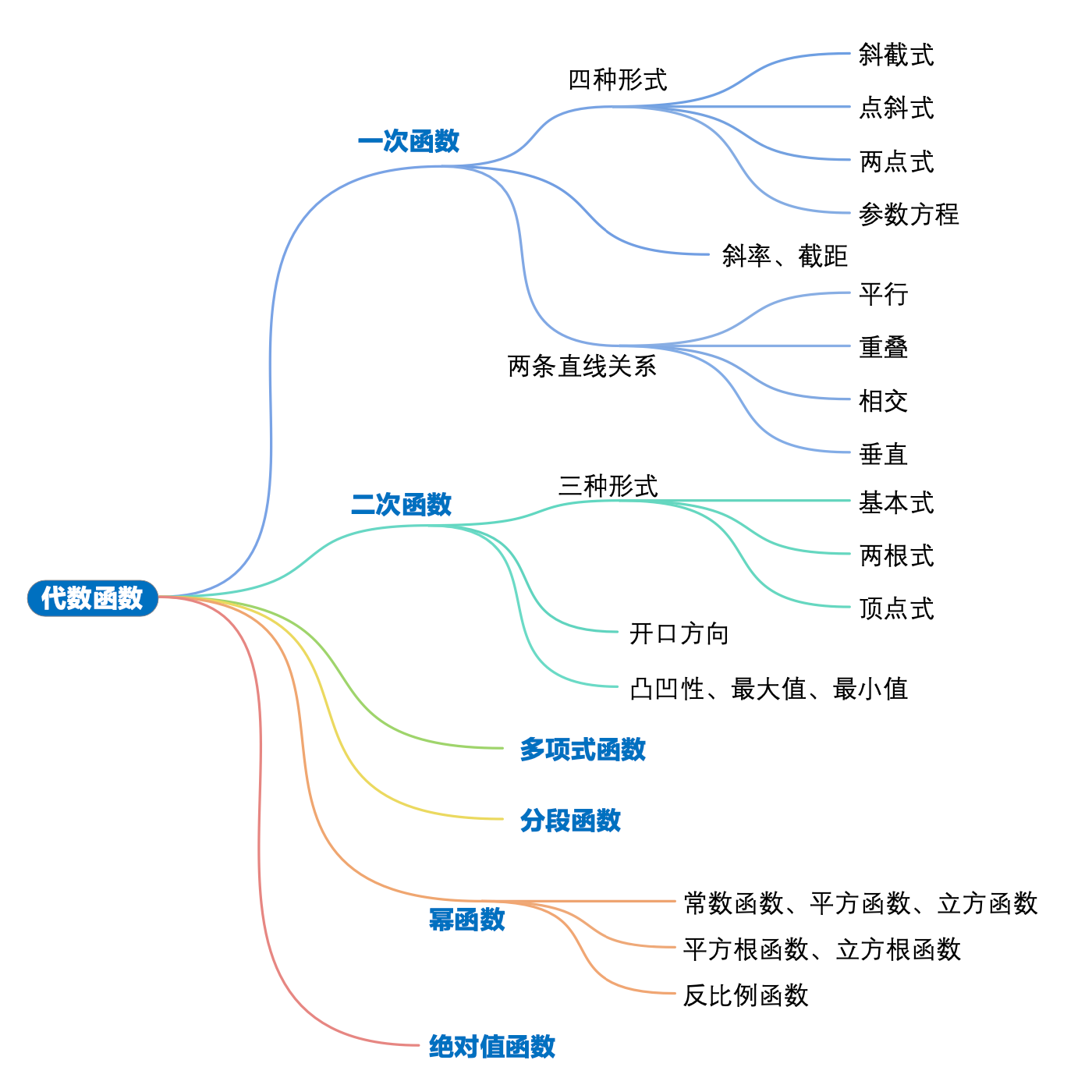
©️函数的概念。

代数函数，自变量有限次加、减、乘、除、有理指数幂和开方

---

生活中的数学

©️几何滥觞于田间地头。

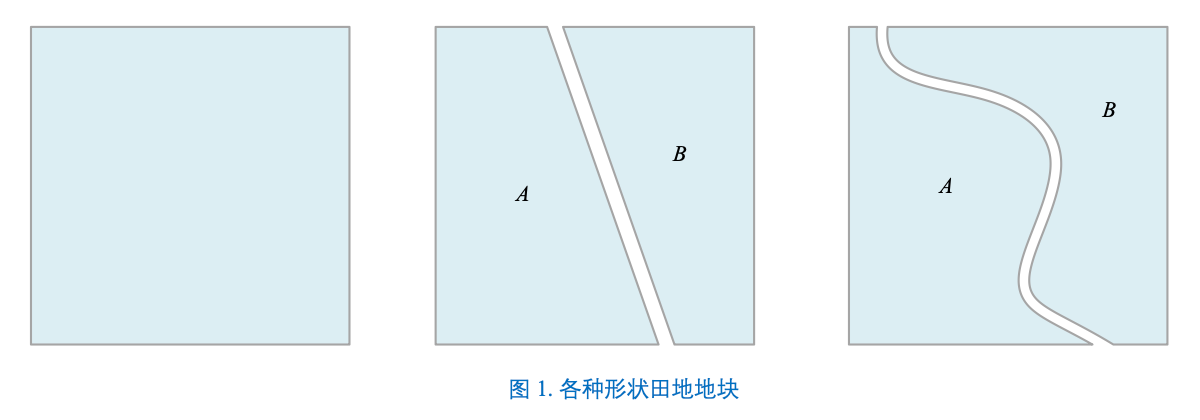
在古埃及，尼罗河每年都要淹没河两岸。当洪水退去，留下的肥沃土壤让河两岸平原的农作物生长。但是洪水同样冲走了标示不同耕地界桩。

法老每年都要派大量测量员重新丈量土地。测绘员们用打结的绳子去丈量土地和角度，以便 重置这些界桩。计算矩形、三角形农田面积当然简单。对于对于复杂的几何形体，测绘员经常将 土地分割成矩形和三角形来估算土地面积。古埃及的几何知识则随着测量精度提高而不断累积精进。

无独有偶，中国古代重要的数学典籍之一《九章算术》的第一章名为“方田”。这一章多数题 目以丈量土地为例，讲解如何计算长方形、三角形、梯形、圆形等等各式几何形状的面积。

©️咖啡杯在六个方向投影图像

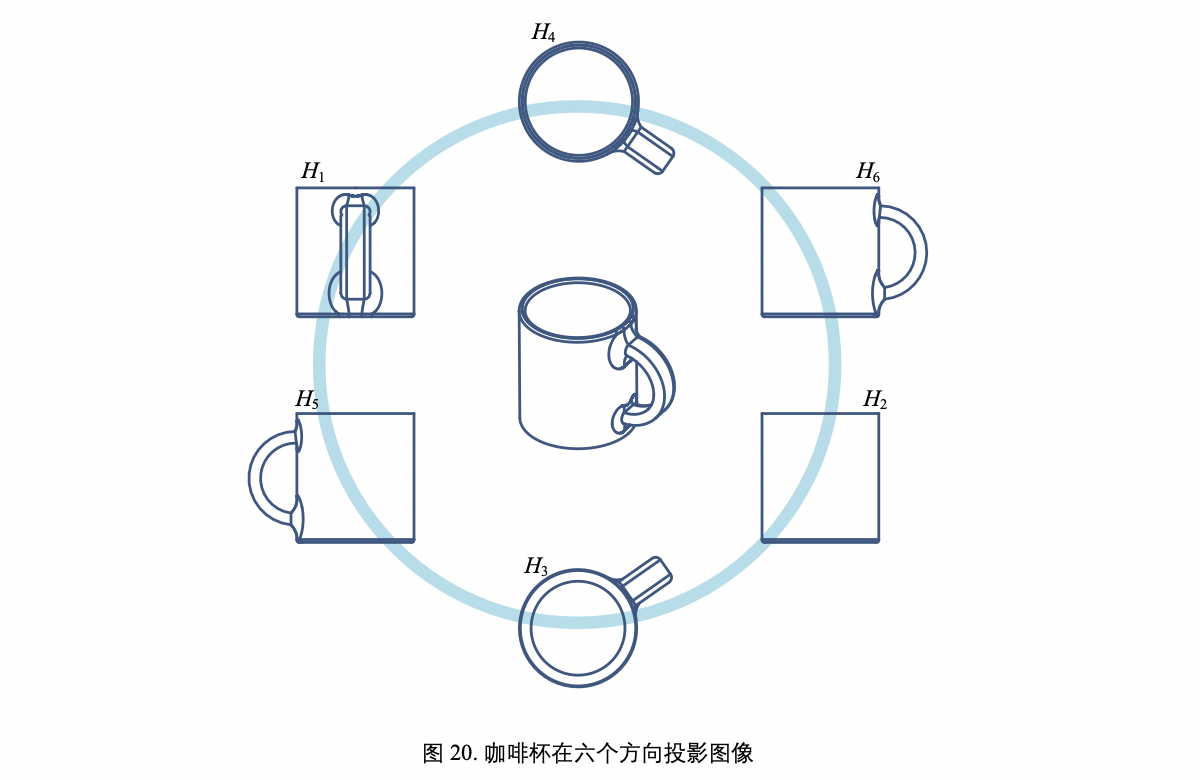
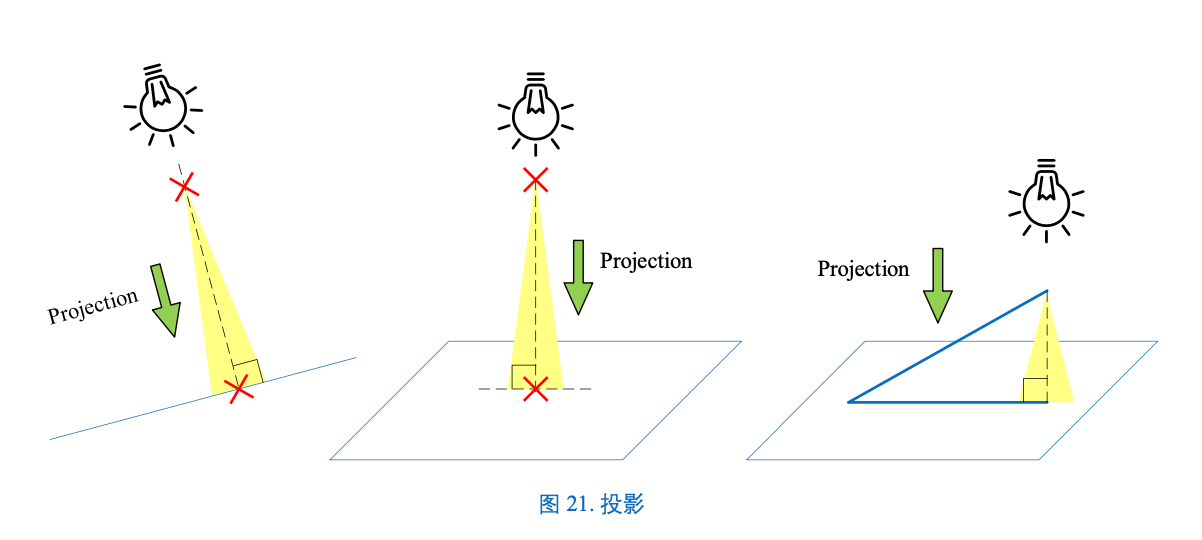
©️光照的投影

数学中最常见的投影是正投影。正投影中，投影线 (图 21 中虚线) 垂直于投影面。线性代数中，我们管这类投影叫正交投影 (orthogonal projection)

数学和几何图形

©️点和线

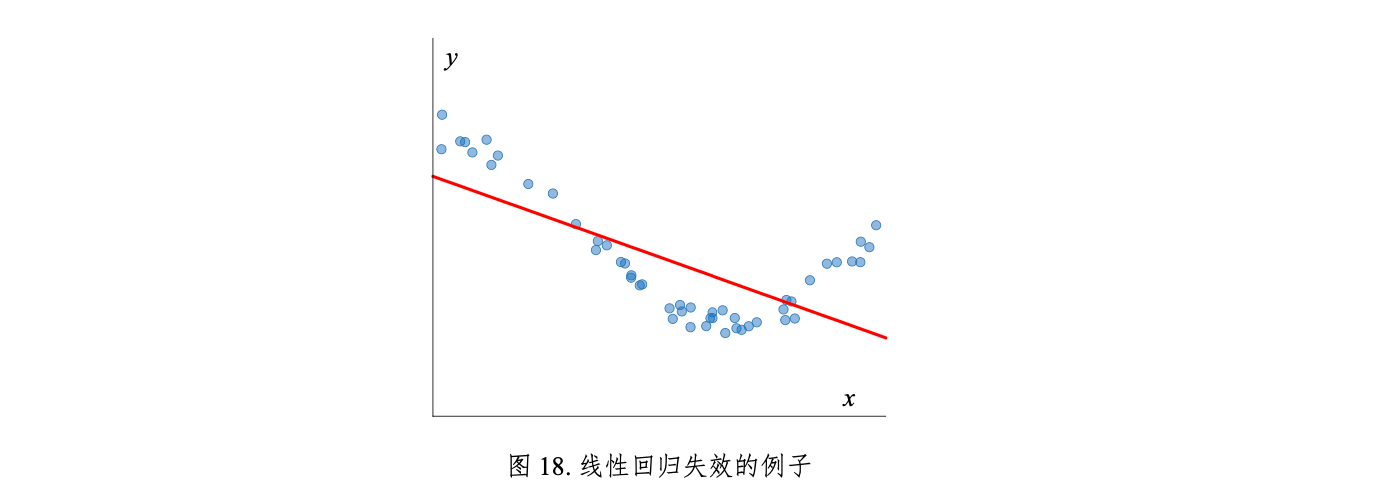
©️圆形

不同半径的圆形

©️抛物线

初等函数:数学模型的基础

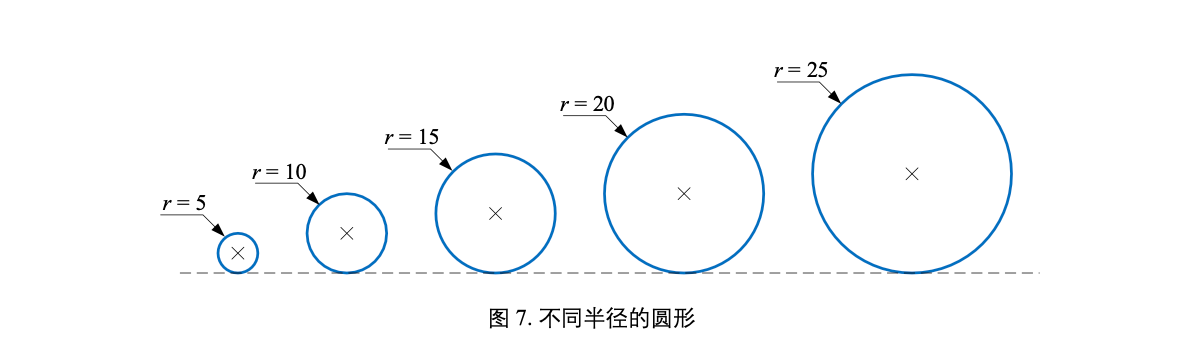
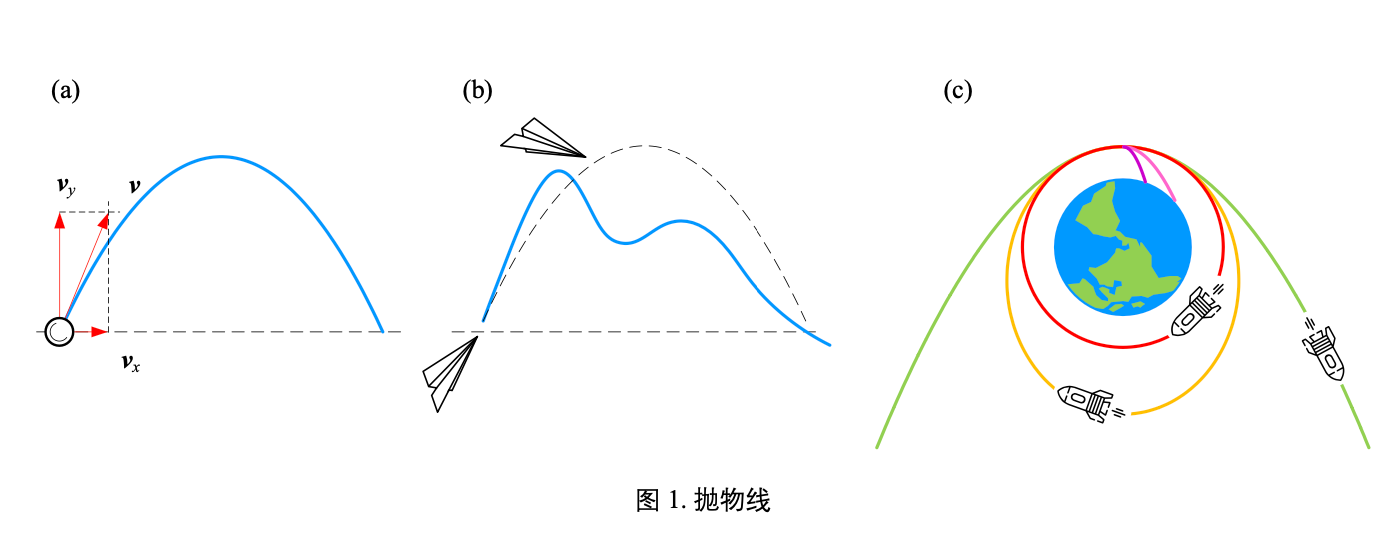
斜向上方抛起一个小球，忽略空气阻力影响，小球在空中划出的一道曲线就 可以用抛物线描述。这条抛物线就是二次函数。小球在空中不同时刻的位置，以及最终的落点， 都可以通过二次函数这个模型计算得到。

同样的仰角，斜向上抛出一个纸飞机，纸飞机在空中的飞行轨迹就不得不考虑纸飞机外形、 空气气流这些因素。如图 1 (b) 所示，抛物线已经不足以描述纸飞机的轨迹。

类似的，很多应用场景都需要对抛物线模型进行修正。比如，击打网球时，施加旋转可以改 变网球飞行轨迹。射击时，枪管膛线让子弹旋转飞行，这必然会让其行进轨迹发生变化。发射炮 弹时，空气阻力与炮弹外型和飞行速度有密切关系，这显然会影响炮弹飞行轨迹和落点。

此外，认为抛射物体轨迹为抛物线至少基于几个假设前提。比如，忽略空气阻力的影响;再比如，假设大地平坦;同时假设物体受到的地球引力垂直大地。

中学年代的数学

©️勾股定理

《周髀算经》编写于公元前一世纪之前，其中记录着商高与周公的一段对话。商高说“故折 矩，勾广三，股修四，经隅五。”后人把这一发现简化成——勾三、股四、弦五。《九章算术》的 最后一章讲解的也是勾股定理。

满足勾股定理的一组整数，比如 (3, 4, 5)，叫做勾股数。

在西方，勾股定理被称作毕达哥拉斯定理 (Pythagorean Theorem)。

古代很多文明都独立发现了勾股定理。原因也不难理解，古时人们在丈量土地，建造房屋 时，都离不开直角。

古埃及人善于使用绳索构造特定几何关系。比如，绳索等距打结，就可以充当带刻度的直 尺。绳索一端固定，另外一段绕固定端旋转一周，就可以得到正圆。

古埃及人也发现 3:4:5 的直角三角形。据此，利用绳索可以轻松获得直角。绳索等距打 13 个 结，形成 12 段等长线段。按照 3:4:5 比例分配等距线段，3 等分和 4 等分的两边的夹角便是直 角。

勾股定理的一般形式如下:

a2 +b2 =c2

如图 25 所示，a 和 b 为直角边，c 为斜边。图中，a2、b2、c2 分别为三个正方形的面积。

©️圆锥曲线

常见圆锥曲线参数方程

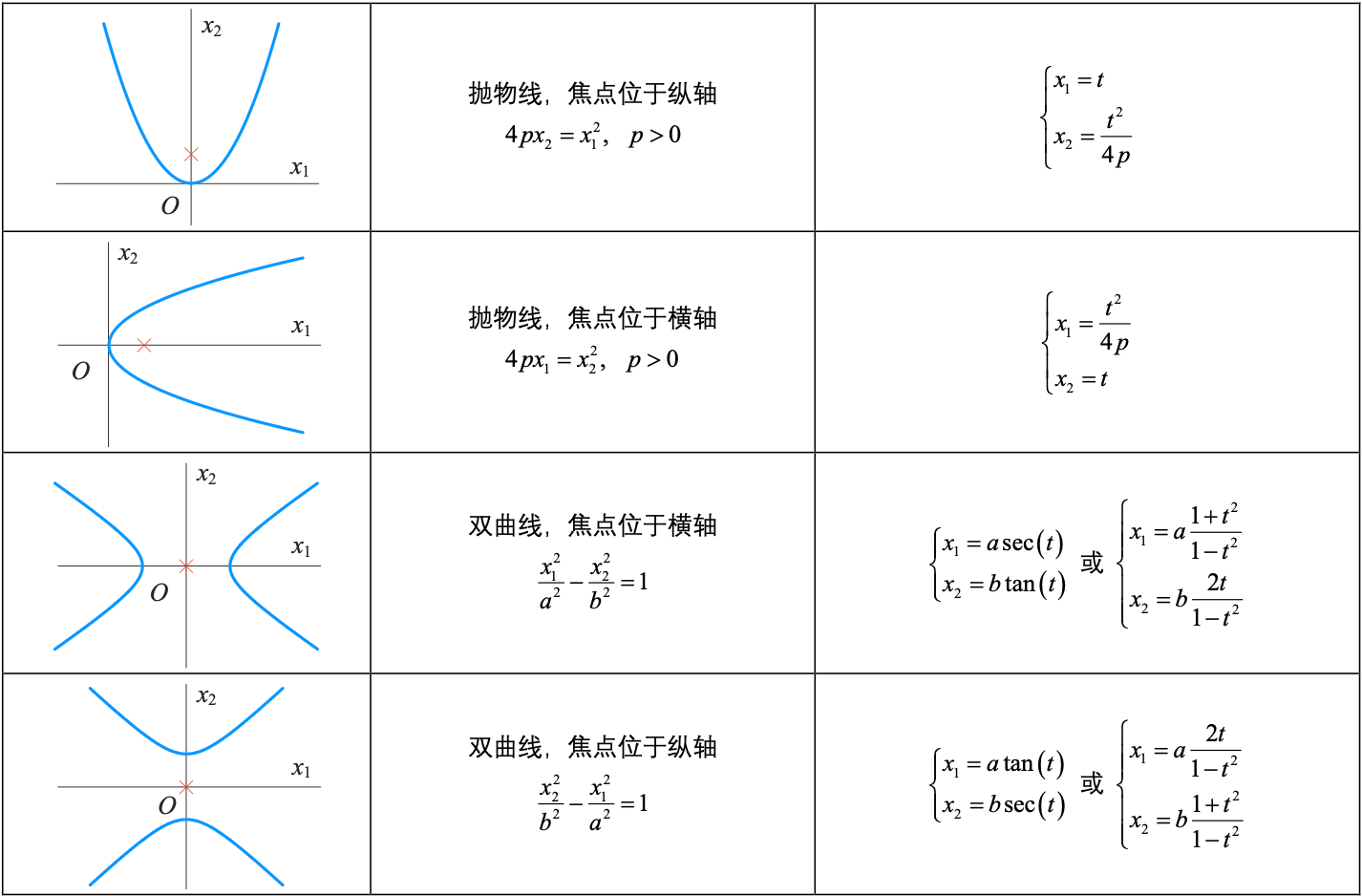
©️一次函数

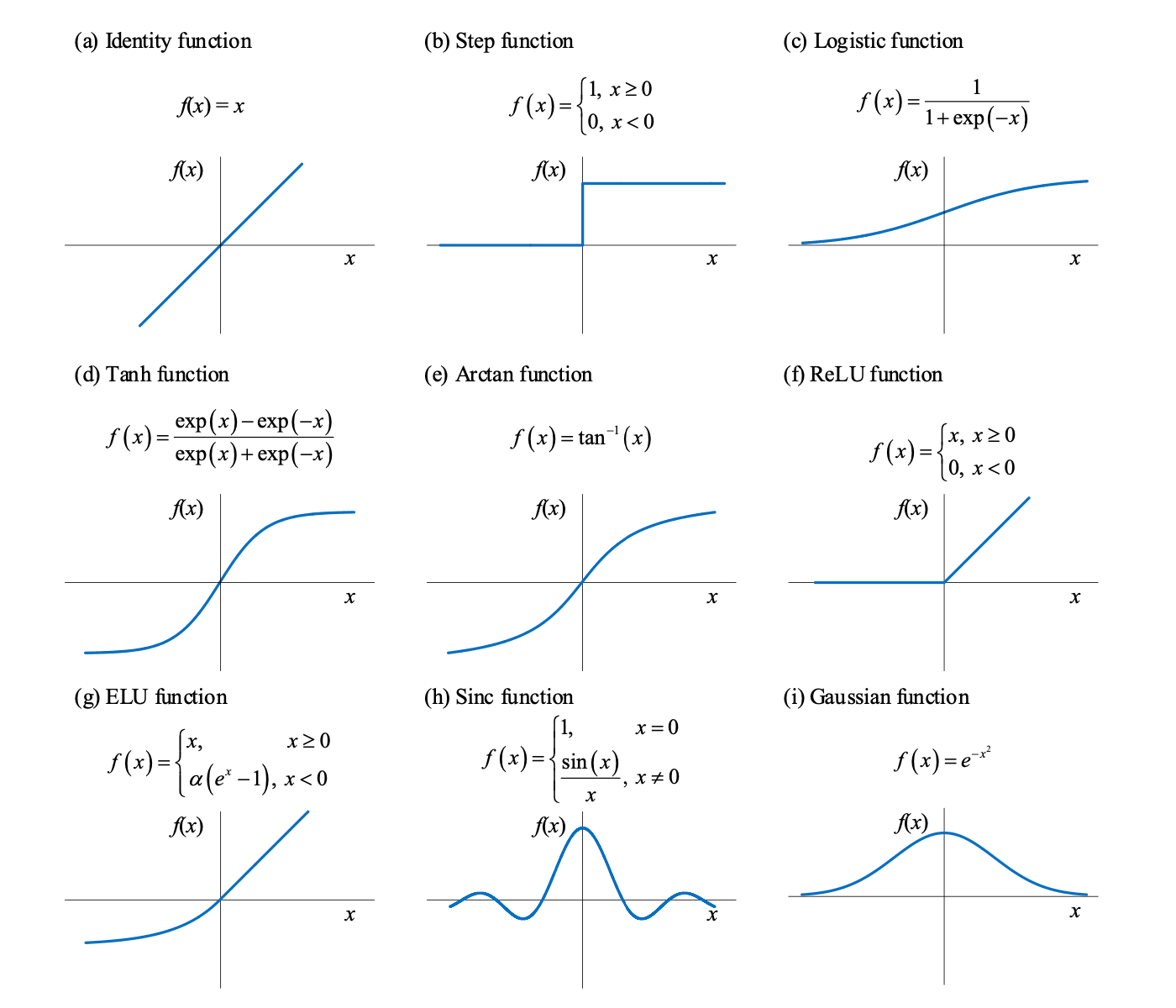
几种常见的判别函数 f(x) 及其对应图像

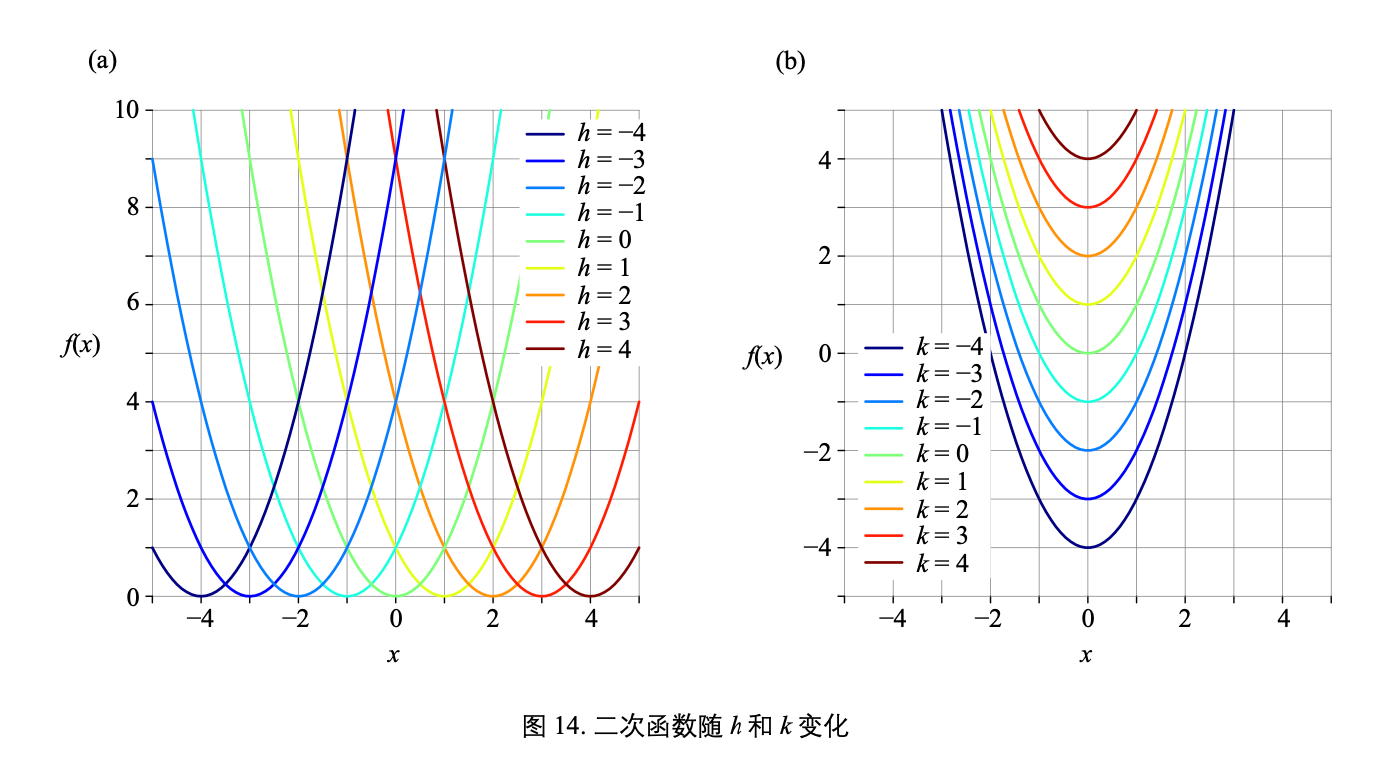
©️二次函数

图像开口大小随系数 a 变化。a 的绝对值越大，开口越小，对应二次函 数图像变化越剧烈。

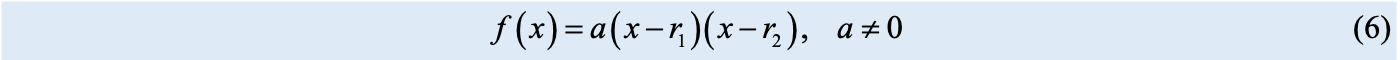
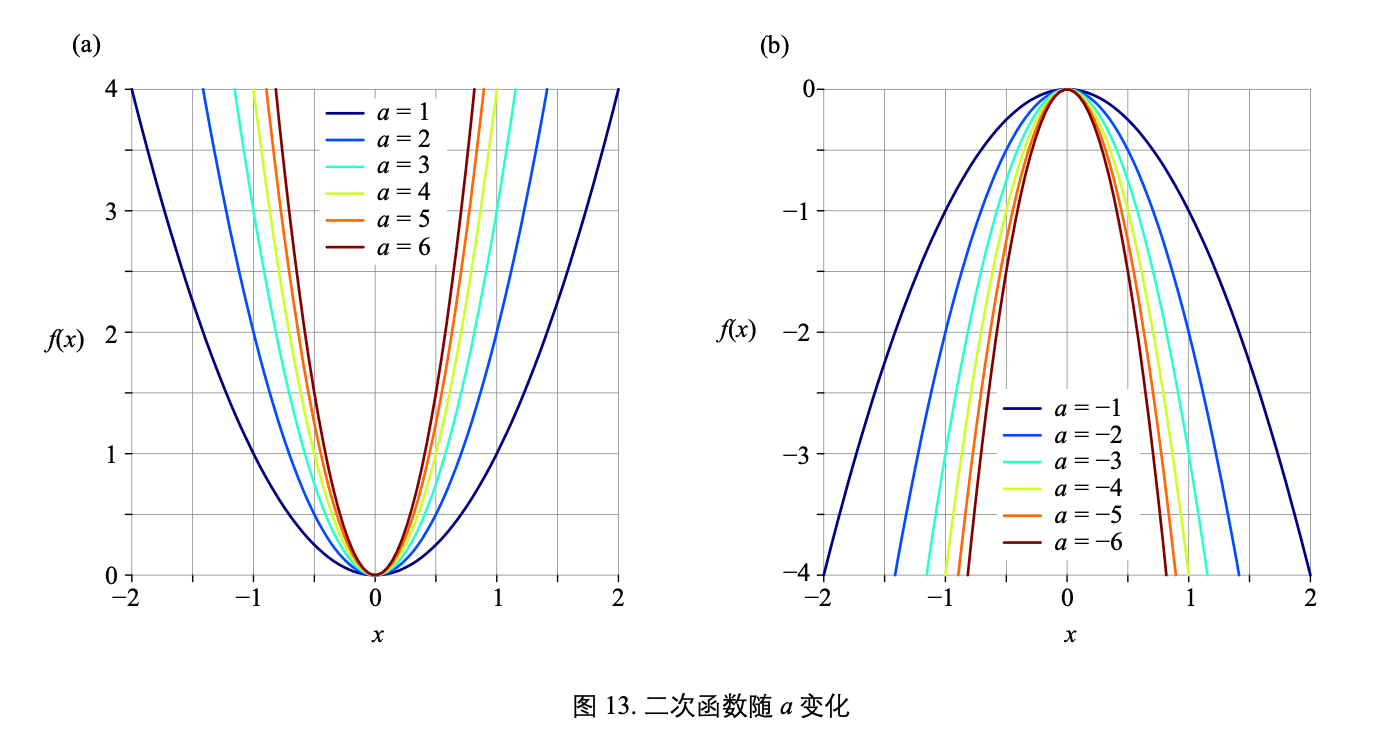
图 14 (a) 所示为函数图像和 h 的关系，显然 h 影响函数在水平方向位置。图 14 (b) 所示为函数 图像和 k 的关系，k 影响函数在竖直方向位置。

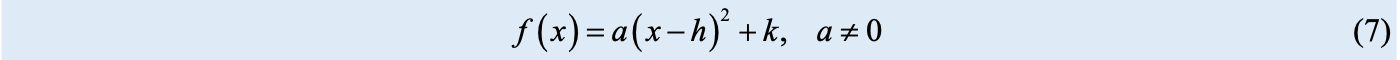
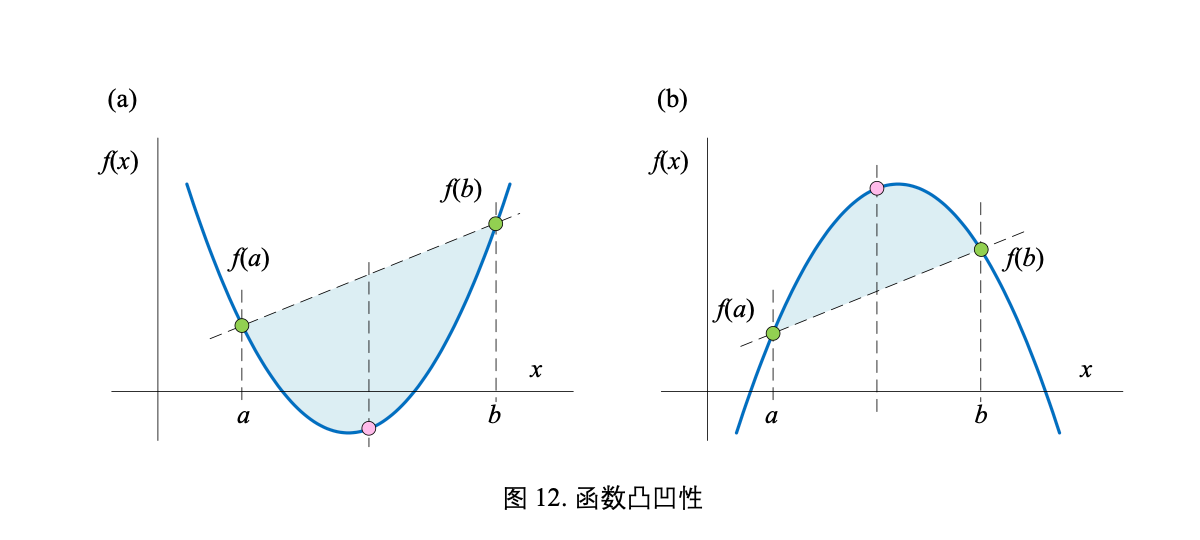
©️数学中的凸凹性

凸凹性，凸函数和凹函数

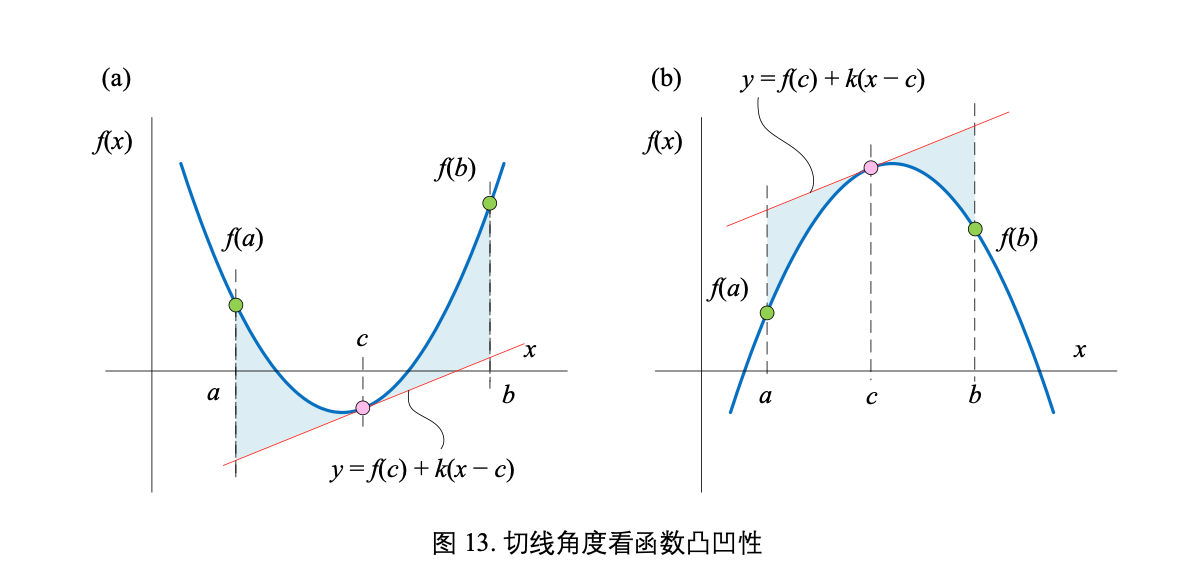
从切线角度来看函数凸凹性

y= f(c)+k(x−c)

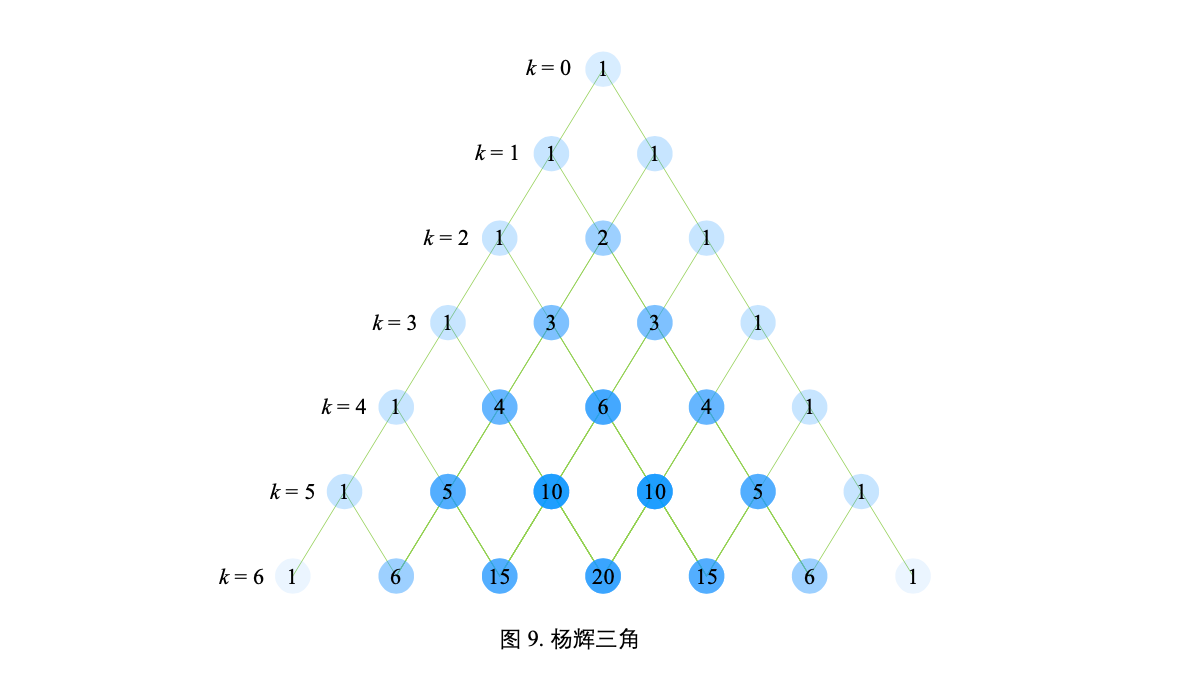
©️杨辉三角

几何、代数、概率等知识的有趣联系。

数学中的周期性

©️极值和最值

函数图像看成一座山峰，A、B、C、D、E、F 都是极值，即山峰和山谷的总和。其中，A、B、C 为极大值，即山峰;D、E、F 为极小值，即山谷。显然，B 是最高的山峰，也就是最大值，也叫全局最大值。而 E 是最低的山谷，也就是最小值，也叫全局最小值。

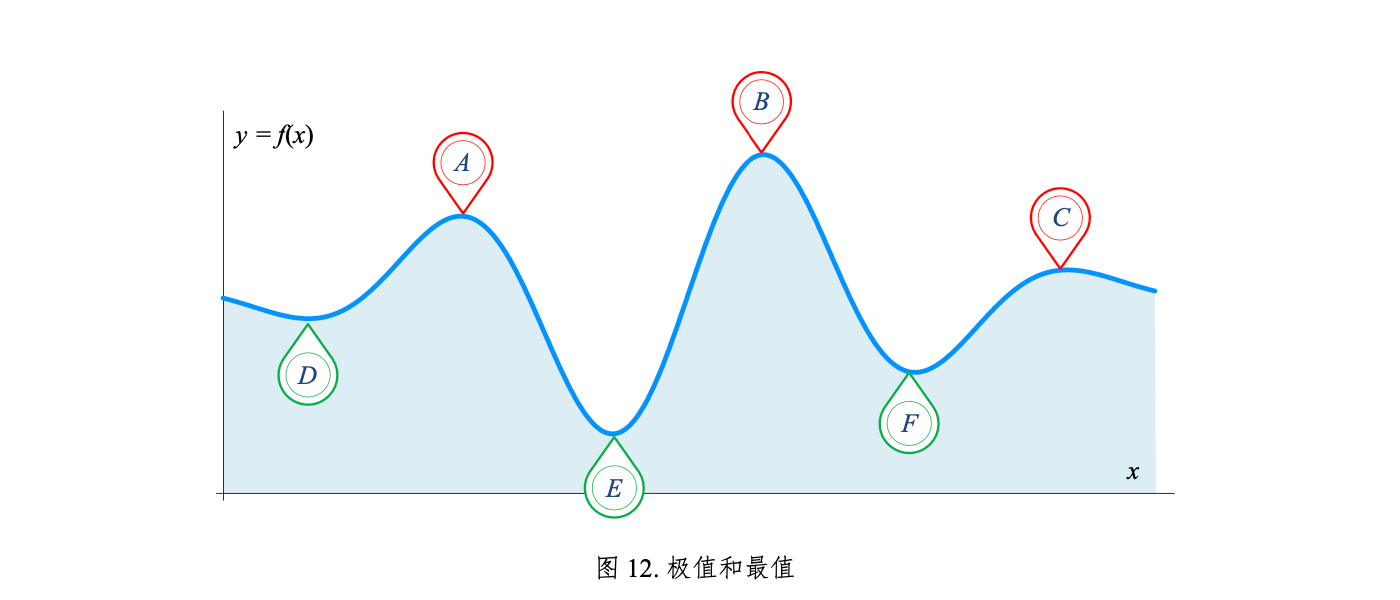
极值

极大值和极小值统称极值 (extrema 或 local extrema)

极大值 (maxima 或 local maxima 或 relative maxima)

极小值 (minima 或 local minima 或 relative minima)

最值

最大值和最小值统称最值 (global extrema)。

最大值 (maximum 或 global maximum 或 absolute maximum)

最小值 (minimum 或 global minimum 或 absolute minimum)

极值是就局部而言，而最值是整体来看。极值是局部的最大或最小值，而最值是整体 的最大或最小值。

©️周期性

f(x+T)= f(x)，其中，T 为周期 (period)，也叫最小正周期。三角函数就是典型的周期函数。

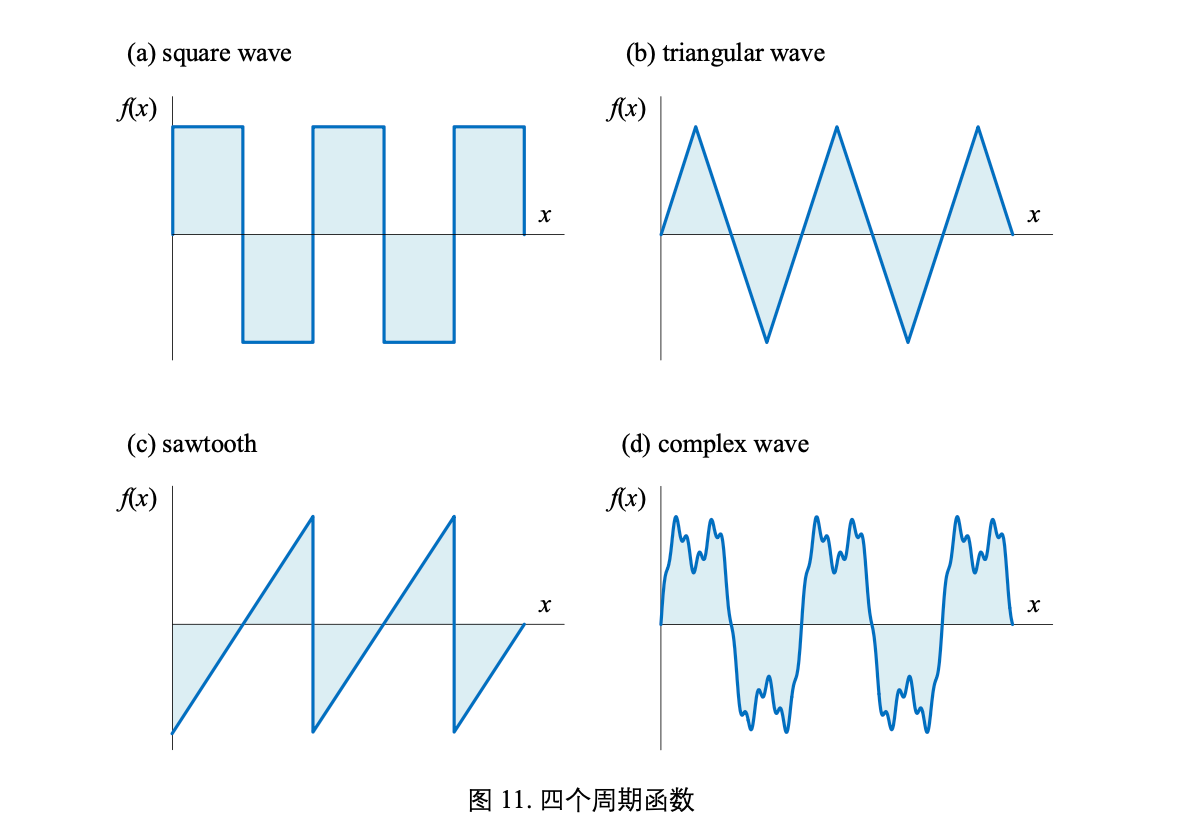
数学和算法

在机器学习中，欧氏距离是最基础的距离度量，每种距离度量都有自己独特的“等距线”。

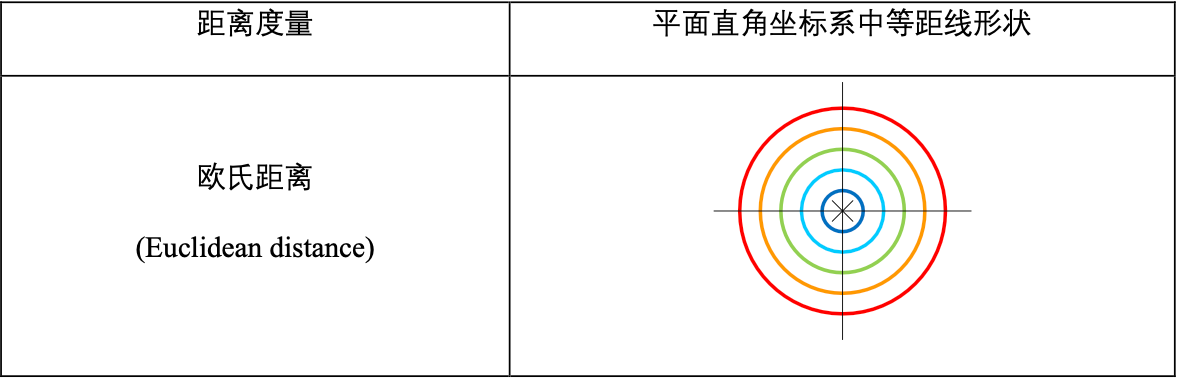
其他5类距离的表现

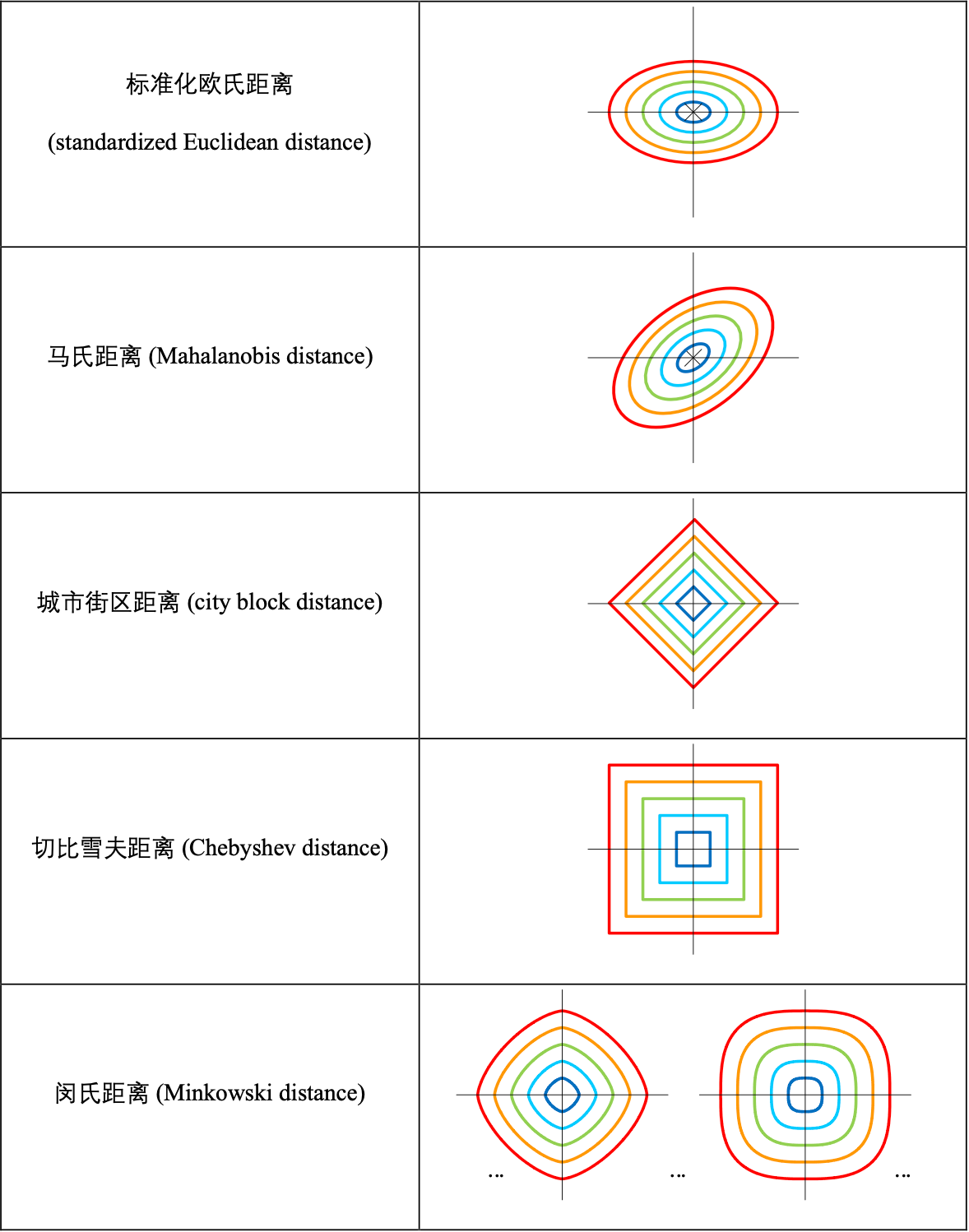
p 和 q 取不同值时，对应超椭圆的形状

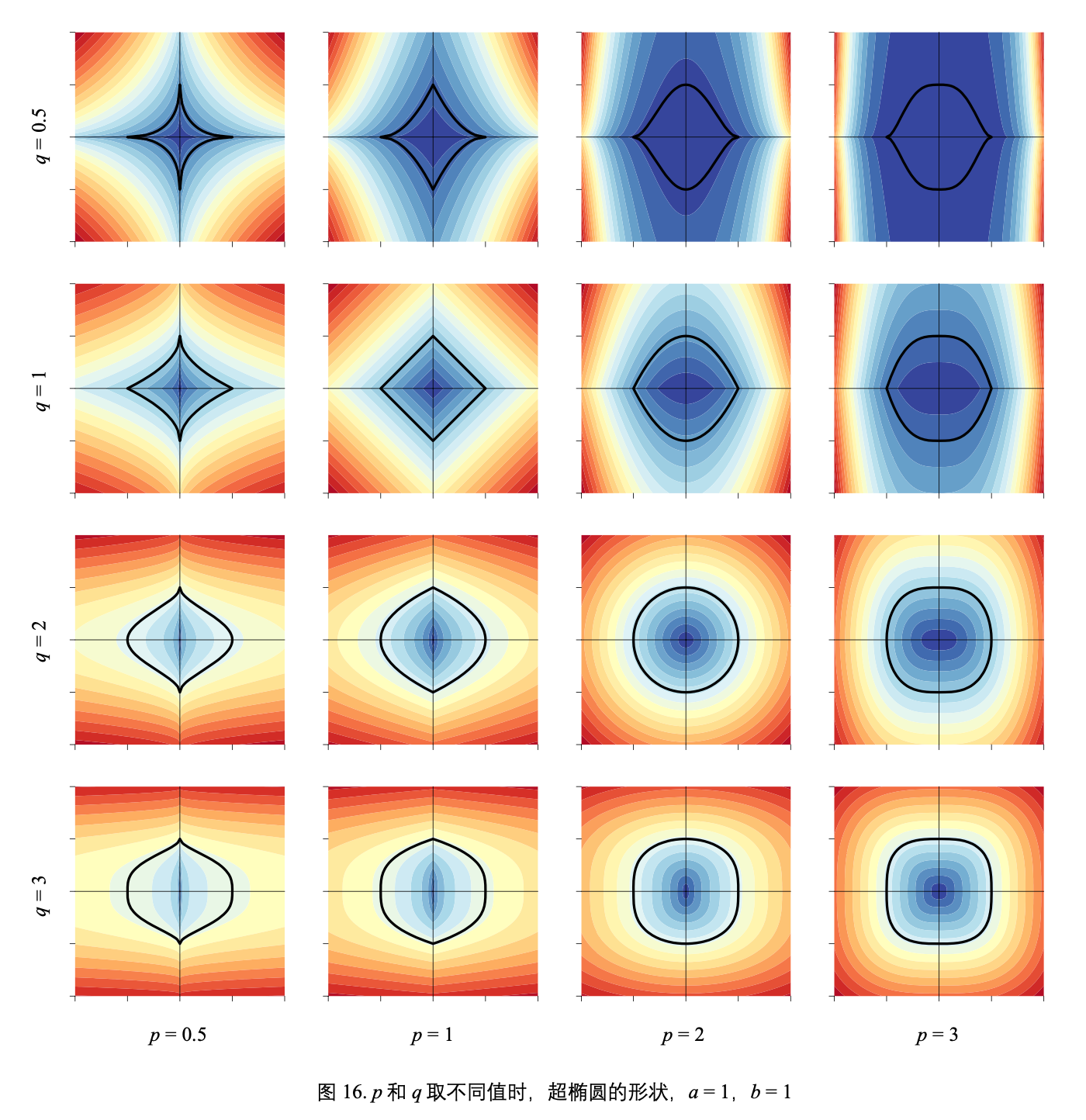
a = 1 和 b = 1，t 和 r 取不同值时，超椭球的形状

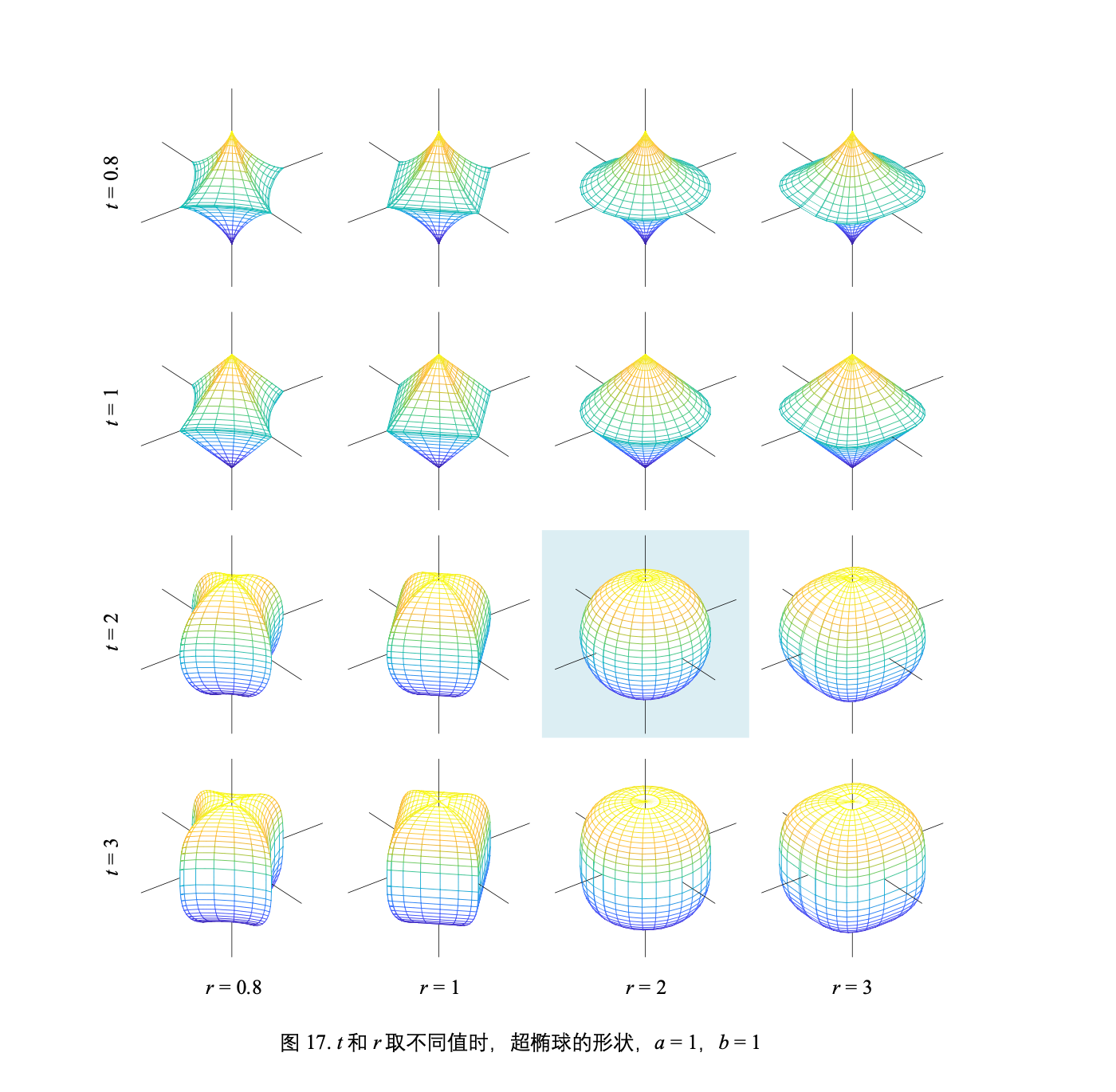
从平面到多元空间

隐函数 (implicit function) 是由隐式方程 (implicit equation) 所隐含定义的函数

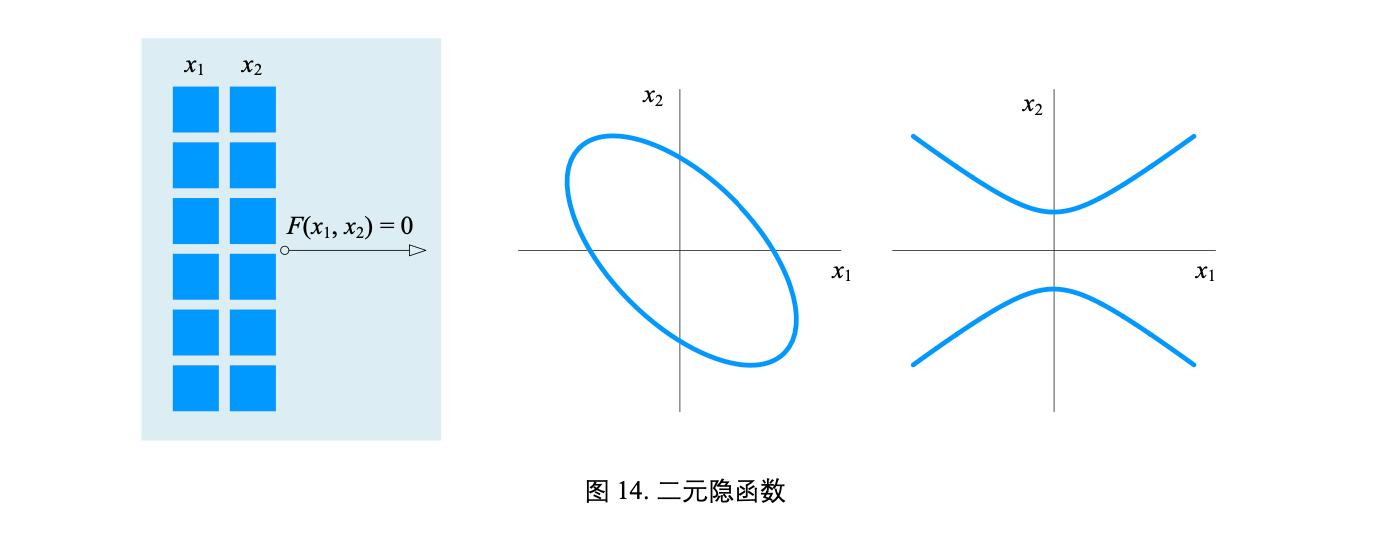
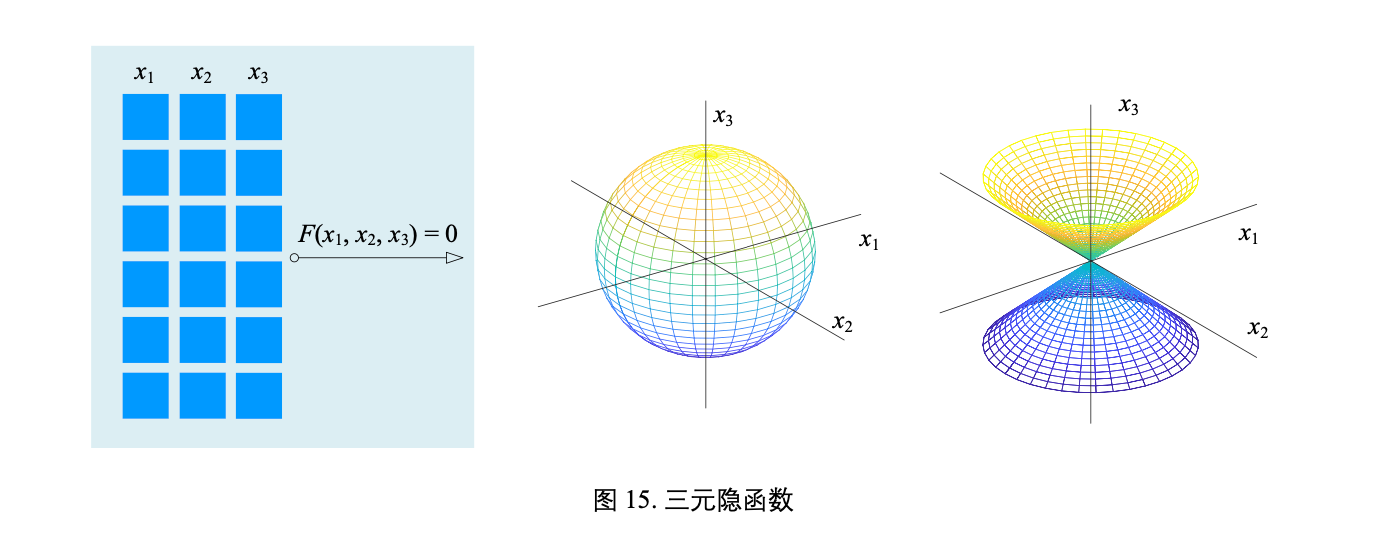
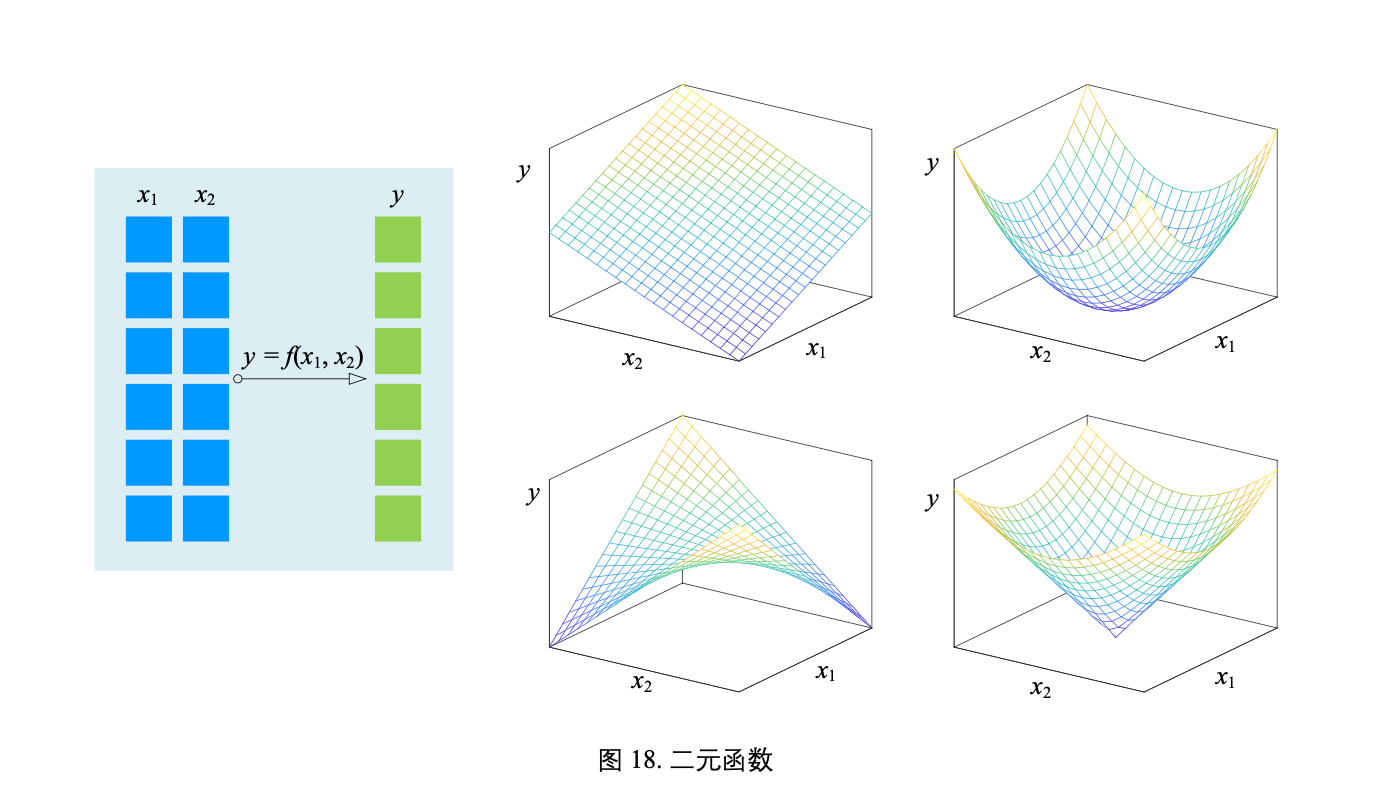
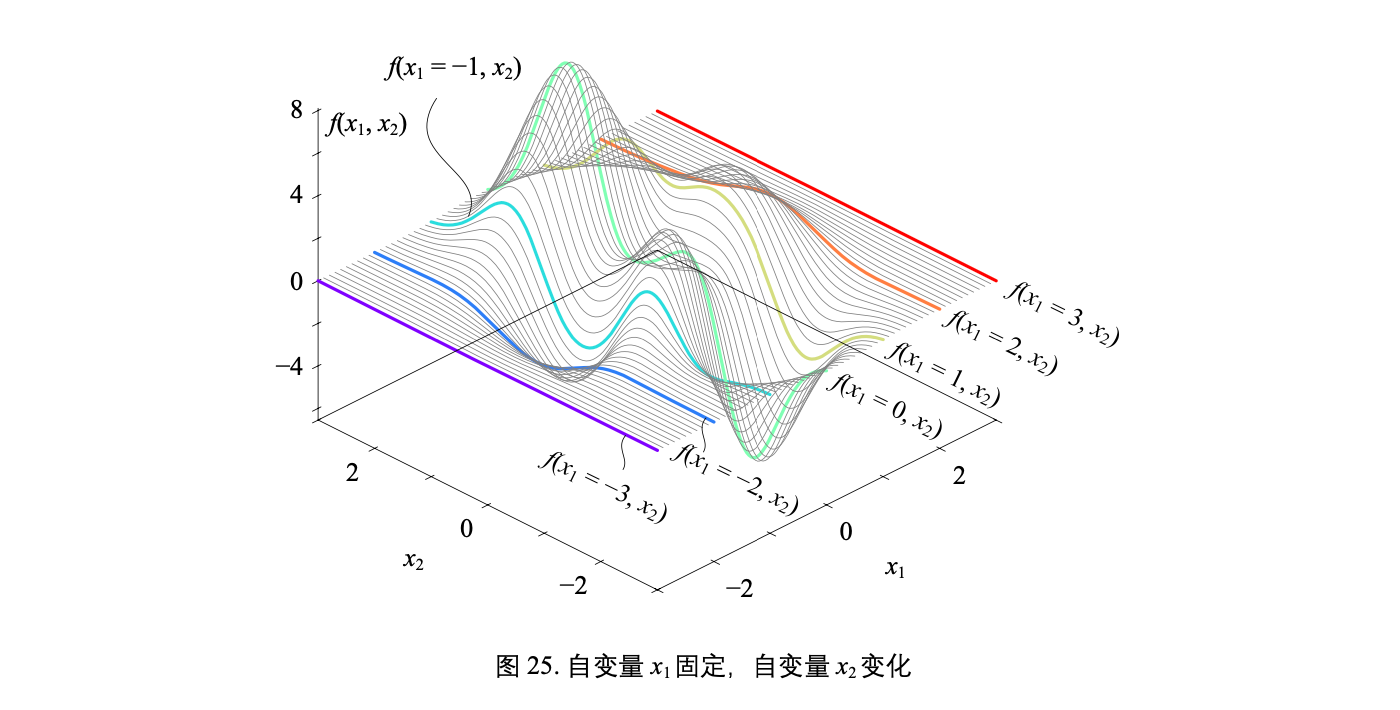
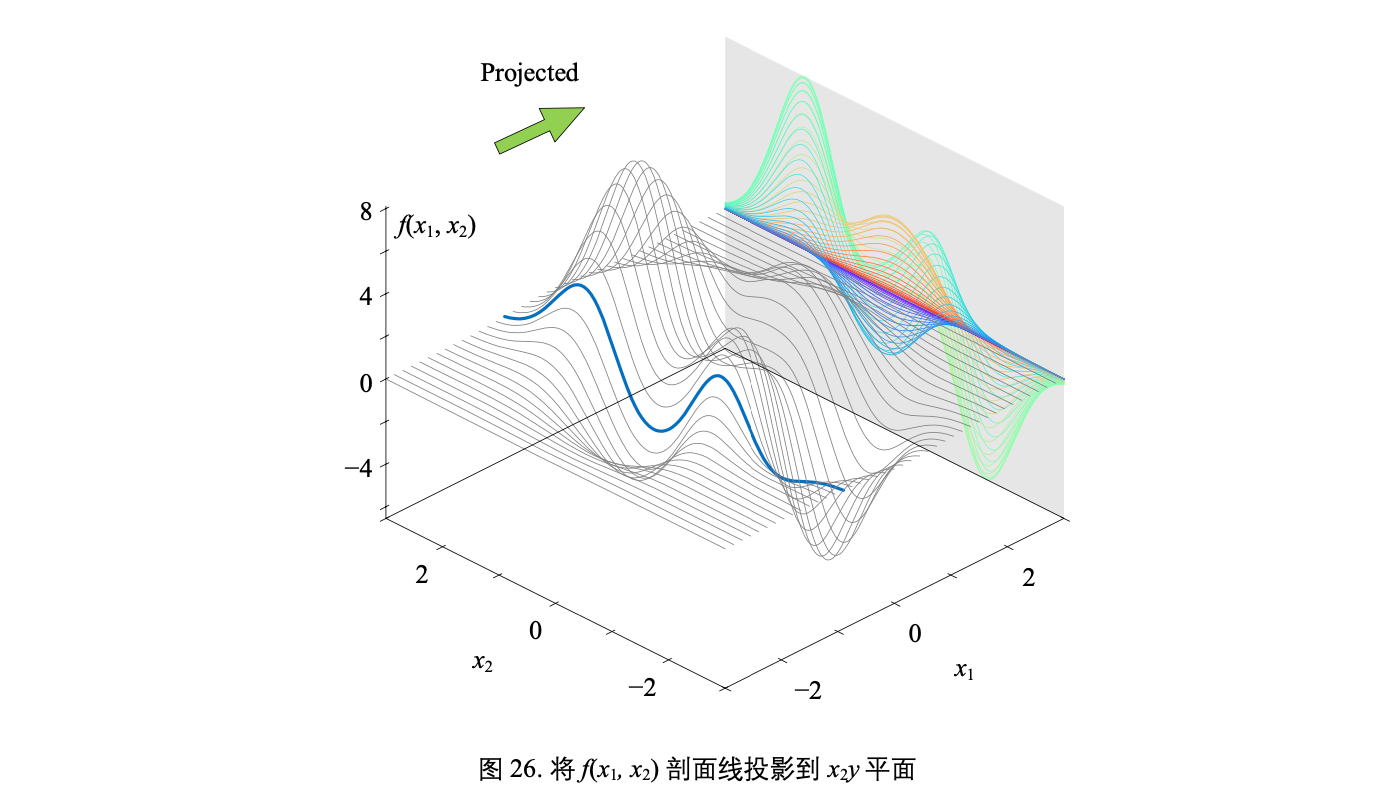
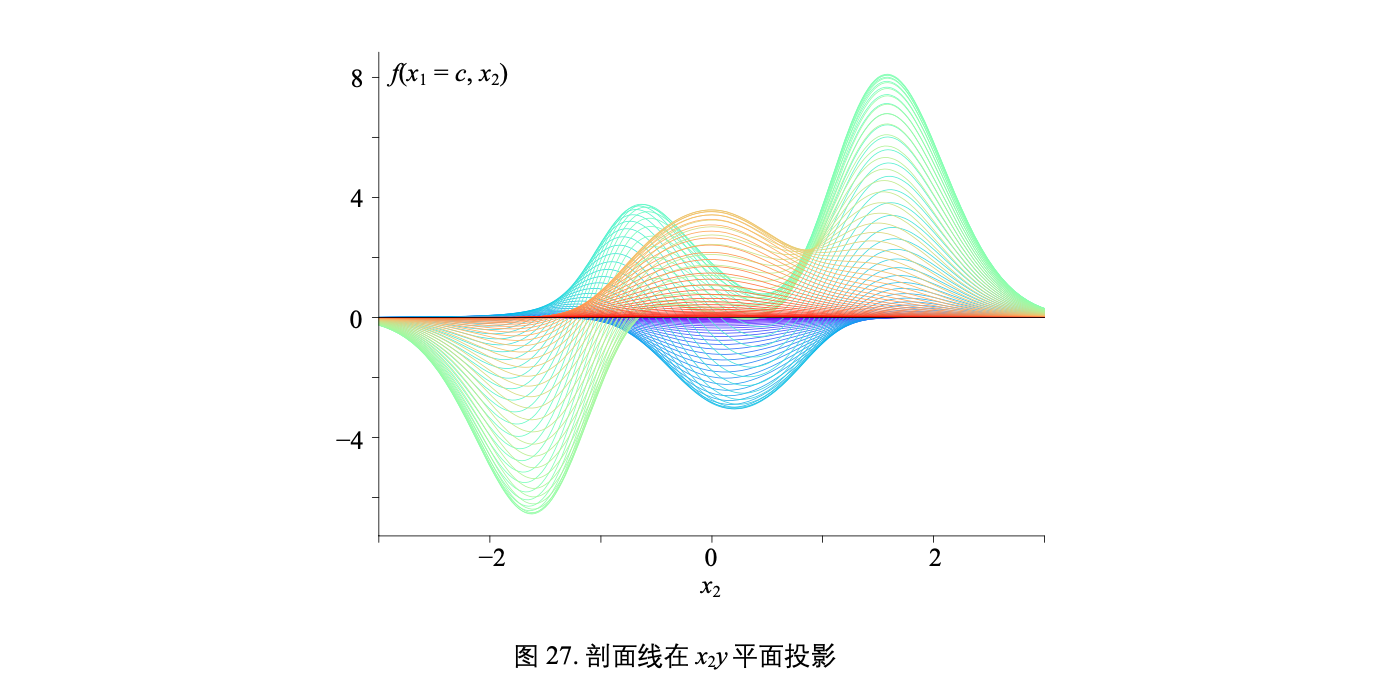
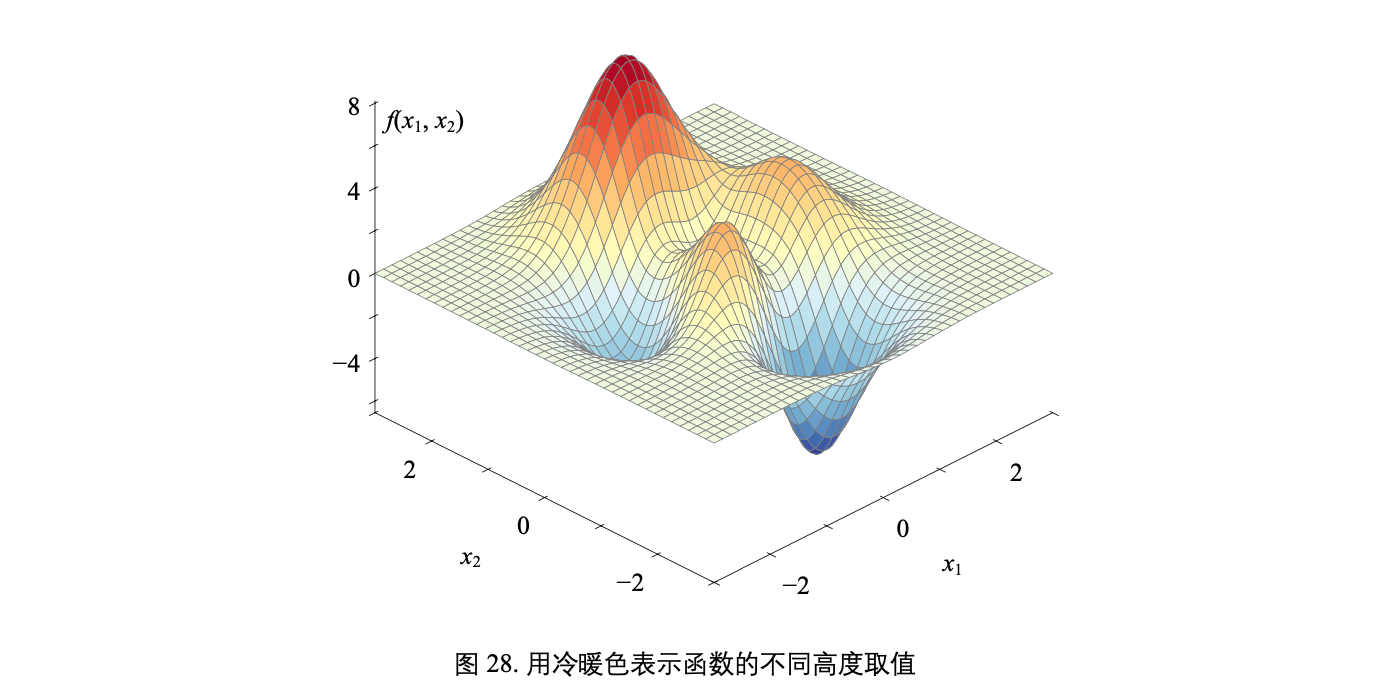
有两个自变量函数叫做二元函数 (bivariate function)，比如 y = f(x1, x2)

有多个自变量函数叫做多元函数 (multivariate function)，比如 y = f(x1, x2, ... xD) 有 D 个自变量。

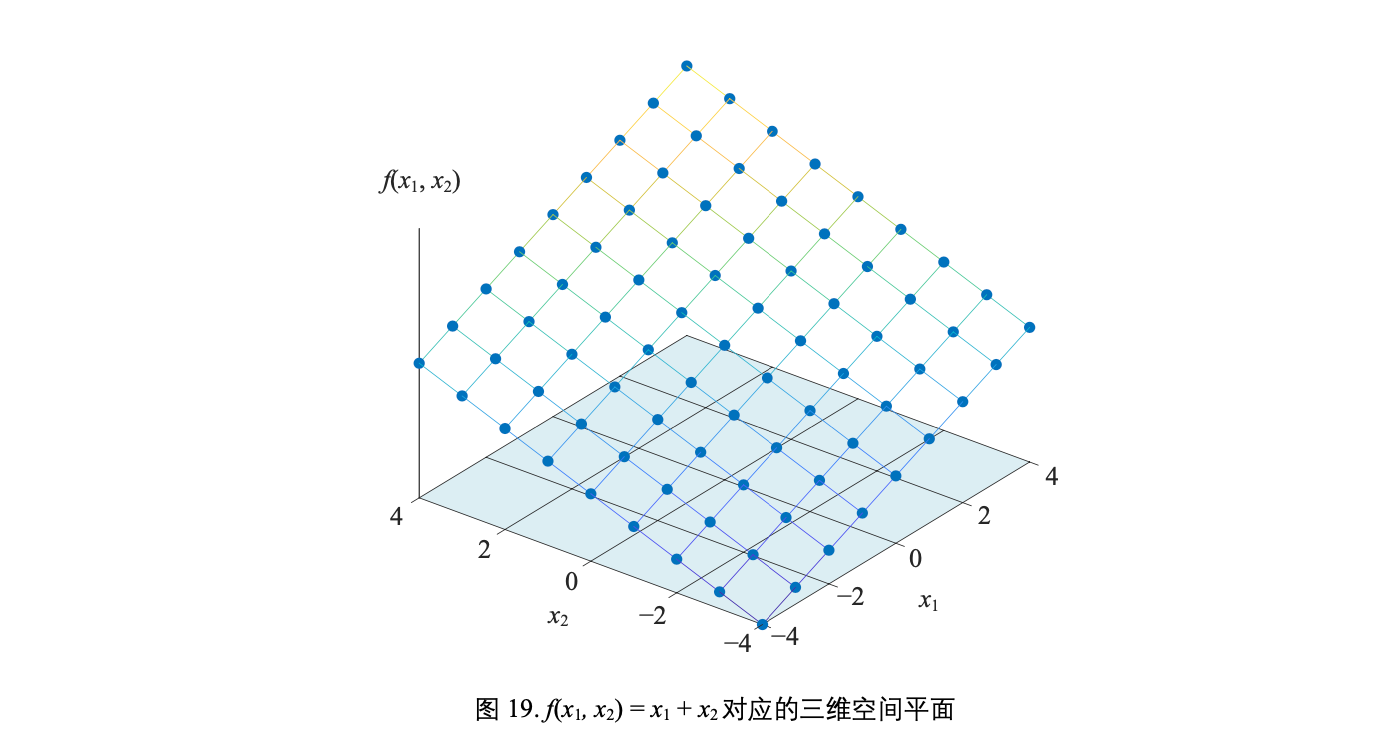
f(x1, x2) = x1 + x2 对应的三维空间平面

一个复杂二元函数 f(x1, x2) 对应的曲面

---

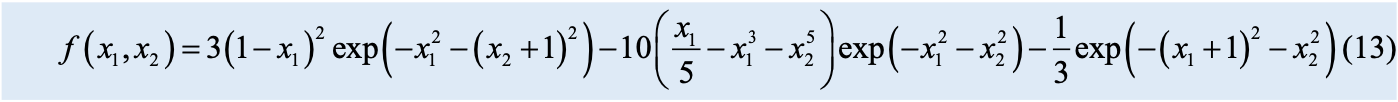
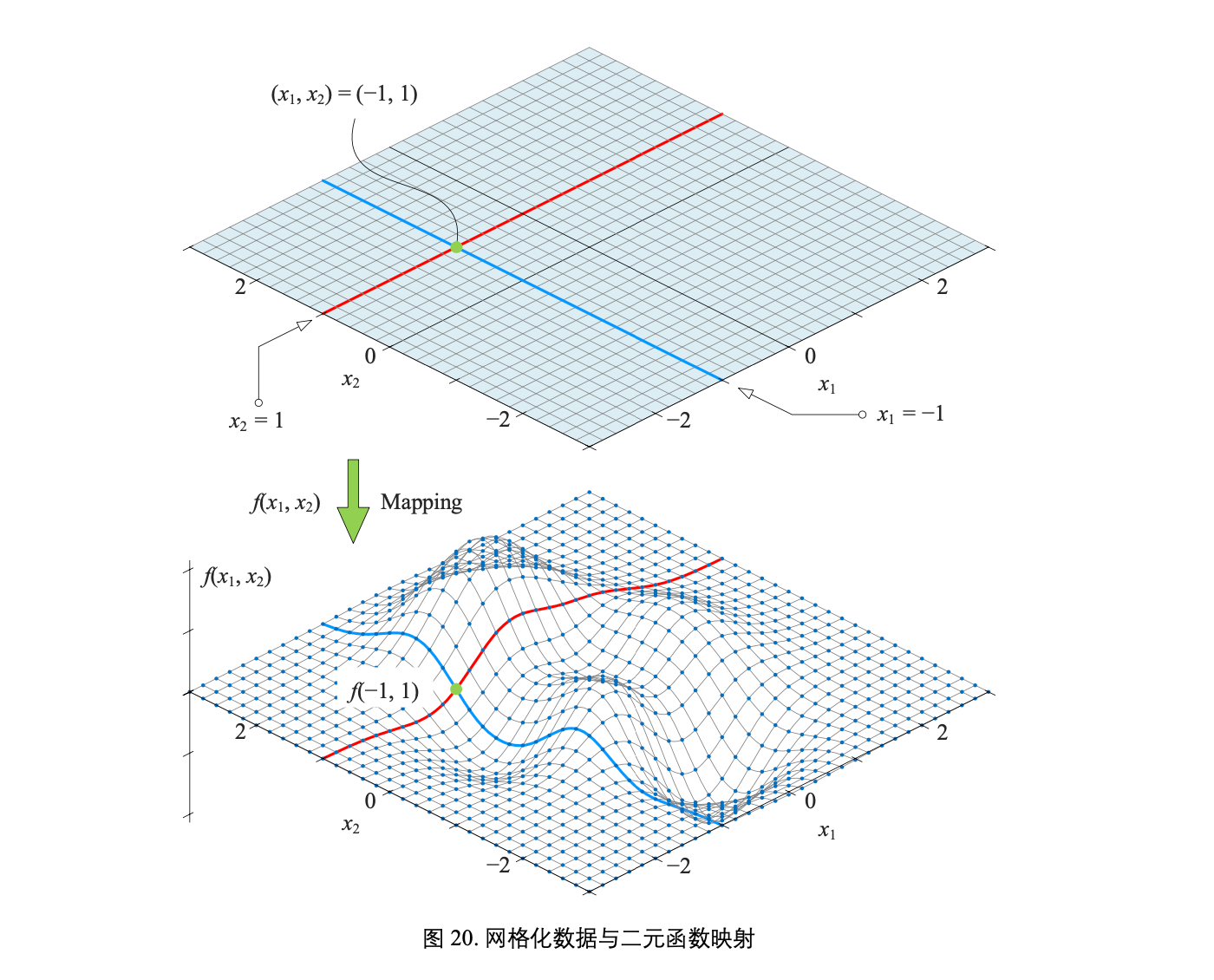
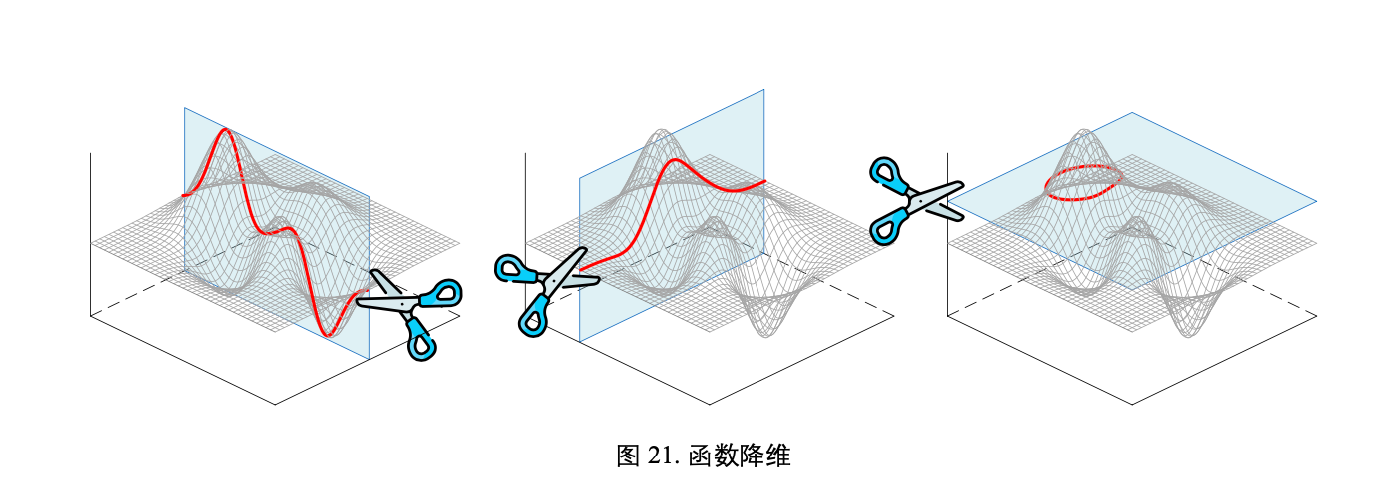
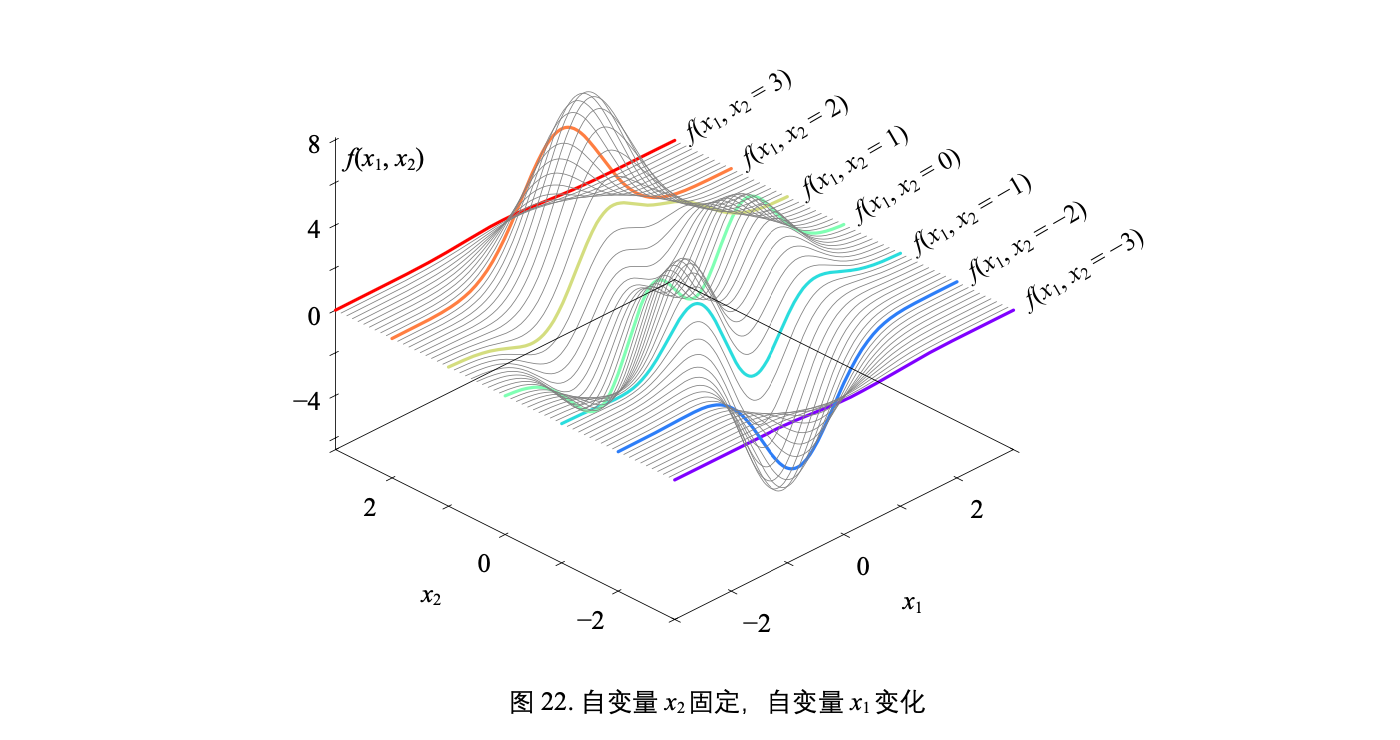
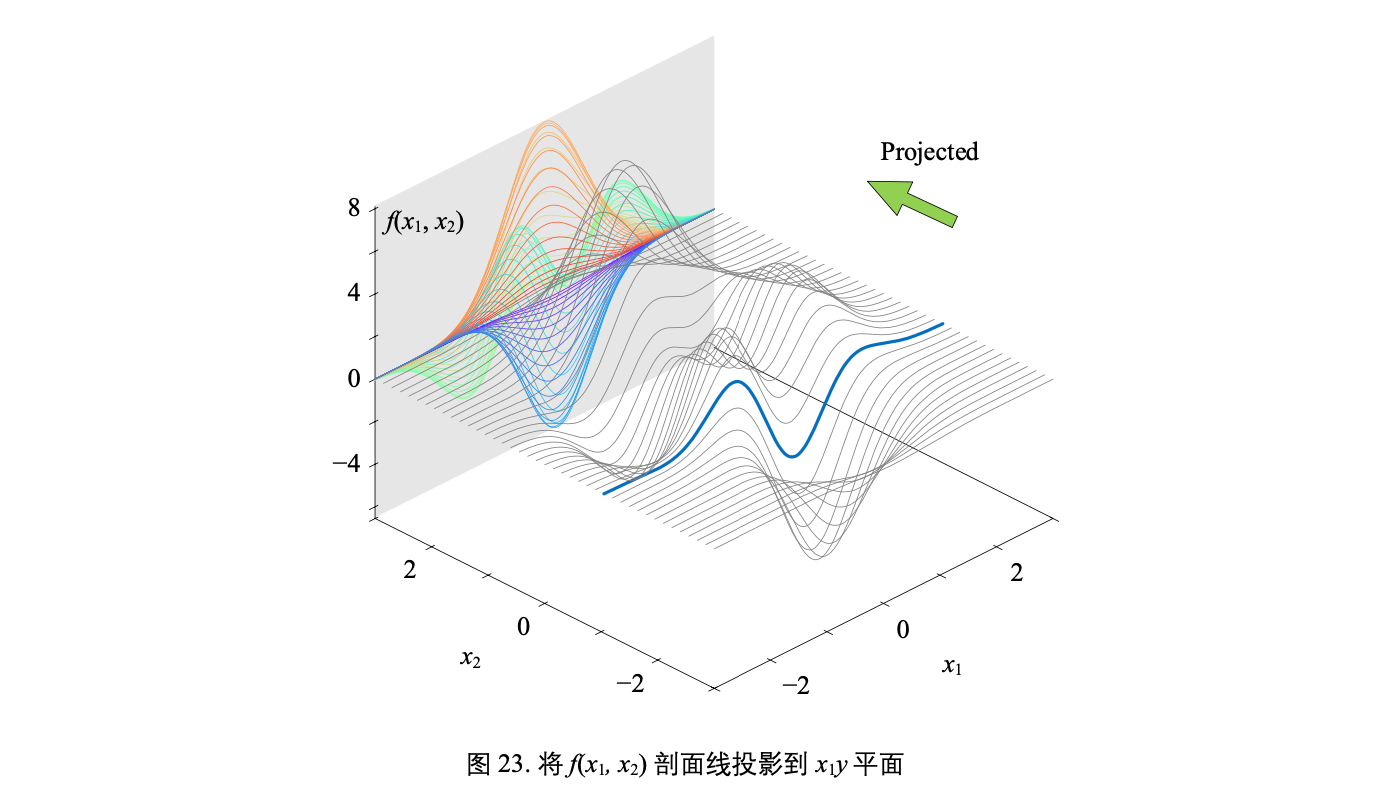
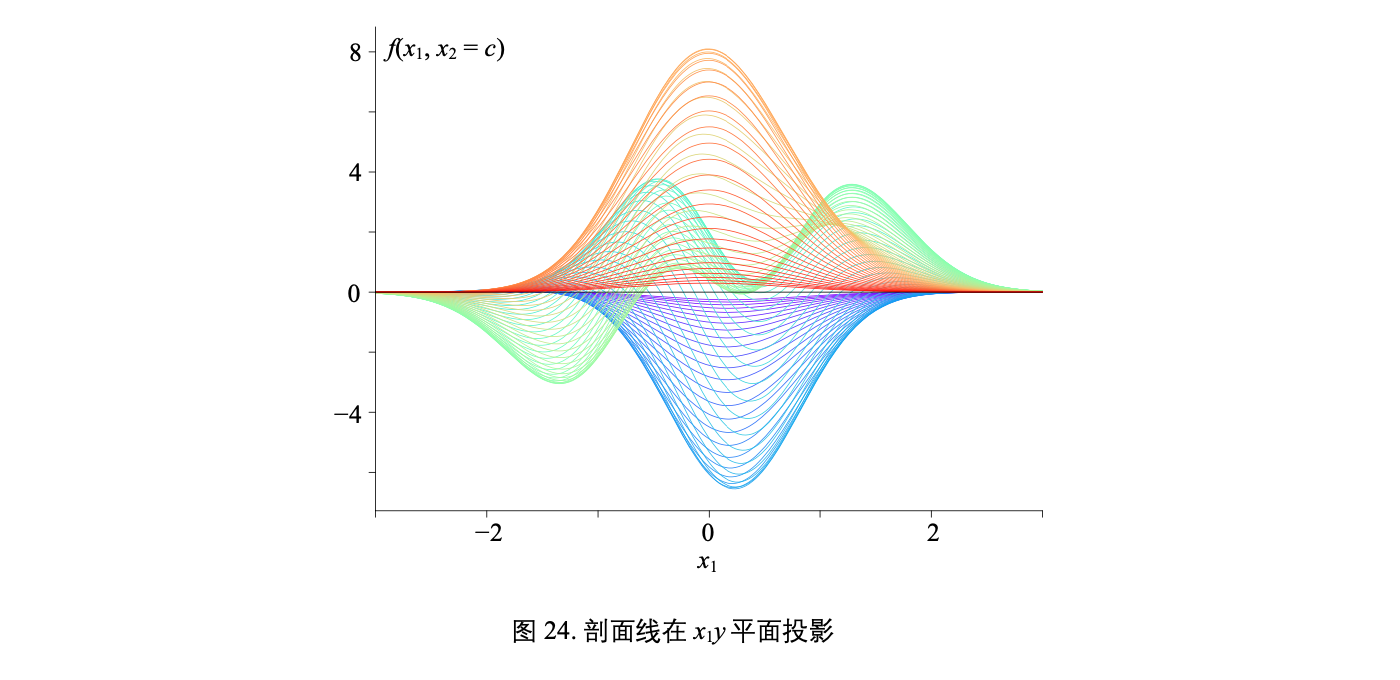
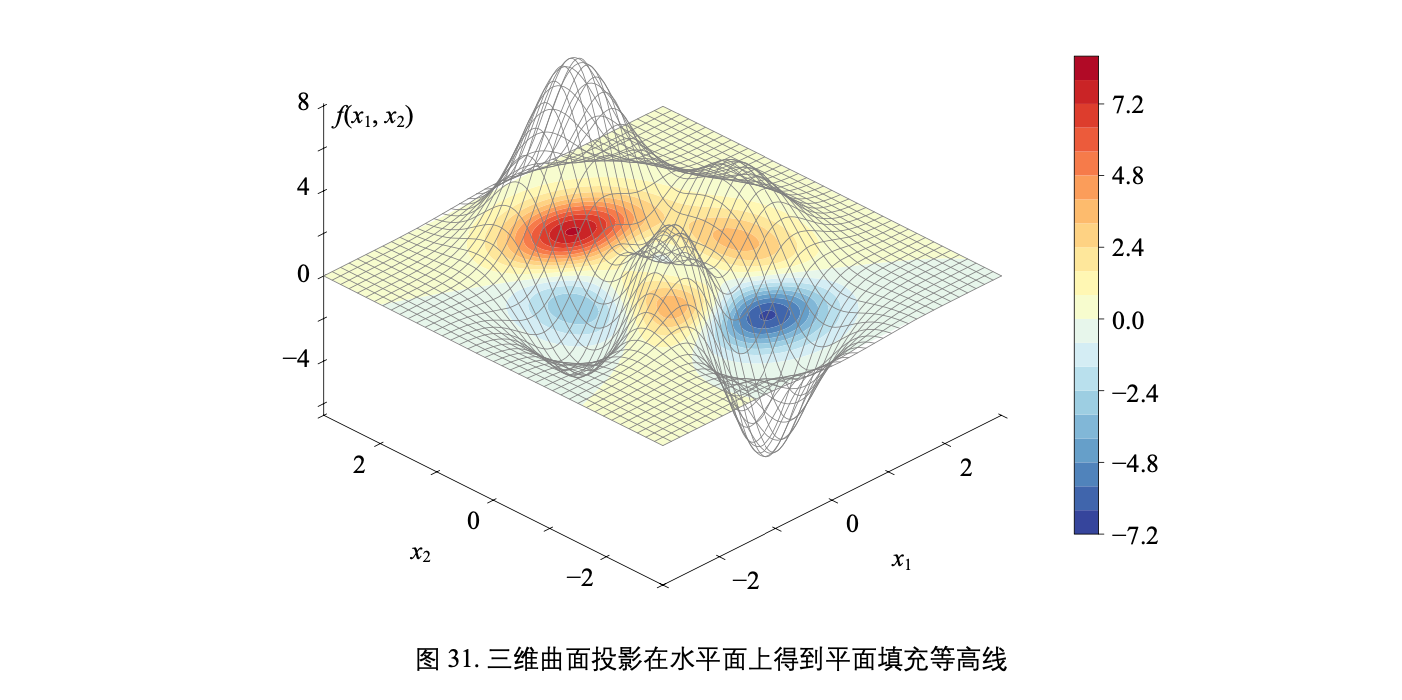
可以引用三体中的一句话：

我们都是阴沟里的虫子，但总还是得有人仰望星空。

如果把数学和图结合在一起，可以很有意思。