Leetcode之DP+滚动数组之Unique Path, Minimum Sum Path

题目：

1.

A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).

How many possible unique paths are there?

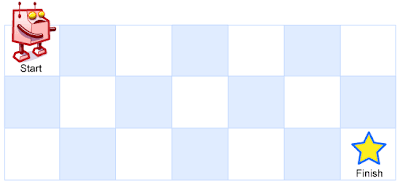
Above is a 3 x 7 grid. How many possible unique paths are there?

Note: m and n will be at most 100.

» Solve this problem

2.

Follow up for "Unique Paths":

Now consider if some obstacles are added to the grids. How many unique paths would there be?

An obstacle and empty space is marked as 1 and 0 respectively in the grid.

For example,

There is one obstacle in the middle of a 3x3 grid as illustrated below.

[
  [0,0,0],
  [0,1,0],
  [0,0,0]
]

The total number of unique paths is 2.

Note: m and n will be at most 100.

» Solve this problem

3.

Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right which minimizes the sum of all numbers along its path.

Note: You can only move either down or right at any point in time.

» Solve this problem

分析：

三道题目如出一辙，分别可以用递归，二维DP，一维DP的解法，先放代码。

代码：

1. Unique Path I

//一维DP法
public class Solution {
    public int uniquePaths(int m, int n) {
        // Start typing your Java solution below
        // DO NOT write main() function
        int[] dp = new int[n];
        dp[0] = 1;
        for(int i=0; i<m; i++)
            for(int j=1; j<n; j++)
                dp[j] = dp[j] + dp[j-1];
        return dp[n-1];
    }
}


//二维DP法
public class Solution {
    public int uniquePaths(int m, int n) {
        // Start typing your Java solution below
        // DO NOT write main() function
        int[][] matrix = new int[m][n];
        for(int i=0; i<m; i++) matrix[i][0] = 1;
        for(int i=0; i<n; i++) matrix[0][i] = 1;
        for(int i=1; i<m; i++)
            for(int j=1; j<n; j++)
                matrix[i][j] = matrix[i-1][j] + matrix[i][j-1];
        return matrix[m-1][n-1];
    }
}




public class Solution {
    public int uniquePaths(int m, int n) {
        // Start typing your Java solution below
        // DO NOT write main() function
        int[][] dp = new int[m][n];
        for(int i=0; i<m; i++){
            dp[i][0] = 1;
            for(int j=0; j<n; j++){
                dp[0][j] = 1;
                if(i>0 && j>0)
                    dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
        
        return dp[m-1][n-1];
    }
}

2. Unique Path II

//一维DP法
public class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int m = obstacleGrid.length;
        int n = obstacleGrid[0].length;
        int[] dp = new int[n+1];
        if(obstacleGrid[0][0] == 0) dp[1] = 1;
        for(int i=0; i<m; i++)
            for(int j=0; j<n; j++)
                dp[j+1] = obstacleGrid[i][j]==1?0:dp[j]+dp[j+1];
        return dp[n];
    }
}

//二维DP法
public class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        // Start typing your Java solution below
        // DO NOT write main() function
        if(obstacleGrid==null || obstacleGrid.length==0 || obstacleGrid[0][0]==1) return 0;
        int m = obstacleGrid.length, n = obstacleGrid[0].length;
        int[][] dp = new int[m][n];
        dp[0][0] = 1;
        for(int i=1; i<m; i++){
            if(obstacleGrid[i][0] == 1) dp[i][0] = 0;
            else dp[i][0] = dp[i-1][0];
        }
        for(int j=1; j<n; j++){
            if(obstacleGrid[0][j] == 1) dp[0][j] = 0;
            else dp[0][j] = dp[0][j-1];
        }
        for(int i=1; i<m; i++){
            for(int j=1; j<n; j++){
                if(obstacleGrid[i][j]==1) dp[i][j] = 0;
                else dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }
}

//递归法
public class Solution {
    public int uniquePaths(int m, int n) {
        // Start typing your Java solution below
        // DO NOT write main() function
        if(m==1 && n==1) return 1;
        if(m==1 || n==1) return 1;
        return uniquePaths(m-1, n) + uniquePaths(m, n-1);
    }
}

3. Minimum Sum Path

//一维DP
public class Solution {
    public int minPathSum(int[][] grid) {
        // Start typing your Java solution below
        // DO NOT write main() function
        int m = grid.length, n = grid[0].length;
        int[] dp = new int[n];
        for(int i=0; i<m; i++)
            for(int j=0; j<n; j++){
                if(i==0 && j==0) dp[0] = grid[0][0];
                else if(i == 0) dp[j] = grid[0][j] + dp[j-1];
                else if(j == 0) dp[j] = grid[i][0] + dp[0];
                else dp[j] = grid[i][j] + Math.min(dp[j], dp[j-1]);
            }
        return dp[n-1];
    }
}

//二维DP
public class Solution {
    public int minPathSum(int[][] grid) {
        // Start typing your Java solution below
        // DO NOT write main() function
        int m = grid.length, n = grid[0].length;
        int[][] dp = new int[m][n];
        dp[0][0] = grid[0][0];
        for(int i=1; i<m; i++) dp[i][0] = grid[i][0] + dp[i-1][0];
        for(int j=1; j<n; j++) dp[0][j] = grid[0][j] + dp[0][j-1];
        for(int i=1; i<m; i++)
            for(int j=1; j<n; j++)
                dp[i][j] = grid[i][j] + Math.min(dp[i-1][j], dp[i][j-1]);
        return dp[m-1][n-1];                
    }
}

小结：

二维数组的DP算法简单明了，从左上到右下的遍历，选择最优元素并带到下层遍历，最后结束遍历，返回最终值，即最优解。

一维数组DP算法可以看做二维，就想n-queen问题中的board[i]=j的思路一样。具体的解释是，在一个二层循环遍历里，当前的dp[j]表示当前的i,j位置，同时又表示(i-1, j)的位置，而dp[j-1]表示(i, j-1)的位置。

这就是滚动数组的核心思路，剩下的东西就是选择最优解的DP算法了，比较简单。

滚动算法比二维DP有效的节省了空间。