【数据结构与算法】第4章树_d(n) internal path length-CSDN博客

本文链接：https://blog.csdn.net/lc250123/article/details/82117215

博客介绍了多种树结构。链表不适用于大量输入数据，树采用第一儿子/下一兄弟表示法实现。介绍了二叉树、二叉查找树、AVL树、伸展树、B树的特性、操作及平衡调整方法。还提及B树在磁盘数据存储中的应用，最后说明了树在标准库set和map容器中的应用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Table of Contents

对于大量的输入数据，链表的线性访问时间太长，不宜使用。

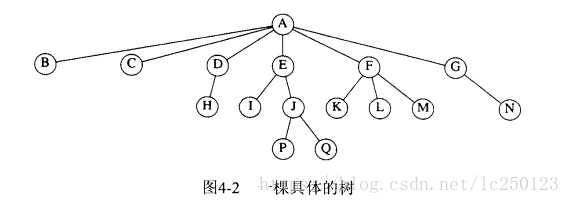
树的实现

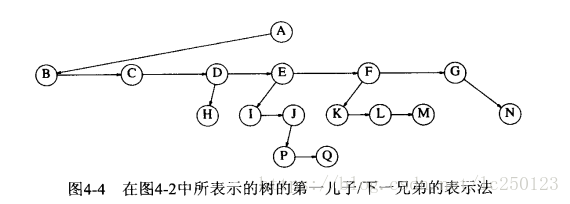
由于树的每个结点的儿子数可能变化很大并且事先不知道，因此在数据结构中建立到各儿子结点的直接链接是不可行的，因为这会产生太多浪费的空间。最好的办法是使用：第一儿子/下一兄弟表示法。

        struct TreeNode
        {
            Object        element;
            TreeNode     *firstChild;
            TreeNode     *nextSibling;
        }

结点的所有儿子结点都放在 firstChild 链表中，兄弟结点在 nextSibling 链表中。

二叉树

因为一个二叉树结点最多有两个儿子，所以可以直接链接到它们。实现如下

        struct BinaryNode
        {
            Object      element;      // The data in the node
            BinaryNode *left;         // Left child
            BinaryNode *right;        // Right child
        };

具有 N 个结点的二叉树，都将需要 N + 1 个 NULL 链。

二叉树分三种遍历：前根、中根、后根遍历。

查找树 ADT -- 二叉查找树

二叉树的一个重要应用是它们在查找中的应用。

二叉查找树的性质是：对于树中的每个结点 X，它的左子树中所有项的值小于 X 中的项，而它的右子树中所有项的值都大于 X 中的项。

下面的代码中 Comparable 指的是具有比较功能的，查找是基于 “<” 操作符的，所以必须在 Comparable 中进行定义该操作符。

#ifndef BINARYSEARCHTREE_H
#define BINARYSEARCHTREE_H

template <typename Comparable>
class BinarySearchTree
{
public:
    BinarySearchTree( ):root(nullptr){}
    BinarySearchTree( const BinarySearchTree & rhs );
    ~BinarySearchTree( )
        { makeEmpty(); }

    const Comparable & findMin( ) const
        { return findMin(root)->element; }
    const Comparable & findMax( ) const
        { return findMax(root)->element; }
    bool contains( const Comparable & x ) const
        { return contains(x, root); }
    bool isEmpty( ) const
    {
        if( root == nullptr )
            return true;
        else
            return false;
    }
    void printTree( ) const
        { printTree(root); }

    void makeEmpty( )
        { makeEmpty(root); }
    void insert( const Comparable & x )
        { insert(x, root); }
    void remove( const Comparable & x )
        { remove(x, root); }

    const BinarySearchTree & operator=( const BinarySearchTree & rhs )
    {
        if( this != &rhs )
        {
            makeEmpty();
            root = clone(rhs.root);
        }
        return *this;
    }

private:
    struct BinaryNode
    {
       Comparable element;
       BinaryNode *left;
       BinaryNode *right;

       BinaryNode( const Comparable & theElement, BinaryNode *lt, BinaryNode *rt )
         : element( theElement ), left( lt ), right( rt ) { }
    };

    BinaryNode *root;   // 根节点

    void insert( const Comparable & x, BinaryNode * & t )
    {
        if( t == nullptr ){
            // 如果树中不存在该结点，最终会将树的一个空节点指向这个新节点
            t = new BinaryNode(x, nullptr, nullptr);
        }else if ( x < t->element ) {
            insert( x, t->left );
        }else if ( t->element < x) {
            insert( x, t->right );
        }else {
            ;               // 树中已存在这样的结点，do-nothing
        }
    }
    void remove( const Comparable & x, BinaryNode * & t )
    {
        if( t == nullptr )
            return;
        if( x < t->element )
            remove(x, t->left);
        else if ( t->element < x ) {
            remove(x, t->right);
        }else if ( t->left != nullptr && t->right != nullptr) {
            t->element = findMin(t->right)->element;
            remove(t->element, t->right);
        }else {
            BinaryNode *oldNode = t;
            t = (t->left != nullptr) ? t->left : t->right;
            delete oldNode;
        }
    }
    BinaryNode * findMin( BinaryNode *t ) const
    {
        if( t == nullptr )
            return nullptr;
        if( t->left == nullptr )
            return t;

        return findMin(t->left);
    }
    BinaryNode * findMax( BinaryNode *t ) const
    {
        if( t == nullptr)
            return nullptr;
        if( t->right == nullptr )
            return t;

        return findMax(t->right);
    }
    bool contains( const Comparable & x, BinaryNode *t ) const
    {
        if( t == nullptr )
            return false;
        else if (x < t->element) {
            return contains(x, t->left);
        }else if (t->element < x) {
            return contains(x, t->right);
        }else {
            return true;  // 匹配
        }
    }
    void makeEmpty( BinaryNode * & t )
    {
        if( t != nullptr)
        {
            makeEmpty(t->left);
            makeEmpty(t->right);
            delete t;
        }
        t = nullptr;
    }
    void printTree( AvlNode *t, void *arg ) const   // 后根遍历打印
    {
        if( t == nullptr )
            return;
        if( t->left )
            printTree(t->left, arg);
        if( t->right )
            printTree(t->right, arg);

        printf((char *)arg, t->element);
    }
    BinaryNode * clone( BinaryNode *t ) const
    {
        if( t == nullptr )
            return nullptr;

        return new BinaryNode(t->element, clone(t->left), clone(t->right));
    }
};


#endif // BINARYSEARCHTREE_H

上面是 BinarySearchTree 的实现代码。

一棵树的所有结点的深度和称为 内部路径长（internal path length），记为 D(N)。根结点的深度为 0。

可以推得：D(N) = O(NlogN)。所以任意结点预期的深度为 O(logN)。通常是以 2 为底的 log(N) 稍多一些。

上面的代码中，remove 操作始终使用右侧子树中的最小点代替被删除的操作，多次的 insert / remove 操作后二叉树明显的不平衡状态。

AVL 树

AVL 树是带有平衡条件的二叉查找树。一颗 AVL 树是每个结点的左子树和右子树的高度最多差 1 的二叉查找树（空树的高度定义为 -1）。

对 AVL 树，插入和删除操作会引起它的不平衡。

引起不平衡的插入操作有以下四种情景：

（1）对 A 结点的左儿子的左子树进行一次插入
（2）对 A 结点的左儿子的右子树进行一次插入
（3）对 A 结点的右儿子的左子树进行一次插入
（4）对 A 结点的左儿子的右子树进行一次插入

其中（1）和（4）成镜像对称，调整平衡需要 “单旋转” 操作，（2）和（3）成镜像对称，调整平衡需要 “双旋转” 操作。

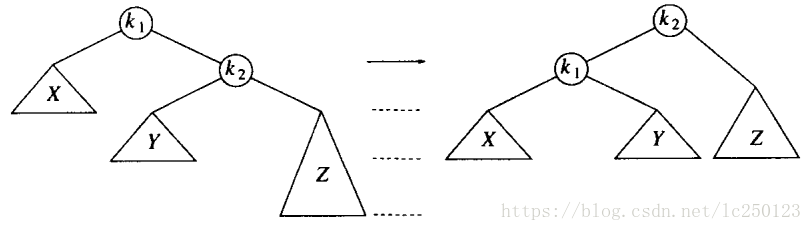
单旋转：

对应情景（1）：对 k2 结点的左儿子的左子树进行一次插入

对应情景（4）：对 k1 结点的左儿子的右子树进行一次插入

双旋转：

对于如下的情形，单旋转并不能解决：

因为 Y 过深，所以不管怎么单旋转都无法达到平衡。

对应情景（2）：对 k3 结点的左儿子的右子树进行一次插入

对应情景（3）：对 k1 结点的右儿子的左子树进行一次插入

下面的代码中 Comparable 指的是具有比较功能的，查找是基于 “<” 操作符的，所以必须在 Comparable 中进行定义该操作符。

#ifndef AVLTREE_H
#define AVLTREE_H

#define max(a, b) ((a)>(b)?(a):(b))

template <typename Comparable>
class AvlTree
{
public:
    AvlTree( ):root(nullptr){}
    AvlTree( const AvlTree & rhs );
    ~AvlTree( )
        { makeEmpty(); }

    const Comparable & findMin( ) const
        { return findMin(root)->element; }
    const Comparable & findMax( ) const
        { return findMax(root)->element; }
    bool contains( const Comparable & x ) const
        { return contains(x, root); }
    bool isEmpty( ) const
    {
        if( root == nullptr )
            return true;
        else
            return false;
    }
    void printTree( void *arg ) const
        { printTree(root, arg); }

    void makeEmpty( )
        { makeEmpty(root); }
    void insert( const Comparable & x )
        { insert(x, root); }
    void remove( const Comparable & x )
        { remove(x, root); }

    const AvlTree & operator=( const AvlTree & rhs )
    {
        if( this != &rhs )
        {
            makeEmpty();
            root = clone(rhs.root);
        }
        return *this;
    }

private:
    struct AvlNode
    {
       Comparable element;
       AvlNode *left;
       AvlNode *right;
       int height;

       AvlNode( const Comparable & theElement, AvlNode *lt, AvlNode *rt, int h = 0 )
         : element( theElement ), left( lt ), right( rt ), height( h ) { }
    };

    AvlNode *root;   // 根节点

    // 获得结点的高度
    int height( AvlNode *t ) const
    {
        return t == nullptr ? -1 : t->height;
    }

    /*
     *              k2              k1
     *             /  \            /  \
     *            k1   A    -->  k3    k2
     *           /  \            |    /  \
     *          k3   B           O   B    A
     *          |
     *          O
     */
    void rotateWithLeftChild(AvlNode * & k2)
    {
        AvlNode *k1 = k2->left;
        k2->left = k1->right;
        k1->right = k2;
        k2->height = max(height(k2->left), height(k2->right)) + 1;
        k1->height = max(height(k1->left), k2->height) + 1;

        //此时该部分的根节点变成 k1，由于是引用，直接赋值就可改变
        //原来 k2 的父节点指向孩子的指针为 k1
        k2 = k1;
    }

    /*
     *              k1              k2
     *             /  \            /  \
     *            A   k2    -->   k1   K3
     *               /  \        /  \   |
     *              B   K3      A    B  O
     *                   |
     *                   O
     */
    void rotateWithRightChild(AvlNode * & k1)
    {
        AvlNode *k2 = k1->right;
        k1->right = k2->left;
        k2->left = k1;
        k1->height = max(height(k1->left), height(k1->right)) + 1;
        k2->height = max(height(k2->right), k1->height) + 1;

        k1 = k2;
    }

    /*
    *        k3              k3         k3            k2          k2
    *       /  \            /  \       /  \          /  \        /  \
    *      k1   B    -->   k2   B 或  k2   B  -->   k1   k3  或 k1   k3
    *     /  \            /  \       /             /    / \    /  \   \
    *    A   k2          k1   O     k1            A    O   B  A    O   B
    *         |         /          /  \
    *         O        A          A    O
    */
    void doubleWithLeftChild(AvlNode * & k3)
    {
        rotateWithRightChild(k3->left);
        rotateWithLeftChild(k3);
    }

    /*
    *        k3              k3           k3             k2          k2
    *       /  \            /  \         /  \           /  \        /  \
    *      A    k1    -->  A   k2    或  A   k2  -->   k3   k1  或 k3   k1
    *          /  \           /  \            \       / \    \    /    /  \
    *         k2   B         O   k1           k1     A   O    B  A    O    B
    *         |                    \         /  \
    *         O                     B       O    B
    */
    void doubleWithRightChild(AvlNode * & k3)
    {
        rotateWithLeftChild(k3->right);
        rotateWithRightChild(k3);
    }

    void rebalance(AvlNode * & t)
    {
        if(t){
            int diff = height(t->left) - height(t->right);
            if(diff == 2)
            {
                if(height(t->left->left) - height(t->right) == 1)
                    rotateWithLeftChild(t);
                else
                    doubleWithLeftChild(t);
            }

            if(diff == -2)
            {
                if(height(t->right->right) - height(t->left) == 1)
                    rotateWithRightChild(t);
                else
                    doubleWithRightChild(t);
            }
        }
    }

    void insert( const Comparable & x, AvlNode * & t )
    {
        if( t == nullptr ){
            // 如果树中不存在该结点，最终会将树的一个空节点指向这个新节点
            t = new AvlNode(x, nullptr, nullptr);
        }else if ( x < t->element ) {
            insert( x, t->left );
            rebalance(t);
        }else if ( t->element < x) {
            insert( x, t->right );
            rebalance(t);
        }else {
            ;               // 树中已存在这样的结点，do-nothing
        }

        t->height = max(height(t->left), height(t->right)) + 1;
    }

    void remove( const Comparable & x, AvlNode * & t )
    {
        if( t == nullptr )
            return;
        if( x < t->element ){
            remove(x, t->left);
            rebalance(t);
        }else if ( t->element < x ) {
            remove(x, t->right);
            rebalance(t);
        }else if ( t->left != nullptr && t->right != nullptr) {
            t->element = findMin(t->right)->element;
            remove(t->element, t->right);
            rebalance(t);
        }else {
            AvlNode *oldNode = t;
            t = (t->left != nullptr) ? t->left : t->right;
            delete oldNode;
        }

        if(t != nullptr)
            t->height = max(height(t->left), height(t->right)) + 1;
    }

    AvlNode * findMin( AvlNode *t ) const
    {
        if( t == nullptr )
            return nullptr;
        if( t->left == nullptr )
            return t;

        return findMin(t->left);
    }
    AvlNode * findMax( AvlNode *t ) const
    {
        if( t == nullptr)
            return nullptr;
        if( t->right == nullptr )
            return t;

        return findMax(t->right);
    }
    bool contains( const Comparable & x, AvlNode *t ) const
    {
        if( t == nullptr )
            return false;
        else if (x < t->element) {
            return contains(x, t->left);
        }else if (t->element < x) {
            return contains(x, t->right);
        }else {
            return true;  // 匹配
        }
    }
    void makeEmpty( AvlNode * & t )
    {
        if( t != nullptr)
        {
            makeEmpty(t->left);
            makeEmpty(t->right);
            delete t;
        }
        t = nullptr;
    }
    void printTree( AvlNode *t, void *arg ) const   // 后根遍历打印
    {
        if( t == nullptr )
            return;
        if( t->left )
            printTree(t->left, arg);
        if( t->right )
            printTree(t->right, arg);

        printf((char *)arg, t->element);
    }
    AvlNode * clone( AvlNode *t ) const
    {
        if( t == nullptr )
            return nullptr;

        return new AvlNode(t->element, clone(t->left), clone(t->right), t->height);
    }
};

/*
 * 只要你碰到*&，就应该想到**。也就是说这个函数修改或可能修改调用者的指针，
 * 而调用者像普通变量一样传递这个指针，不使用地址操作符&。
 */
#endif // AVLTREE_H

测试程序：

int main(int argc, char *argv[])
{
    AvlTree<int> avlTree;
    avlTree.insert(20);
    avlTree.insert(30);
    avlTree.insert(10);
    avlTree.insert(22);
    avlTree.insert(40);
    avlTree.insert(50);
    avlTree.insert(44);
    avlTree.insert(55);
    avlTree.insert(12);
    avlTree.insert(3);

    char buf[5] = " %d ";
    avlTree.printTree((void*)buf);

    avlTree.remove(10);
    avlTree.remove(30);
    avlTree.printTree((void*)buf);

    return 0;
}

输出：3 12 10 22 20 40 55 50 44 30

3 12 22 20 44 55 50 40

伸展树

具有这样特性的树叫伸展树：它保证从空树开始，任意连续 M 次对树的操作最多花费 O(MlogN) 时间。如果任意特定操作可以有最坏时间界 O(N)，而我们仍然要求一个 O(logN) 的摊还时间界，那么很清楚，只要有一个结点被访问，它就必须被移动。

因为在许多应用中当一个结点被访问时，它就很可能不久再被访问。而且伸展树还不要求保留高度或平衡信息，因此可以在某种程度上节省空间并简化代码。所以伸展树很有应用场景。

用伸展的方法移动被访问的结点，分以下两种情形：

之字形：

一字形：

对结点 X 的访问会引起右边的结果。

伸展树有几种变体，我们以后讨论。

B 树

考虑这样的情况，有许多数据，内存装不下，那么就意味着必须把数据结构放到磁盘上。而磁盘的的访问时间一般都比较长，拿7200 转/min 的磁盘来说，1 转占用 1/120s，即 8.3ms，平均认为转到一般发现要寻找的信息，即 4.1ms，加上平均寻道时间，一般的访问时间会在 12ms 左右。如果数据存储在硬盘上，以前面的数据结构来说，也就 AVL 树效率最高。拿 1000W 的数据来说，需要的访问次数大约为 log10000000 = 24 次。用时约 12*24 = 288ms，这还是我们对系统拥有完整控制资源的情况下。

如何使访问次数低于 24，很明显我们要构造 M 叉查找树。在二叉树中我们需要一个键来决定到底取用两个分支中的哪个，而在 M 叉查找树中需要 M-1 个键来决定选取哪个分支，同时需要保证 M 叉查找树以某种方式得到平衡。

实现这种想法的一种方法是使用 M 阶 B 树：

（1）数据项存储在树叶上。

（2）非叶结点存储直到 M-1 个键，以指示搜索的方向；键 i 代表子树 i+1 中的最小的键。

（3）树的根要么是一片树叶，要么其儿子数在 2 和 M 之间。

（4）除根外，所有非叶结点的儿子数在 $\left \lceil M/2 \right \rceil$ 和 M 之间。（保证其不会退化为二叉树）

（5）所有的树叶都在相同的深度上并有 $\left \lceil L/2 \right \rceil$ 和 L 之间个数项，稍后描述 L。

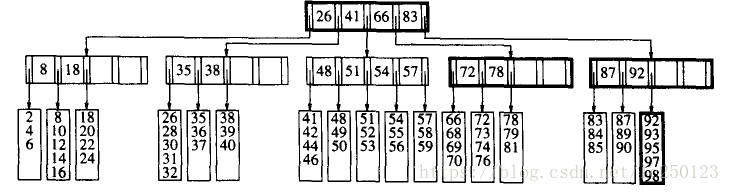
以下是一个 5 阶 B 树的一个例子（L = 5）：

如何确定 L 值：

一个结点代表一个磁盘区块，假设一个区块容纳 8192 字节，一个键值假设为 32 字节（比如身份证号占 17 字节），在一个 M 阶的 B 树中，我们有 M-1 个键，总数占 32M-32 字节，然后有 M 个分支，由于每个分支基本上都是别的区块，因此我们可以假设一个分支就像一个指针，占 4 个字节，这样总共 36M-32 字节，那么不超过 8192 的最大 M 值为 228。假设一个数据记录占 256 字节，那么一个区块最多能装 32 个记录，如是 L=32。这样就保证每片树叶有 16 到 32 个数据记录以及每个内部结点（除根外）至少以 114 种方式分叉。如果有 1000W 记录，那么至多存在 1e7 / 16 = 625000 片树叶。在最坏情况下树叶将在第 4 层上（近似 $log_{(M/2)}N$ ）。同时我们也可以将根节点和下一层存放在内存以提升速率。

对 B 树的插入和删除：

插入时要考虑树叶是否装满，满后分裂为两片树叶，考虑父节点儿子个数是否已满，父节点已满就分裂父节点，同理往上，如果达到根结点满，就分裂根结点，然后添加一个新根。还有一种方法处理儿子过多的情况，就是在相邻结点有空间时把一个儿子过继过去。

删除时要考虑叶结点小于 $\left \lceil L/2 \right \rceil$ 的情况，我们可以在没有达到 L 值时合并一个邻项来矫正，如果最终导致根结点只有一个儿子，就删除根节点。如下是删除 99 后的情况：

树在标准库中的应用

下面两个 STL 容器都是由自顶向下红黑树实现的：

set 容器：set 是一个排序后的容器，该容器不允许重复。

map 容器：map 用来存储排序后的由键和值组成的项的集合。键必须唯一，但是多个键可以对应同一个值。因此，值不需要唯一。在 map 中的键保持逻辑排序后的顺序。

map 中需要注意的地方：

map 中有一个重要的操作符重载： ValueType & operator[] ( const KeyType & key ); 其有改变 map 本身的功能，如果 map 中存在这个 key，就返回指向相应的值的引用。如果 map 中不存在 key，就在 map 中插入一个默认的值，然后返回指向这个插入的默认值的引用。所以如果函数中传入的是 const map 就不要使用这个功能。

map<string, double> salaries;

salaries["Pat"] = 7500.00;
cout << salaries["Pat"] << endl;
cout << salaries["Jan"] << endl;

输出：
7500.00
0

【数据结构与算法】第4章 树

树的实现

二叉树

查找树 ADT -- 二叉查找树

AVL 树

伸展树

B 树

树在标准库中的应用

【数据结构与算法】第4章树