随机变量的定义分类和各种主要概率密度分布介绍

目录

1 随机变量的定义

随机变量

分布函数

分布函数的基本性质

2 离散型随机变量及其分布

二项分布

泊松分布

3连续型随机变量及其分布

定义和概率密度的性质

均匀分布

正态分布

标准正态分布

Γ分布和指数分布

---

本文你主要讲解了随机变量，分布函数的定义及基本性质；离散型随机变量的二项分布和泊松分布；连续型随机变量的定义，概率密度的性质，以及主要的均匀分布，正态分布，标准正态分布，Γ分布和指数分布。

1 随机变量的定义

随机变量

设E是随机试验,它的样本空间S={e}, 如果对于每一个 e∈S, 有一个实数X(e)与之对应，这样就得到定义在样本空间S上的单值实函数X=X(e),称X=X(e)为随机变量。

随机变量分为两类：离散型随机变量和非离散型随机变量。

非离散型随机变量最常见的是连续型随机变量。

分布函数

设X是一个随机变量，x是任意实数，称函数

为随机变量X的分布函数。

由分布函数的定义可知，对任意实数a,b,有

分布函数的基本性质

2 离散型随机变量及其分布

二项分布

设随机变量X具有分布律

其中 0<p<1为常数，则称X服从参数为n,p的二项分布，记为 X ~ B(n,p)

二项分布是专门用来描述只有“成功”和“失败”两种结果的数学模型。

泊松分布

设随机变量X的分布律为

其中λ>0, 则称X服从参数为λ的泊松分布，记为X~P(λ)

泊松定理：

设随机变量Xn (n=1,2,…)服从二项分布，其分布律为

又设pn=λ>0(n=1,2,…)是常数，则有：

3连续型随机变量及其分布

定义和概率密度的性质

设随机变量X的分布函数为F(x), 若存在非负可积函数f(x), 使对于任意实数x， 有

则称X为连续型随机变量，f(x)称为X的概率密度函数，简称概率密度。

 

概率密度f(x)具有以下性质：

概率密度的图形称为分布曲线，性质（1）表示分布曲线位于x轴的上方。

均匀分布

如果随机变量X的概率密度为

则称X在(a,b)上服从均匀分布，记为X~U(a,b)

服从均匀分布的概率密度的图形为：

正态分布

如果随机变量X的概率密度为

其中, 则称X服从参数为 的正态分布，记为 .

正态分布又称为高斯分布，f(x)的图形为：

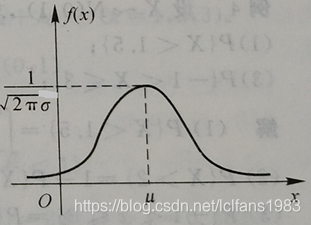
如图可知，f(x)在x=μ处达到最大值

正态分布概率密度曲线的这种“中间高，两头低”的特点反映了在正常状态下一般事物所遵循的客观规律。例如一大群人的身高，特别高大和特别矮小者占少数，而处于中间状态者居多；各种职业的人的合法收入等。

标准正态分布

当μ=0， δ2=1时的正态分布N(0,1)称为标准正态分布。记为X~N(0,1)

通常用φx, Φ(x)分别表示其概率密度和分布函数

标准正态分布的图形函数为：

Γ分布和指数分布

如果随机变量X的概率密度为：

则称X服从分布，记为

 

当分布的概率密度为：

此时称随机变量X服从参数为β的指数分布