AI编程方法案例：决策树的生成-CSDN博客

本文链接：https://blog.csdn.net/leeshuqing/article/details/147411646

利用递归函数可以实现决策树生成。

主要过程包括：

①实现基尼不纯度的计算，该指标可以衡量数据集纯度的一个指标，值越低表示数据集越纯净。当完全纯净时表示已经无需再进行判断分支的添加。

首先确定标签列表中有多少种类，对于每个标签类别，分别计算它在标签列表中出现的次数占总样本数的比例。通过计算每个类别比例的平方和，然后用1减去这个和，得到基尼不纯度值。计算公式为：

$G=1-\sum_{i=1}^{C}P(i)^{_{2}}$

其中C为不同类别的总数，P(i)是第i个类别的出现比率。

②实现最佳分割点，通过遍历每个特征所有可能的分割点，计算每个分割点的基尼不纯度，并选择基尼不纯度最低的分割点作为最佳分割点。

首先对于每个特征（通过i索引），获取该特征的所有唯一值作为可能的阈值，并使用相邻两个阈值平均值作为候选阈值。其次，对于每个候选阈值，将数据集分为左子集和右子集。如果某个子集为空，则跳过该阈值。同时，计算左子集和右子集的基尼不纯度，并加权求和得到总的基尼不纯度。最后，如果当前阈值的基尼不纯度小于当前最优的基尼不纯度，则确定最优分割点。

③递归构建决策树，根据设定的最大深度或数据集无法进一步分割（所有标签都相同或者基尼不纯度为0）的情况停止递归，并返回叶节点的值。否则，它会找到最佳分割点，分割数据集，并递归地构建左右子树。

已有电商企业订货数据，给出了该企业商品采购与否的已有情况：

特征				标签
采购价格	进口税率	预定用户数	存储费用	是否采购
50	0.03	60	30	不采购
100	0.06	100	20	不采购
210	0.03	250	30	不采购
200	0.03	450	30	不采购
220.3	0.09	500	20	不采购
150	0.03	50	30	采购
210	0.03	90	30	采购
320	0.03	100	30	采购
120	0.03	285	30	采购
21.6	0.03	450	30	采购
80	0.03	500	20	采购
155	0.06	500	30	采购
80	0.03	510	20	采购
91	0.09	520	30	采购

对于利用递归函数生成决策树，AI编程工具都可以很方便的予以实现。但是由于不同的决策树算法可能会因为算法过程、参数设定等不同而使得代码并不会功能完全一致。因此，这里提出几个重要的建议：

①如果确定所使用的决策树算法的具体细节，一定要把细节文字作为提示词内容，否则代码实现功能可能会有所差别。比如上述提到的各种计算方法。

②对于AI生成的代码，未必一定较好，比如对于gini_impurity函数，可能的一个版本是：

def gini_impurity(labels):
    """计算一组标签的基尼不纯度"""
    m = len(labels)
    return 1 - sum((sum(1 for _ in range(labels.count(c))) / m) ** 2 for c in set(labels))

此时可以看出第4行累加1的过程其实没有意义，直接使用累加即可。

def gini_impurity(labels):
    m = len(labels)
    return 1 - sum((labels.count(c) / m) ** 2 for c in set(labels))

这在一定程度上也说明，AI编程工具生成的代码在质量上可能并非最优，甚至其实现思路都迥异于常规思路。

再比如对于best_split函数，可能的一个版本是：

# 找到最佳分割点（简化的决策树分裂函数）
def best_split(X, y):
    """"""
    best_gini = 1.0
    best_feature = None
    best_threshold = None

    # 遍历每个特征和可能的分割点
    for i in range(len(X[0])):
        # 获取该特征的所有唯一值作为可能的阈值
        thresholds = sorted(set(row[i] for row in X))
        for j in range(len(thresholds) - 1):
            # 使用两个相邻值的平均值作为阈值
            threshold = (thresholds[j] + thresholds[j + 1]) / 2

            left_mask = [row[i] <= threshold for row in X]
            right_mask = [not lm for lm in left_mask]

            # 如果某个子集为空，则跳过该分割点
            if sum(left_mask) == 0 or sum(right_mask) == 0:
                continue

            left_labels = [y[k] for k, lm in enumerate(left_mask) if lm]
            right_labels = [y[k] for k, rm in enumerate(right_mask) if rm]

            # 计算基尼不纯度
            gini = (sum(left_mask) / len(y)) * gini_impurity(left_labels) + \
                   (sum(right_mask) / len(y)) * gini_impurity(right_labels)

            # 找到最佳分割点
            if gini < best_gini:
                best_gini = gini
                best_feature = i
                best_threshold = threshold

    return best_gini, best_feature, best_threshold

在该代码中，best_split函数对于每个特征，都会循环遍历每个可能的获选阈值。对于特定的阈值，此时需要得到y标签列表中对应的各个标签。为此在第16行和17行代码中，通过设置left_mask和right_mask列表，使用True和False分别标注左右子树的节点内容，然后在第23和24行再去y标签中去除相应的元素。这充分体现了Pythonic的编程风格，但是也导致代码可读性不高。

不过，即使如此，也可以对AI编程工具生成的代码让其自己去调整。比如对于上述best_split函数，可以通过提示词“将best_split函数中通过left_mask和right_mask间接获取left_labels和right_labels的代码写成直接获取的代码”，就可以得到可取的代码。改进的代码为：

def best_split(X, y):
    best_gini = 1.0
    best_feature = None
    best_threshold = None

    # 遍历每个特征和可能的分割点
    for i in range(len(X[0])):
        thresholds = sorted(
            set(row[i] for row in X))
        for j in range(len(thresholds) - 1):
            # 使用两个相邻值的平均值作为阈值
            threshold = (thresholds[j] + thresholds[j + 1]) / 2

            # 将数据集分割为左右子集
            left_labels = []
            right_labels = []
            for row, label in zip(X, y):
                if row[i] <= threshold:
                    left_labels.append(label)
                else:
                    right_labels.append(label)

            # 如果某个子集为空，则跳过该分割点
            if not left_labels or not right_labels:
                continue

            # 计算基尼不纯度
            gini = (len(left_labels) / len(y)) * gini_impurity(left_labels) + \
                   (len(right_labels) / len(y)) * gini_impurity(right_labels)

            # 找到最佳分割点
            if gini < best_gini:
                best_gini = gini
                best_feature = i
                best_threshold = threshold

    return best_gini, best_feature, best_threshold

③AI编程工具在整个开发过程中的应用面很广，再如对于表格数据，据此得到X特征列表，编写工作量既大又容易出错，可以在附加数据内容后使用提示词“将下面数据转换为一个Python的二维列表”即可自动生成Python列表代码。但是对于此类数据，仍然建议读者要仔细核实下个数和是否正确。

不仅如此，AI编程工具还可以很好的总结现有代码的功能。比如对于gini_impurity函数，如果不是很能理解计算过程，可以使用提示词“给出gini_impurity函数的计算思路”。如果要得到纯粹的文本说明，还可以使用提示词“使用200字的汉字、不使用任何公式和字母来描述gini_impurity实现思路”等等，都可以取得良好的效果。

最后附完整代码：

# 计算一组标签的基尼不纯度
def gini_impurity(labels):
    m = len(labels)
    return 1 - sum((labels.count(c) / m) ** 2 for c in set(labels))

# 找到最佳分割点（简化的决策树分裂函数）
def best_split(X, y):
    best_gini = 1.0
    best_feature = None
    best_threshold = None

    # 遍历每个特征和可能的分割点
    for i in range(len(X[0])):
        thresholds = sorted(
            set(row[i] for row in X))
        for j in range(len(thresholds) - 1):
            # 使用两个相邻值的平均值作为阈值
            threshold = (thresholds[j] + thresholds[j + 1]) / 2

            # 将数据集分割为左右子集
            left_labels = []
            right_labels = []
            for row, label in zip(X, y):
                if row[i] <= threshold:
                    left_labels.append(label)
                else:
                    right_labels.append(label)

            # 如果某个子集为空，则跳过该分割点
            if not left_labels or not right_labels:
                continue

            # 计算基尼不纯度
            gini = (len(left_labels) / len(y)) * gini_impurity(left_labels) + \
                   (len(right_labels) / len(y)) * gini_impurity(right_labels)

            # 找到最佳分割点
            if gini < best_gini:
                best_gini = gini
                best_feature = i
                best_threshold = threshold

    return best_gini, best_feature, best_threshold

# 递归地分割数据集以构建决策树
def recursive_tree_split(X, y):
    # 达到最大深度或无法进一步分割（所有标签都相同），返回叶节点的值
    if  len(set(y)) == 1:
        return {'叶节点的值为：': max(set(y), key=y.count)}

    # 找到最佳分割点
    best_gini, best_feature, best_threshold = best_split(X, y)

    # 如果无法找到有效的分割点，返回叶节点的值（多数类）
    if best_feature is None:
        return {'叶节点的值为：': max(set(y), key=y.count)}

        # 分割数据集
    left_X = []
    right_X = []
    left_y = []
    right_y = []
    for row, label in zip(X, y):
        if row[best_feature] <= best_threshold:
            left_X.append(row)
            left_y.append(label)
        else:
            right_X.append(row)
            right_y.append(label)

    # 递归地构建左右子树
    left_subtree = recursive_tree_split(left_X, left_y)
    right_subtree = recursive_tree_split(right_X, right_y)

    # 返回节点信息
    return {
        '特征序号：': best_feature,
        '阈值：': best_threshold,
        '左子树：': left_subtree,
        '右子树：': right_subtree
    }
# 特征矩阵
X = [
    [50, 0.03, 60, 30], [100, 0.06, 100, 20], [210, 0.03, 250, 30],
    [200, 0.03, 450, 30], [220.3, 0.09, 500, 20], [150, 0.03, 50, 30],
    [210, 0.03, 90, 30], [320, 0.03, 100, 30], [120, 0.03, 285, 30],
    [21.6, 0.03, 450, 30], [80, 0.03, 500, 20], [155, 0.06, 500, 30],
    [80, 0.03, 510, 20], [91, 0.09, 520, 30]]

# 标签向量
y = [
    '不采购', '不采购', '不采购', '不采购', '不采购', '采购', 
    '采购', '采购', '采购', '采购', '采购', '采购', '采购', '采购'
]

# 构建决策树
tree = recursive_tree_split(X, y)
print(tree)

运行结果为：

{'特征序号：': 0, '阈值：': 177.5,

'左子树：': {'特征序号：': 2, '阈值：': 192.5,

'左子树：': {'特征序号：': 0, '阈值：': 125.0,

'左子树：': {'叶节点的值为：': '不采购'},

'右子树：': {'叶节点的值为：': '采购'}},

'右子树：': {'特征序号：': 2, '阈值：': 175.0,

'左子树：': {'叶节点的值为：': '采购'},

'右子树：': {'叶节点的值为：': '不采购'}}}

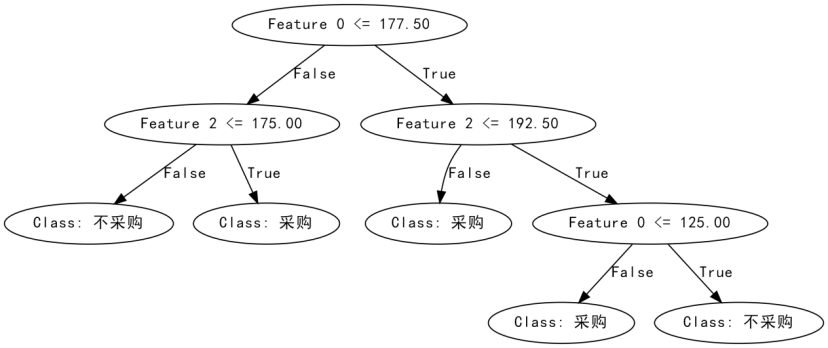
通过一些可视化绘制工具包，可以得到：