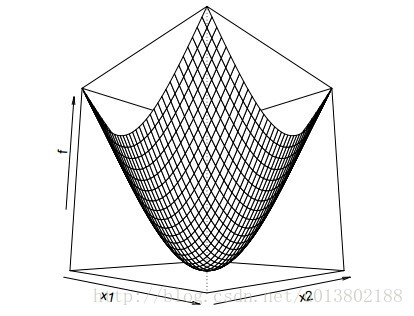
问题的描述:给定一个可微的凸函数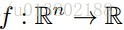
形式化的描述为:是不是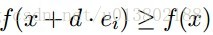
这里的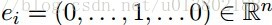
答案为成立。
这是因为:
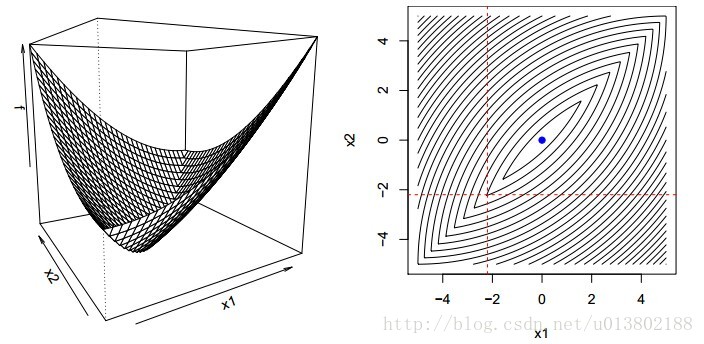
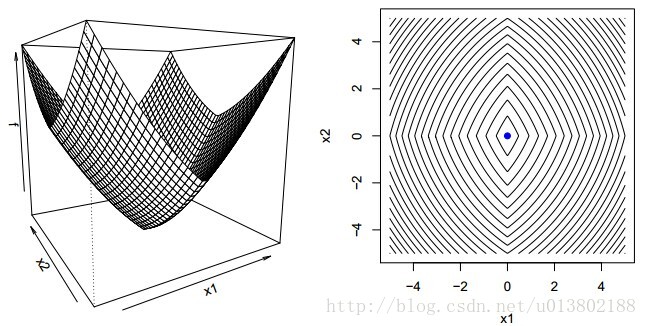
但是问题来了,如果对于凸函数f,若不可微该会怎样呢?
答案为不成立,上面的图片就给出了一个反例。
那么同样的问题,现在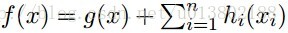
答案为成立。
证明如下,对每一个y
坐标下降(Coordinate descent):
这就意味着,对所有的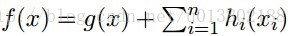
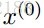
每一次我们解决了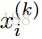
Tseng (2001)的开创性工作证明:对这种f(f在紧集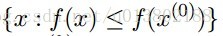

在实分析领域:
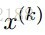
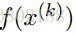
其中:
坐标下降的顺序是任意的,可以是从1到n的任意排列。
可以在任何地方将单个的坐标替代成坐标块
关键在于一次一个地更新,所有的一起更新有可能会导致不收敛
我们现在讨论一下坐标下降的应用:
线性回归:
令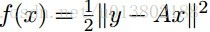
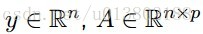
最小化xi,对所有的xj,j不等于i:
解得:
坐标下降重复这个更新对所有的
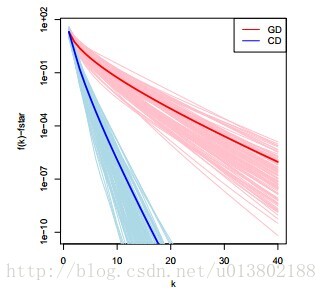
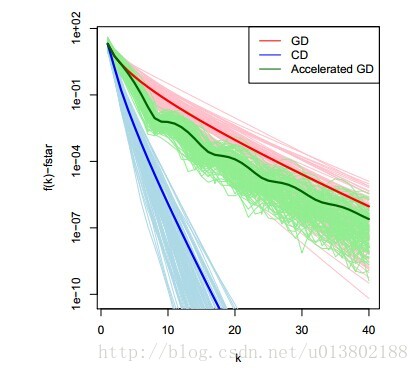
对比坐标下降与梯度下降在线性回归中的表现(100个实例,n=100,p=20)
将坐标下降的一圈与梯度下降的一次迭代对比是不是公平呢?是的。
其中r=y-Ax。每一次的坐标更新需要O(n)个操作,其中O(n)去更新r,O(n)去计算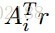
我们用相同的例子,用梯度下降进行比较,似乎是与计算梯度下降的最优性相违背。
那么坐标下降是一个一阶的方法吗?事实上不是,它使用了比一阶更多的信息。
现在我们再关注一下支持向量机:
SVM对偶中的坐标下降策略:
SMO(Sequentialminimal optimization)算法是两块的坐标下降,使用贪心法选择下一块,而不是用循环。
回调互补松弛条件(complementaryslackness conditions):
v,d,s是原始的系数,截距和松弛,其中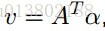
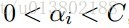
SMO重复下面两步:
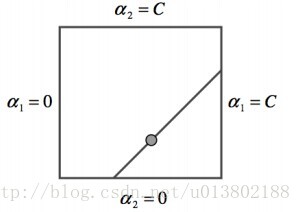
选出不满足互补松弛的αi,αj
最小化αi,αj使所有的变量满足条件
第一步使用启发式的方法贪心得寻找αi,αj,第二步使用等式约束。











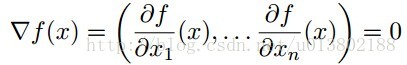
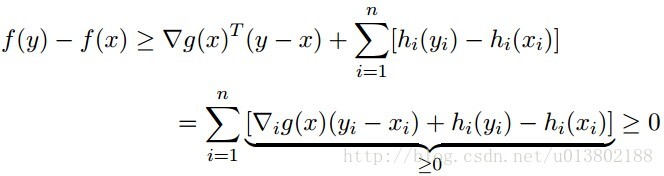
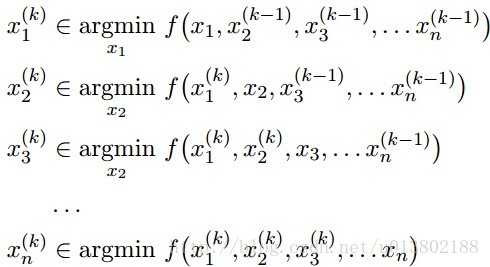
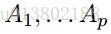
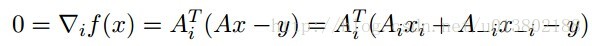
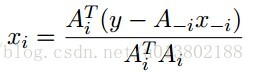
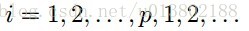
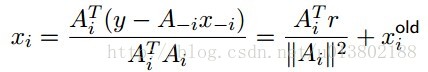

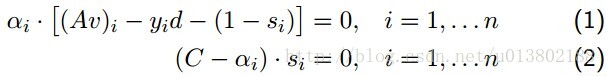














 4万+
4万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








