特征向量的几何含义

本文转自甜蜜旮旯的博客：http://fanhy298.blog.sohu.com/130363634.html

长时间以来一直不了解矩阵的特征值和特征向量到底有何意义（估计很多兄弟有同样感受）。知道它的数学公式，但却找不出它的几何含义，教科书里没有真正地把这一概念从各种角度实例化地进行讲解，只是一天到晚地列公式玩理论——有个屁用啊。

根据特征向量数学公式定义，矩阵乘以一个向量的结果仍是同维数的一个向量，因此，矩阵乘法对应了一个变换，把一个向量变成同维数的另一个向量，那么变换的效果是什么呢？这当然与方阵的构造有密切关系，比如可以取适当的二维方阵，使得这个变换的效果就是将平面上的二维向量逆时针旋转30度，这时我们可以问一个问题，有没有向量在这个变换下不改变方向呢？可以想一下，除了零向量，没有其他向量可以在平面上旋转30度而不改变方向的，所以这个变换对应的矩阵(或者说这个变换自身)没有特征向量(注意：特征向量不能是零向量)，所以一个变换的特征向量是这样一种向量，它经过这种特定的变换后保持方向不变，只是进行长度上的伸缩而已(再想想特征向量的原始定义Ax=cx, cx是方阵A对向量x进行变换后的结果，但显然cx和x的方向相同)。

这里给出一个特征向量的简单例子，比如平面上的一个变换，把一个向量关于横轴做镜像对称变换，即保持一个向量的横坐标不变，但纵坐标取相反数，把这个变换表示为矩阵就是[1 0;0 -1]（分号表示换行），显然[1 0;0 -1]*[a b]'=[a -b]'（上标'表示取转置），这正是我们想要的效果，那么现在可以猜一下了，这个矩阵的特征向量是什么?想想什么向量在这个变换下保持方向不变，显然，横轴上的向量在这个变换下保持方向不变(记住这个变换是镜像对称变换，那镜子表面上(横轴上)的向量当然不会变化)，所以可以直接猜测其特征向量是[a 0]'（a不为0），还有其他的吗？有，那就是纵轴上的向量，这时经过变换后，其方向反向，但仍在同一条轴上，所以也被认为是方向没有变化，所以[0 b]'（b不为0）也是其特征向量。

综上，特征值只不过反映了特征向量在变换时的伸缩倍数而已，对一个变换而言，特征向量指明的方向才是很重要的，特征值似乎不是那么重要；但是，当我们引用了Spectral theorem（谱定律）的时候，情况就不一样了。

Spectral theorem的核心内容如下：一个线性变换（用矩阵乘法表示）可表示为它的所有的特征向量的一个线性组合，其中的线性系数就是每一个向量对应的特征值，写成公式就是：

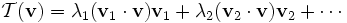
从这里我们可以看出，一个变换（矩阵）可由它的所有特征向量完全表示，而每一个向量所对应的特征值，就代表了矩阵在这一向量上的贡献率——说的通俗一点就是能量（power），至此，特征值翻身做主人，彻底掌握了对特征向量的主动：你所能够代表这个矩阵的能量高低掌握在我手中，你还吊什么吊？

我们知道，一个变换可由一个矩阵乘法表示，那么一个空间坐标系也可视作一个矩阵，而这个坐标系就可由这个矩阵的所有特征向量表示，用图来表示的话，可以想象就是一个空间张开的各个坐标角度，这一组向量可以完全表示一个矩阵表示的空间的“特征”，而他们的特征值就表示了各个角度上的能量（可以想象成从各个角度上伸出的长短，越长的轴就越可以代表这个空间，它的“特征”就越强，或者说显性，而短轴自然就成了隐性特征），因此，通过特征向量/值可以完全描述某一几何空间这一特点，使得特征向量与特征值在几何（特别是空间几何）及其应用中得以发挥。

关于特征向量（特别是特征值）的应用实在是太多太多，近的比如俺曾经提到过的PCA方法，选取特征值最高的k个特征向量来表示一个矩阵，从而达到降维分析+特征显示的方法；近的比如Google公司的成名作PageRank，也是通过计算一个用矩阵表示的图（这个图代表了整个Web各个网页“节点”之间的关联）的特征向量来对每一个节点打“特征值”分；再比如很多人脸识别，数据流模式挖掘分析等方面，都有应用，有兴趣的兄弟可以参考IBM的Spiros在VLDB‘ 05，SIGMOD ’06上的几篇文章。

特征向量不仅在数学上，在物理，材料，力学等方面（应力、应变张量）都能一展拳脚，有老美曾在一本线代书里这样说过“有振动的地方就有特征值和特征向量”，确实令人肃然起敬+毛骨悚然......