HDU 5728 PowMod （欧拉函数+指数循环节）

PowMod （点击打开题目）

Time Limit: 3000/1500 MS (Java/Others)    Memory Limit: 262144/262144 K (Java/Others)
Total Submission(s): 840    Accepted Submission(s): 291

Problem Description

Declare:
k=∑mi=1φ(i∗n) mod 1000000007
n is a square-free number.
φ is the Euler's totient function.
find:
ans=kkkk...k mod p
There are infinite number of k

Input

Multiple test cases(test cases ≤100 ), one line per case.
Each line contains three integers, n,m and p .

1≤n,m,p≤107

Output

For each case, output a single line with one integer, ans.  

Sample Input

  
  

   
   1 2 6
1 100 9
  
  

Sample Output

  
  

   
   4
7
  
  

Author

HIT

Source

2016 Multi-University Training Contest 1

Recommend

wange2014   |   We have carefully selected several similar problems for you:  5775 5774 5773 5772 5771 

 

题意：定义以下公式：

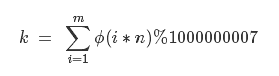
给出： n,m,p ，且 n 无平方因子。

要你求出：

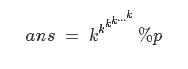 （k有无限个）

题解： 欧拉函数 + 指数循环节。

1.欧拉函数：求出K。

　　          定理： 欧拉函数是非完全积性函数: φ(m*n) = φ(n)*φ(m) , 当且仅当GCD(n,m) = 1.

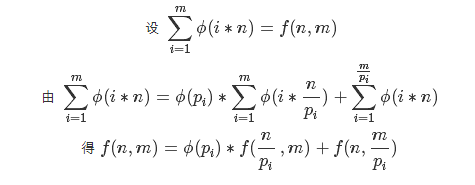
由以上公式可算出K。

2. 指数循环节：将指数循环节化无限为有限，具体实现为递归操作。递归出口为 φ(p)=1。

                          指数循环节：

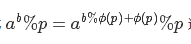                                              递归计算就可以了。

普及：

-----------------------------------------------------------------------------------------------------------------------------------

欧拉函数：
对正整数n，欧拉函数是少于或等于n的数中与n互质的数的数目。   例如euler(8)=4，因为1,3,5,7均和8互质。

通式：
    对于一个正整数N的素数幂分解    N = (P1^q1) * (P2^q2) * ...* (Pn^qn).
        φ(1) = 1.
        φ(N) = N * (1-1/P1) * (1-1/P2) *...* (1-1/Pn).

定理：
    1.欧拉函数是非完全积性函数: φ(m*n) = φ(n)*φ(m) , 当且仅当GCD(n,m) = 1.
    
    2.一个数的所有质因子之和是  phi(n)*n/2.
    
    3.若n是素数p的k次幂，φ(n)=p^k-p^(k-1)=(p-1)p^(k-1)，因为除了p的倍数外，其他数都跟n互质.
    
特殊性质： 
    1.当n为奇数时，φ(2n) = φ(n).
    2.对于质数p，φ(p) = p - 1
    3.除了N=2,φ(N)都是偶数.
    
指数循环节：
    A^x = A^(x % φ(C) + φ(C)) (mod C)  (x >= φ(C)) 

定理1 应用：
    ∑(i=1,m)φ(i*n) = φ(pi) * ∑(i=1,m)φ(i*n/pi) + ∑(i=1,m/pi)φ(i*n) ; (n无平方因子数)

------------------------------------------------------------------------------------------------------------------------------------

AC代码：

#include <bits/stdc++.h>
using namespace std;
const int MOD= 1000000007;
const int MAXN=1e7;
int phi[MAXN+5];
long long sum[MAXN+5];
long long k,n,m,p;
void GetEuler()
{
    memset(phi,0,sizeof(phi));
    phi[1]=1;
    for(int i = 2;i <= MAXN;i++)
        if(!phi[i])
            for(int j = i;j <= MAXN;j += i)
            {
                if(!phi[j]) phi[j]=j;
                phi[j] = phi[j] / i * (i-1);
            }
    sum[1]=1;
    for(int i = 2;i <=MAXN; i++)
        sum[i] = (sum[i-1] + phi[i]) % MOD;
}
long long Get_K(long long n,long long m)
{
    if(m==0) return 0;
    if(m==1) return phi[n];
    if(n==1) return sum[m];
    if(phi[n]==n-1) return (phi[n]*Get_K(1,m)%MOD + Get_K(n,m/n))%MOD;
    for(int i=2;i<MAXN;i++)
        if(n%i==0)
            return (phi[i] * Get_K(n/i,m)%MOD + Get_K(n,m/i) ) % MOD;
}
long long PowMod(long long a,long long b, long long mod)
{
    long long ans = 1;
    while(b)
    {
        if(b&1) ans = (ans*a)%mod;
        a= (a*a)%mod;
        b>>=1;
    }
    return ans;
}
long long Cal(long long k, long long p)
{
    if( p == 2) return k&1; //mod φ(p)
    return PowMod(k, Cal(k,phi[p])+phi[p], p); //递归的计算ans，递归出口为 φ(p)=1
}
int main()
{
    GetEuler(); //打表 
    while(~scanf("%lld%lld%lld",&n,&m,&p))
    {
        k = Get_K(n,m);
        printf("%lld\n",Cal(k,p));
    }
}