机器学习课程4-题1-1

薛毅书例9.2

解答过程：

输入数据

#### 输入数据, 按下三角输入, 构成向量
x<-c(1.00, 
     0.79, 1.00, 
     0.36, 0.31, 1.00, 
     0.96, 0.74, 0.38, 1.00, 
     0.89, 0.58, 0.31, 0.90, 1.00, 
     0.79, 0.58, 0.30, 0.78, 0.79, 1.00, 
     0.76, 0.55, 0.35, 0.75, 0.74, 0.73, 1.00, 
     0.26, 0.19, 0.58, 0.25, 0.25, 0.18, 0.24, 1.00,
     0.21, 0.07, 0.28, 0.20, 0.18, 0.18, 0.29,-0.04, 1.00,
     0.26, 0.16, 0.33, 0.22, 0.23, 0.23, 0.25, 0.49,-0.34, 1.00, 
     0.07, 0.21, 0.38, 0.08,-0.02, 0.00, 0.10, 0.44,-0.16, 0.23, 
     1.00, 
     0.52, 0.41, 0.35, 0.53, 0.48, 0.38, 0.44, 0.30,-0.05, 0.50, 
     0.24, 1.00, 
     0.77, 0.47, 0.41, 0.79, 0.79, 0.69, 0.67, 0.32, 0.23, 0.31, 
     0.10, 0.62, 1.00, 
     0.25, 0.17, 0.64, 0.27, 0.27, 0.14, 0.16, 0.51, 0.21, 0.15, 
     0.31, 0.17, 0.26, 1.00, 
     0.51, 0.35, 0.58, 0.57, 0.51, 0.26, 0.38, 0.51, 0.15, 0.29, 
     0.28, 0.41, 0.50, 0.63, 1.00, 
     0.21, 0.16, 0.51, 0.26, 0.23, 0.00, 0.12, 0.38, 0.18, 0.14, 
     0.31, 0.18, 0.24, 0.50, 0.65, 1.00)
#### 输入变量名称
names<-c("X1", "X2", "X3", "X4", "X5", "X6", "X7", "X8", "X9",  
         "X10", "X11", "X12", "X13", "X14", "X15", "X16")
#### 将矩阵生成相关矩阵
R<-matrix(0, nrow=16, ncol=16, dimnames=list(names, names))
for (i in 1:16){
   for (j in 1:i){
      R[i,j]<-x[(i-1)*i/2+j]; R[j,i]<-R[i,j]
   }
}

上面的三角矩阵转换为全矩阵，还有下面一种方法

#等同于下面
R1<-matrix(0, nrow=16, ncol=16, dimnames=list(names, names))
idx=0;
for (i in 1:16){
   for (j in 1:i){
      idx=idx+1;
      R1[i,j]<-x[idx]; R1[j,i]<-R1[i,j];

   }
}

主成分分析并分类

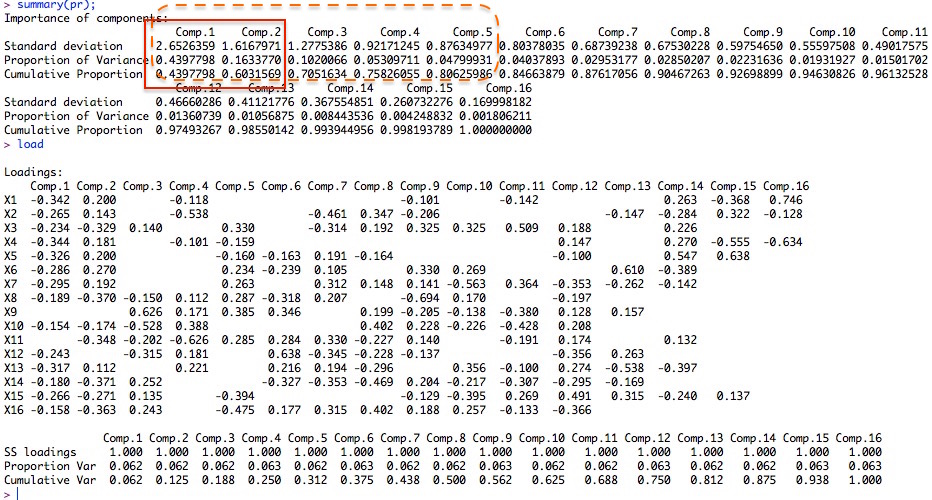
 #### 作主成分分析
pr<-princomp(covmat=R); load<-loadings(pr)
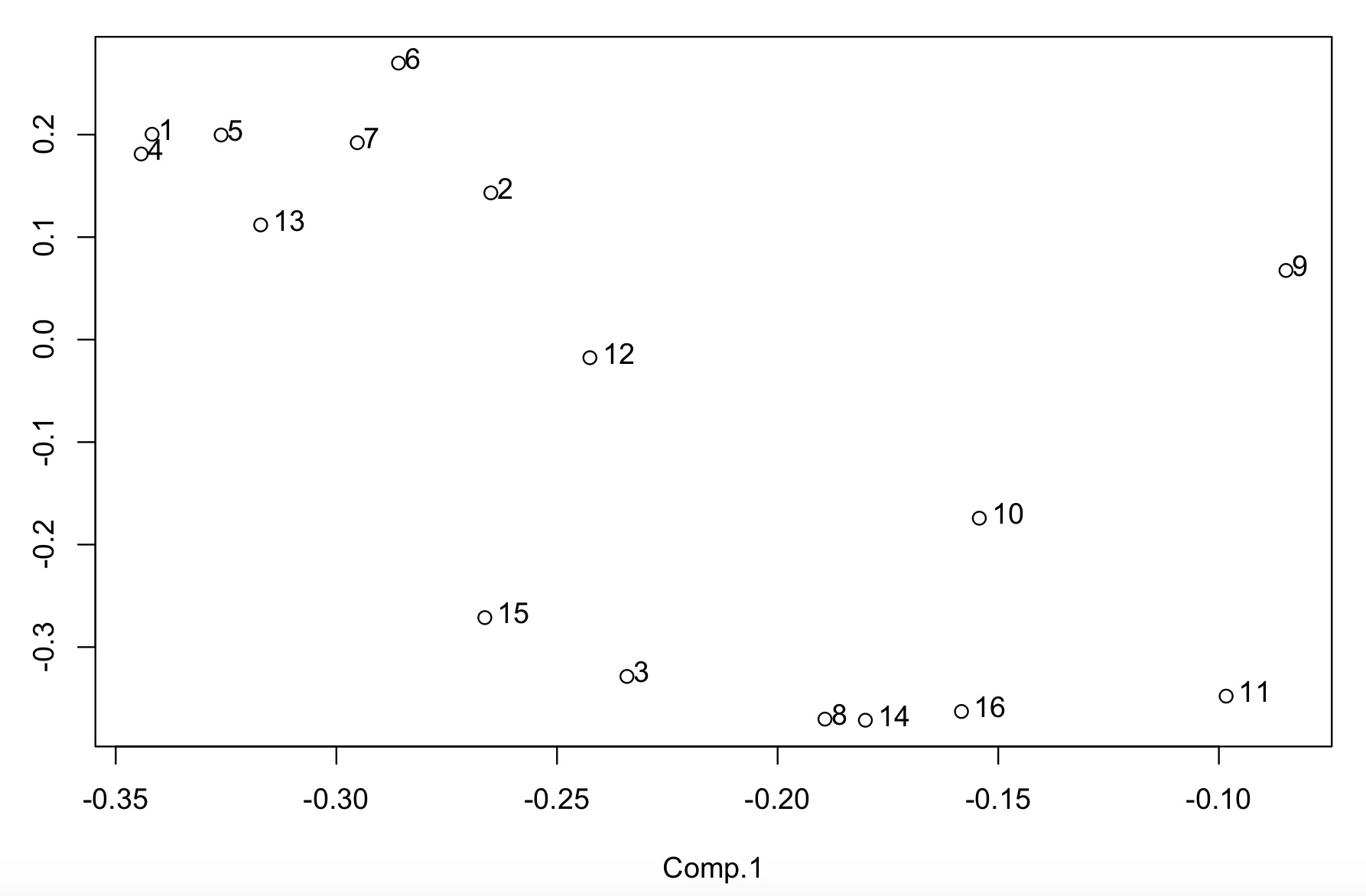
 #### 画散点图
plot(load[,1:2]); text(load[,1], load[,2], adj=c(-0.4, 0.3))

如下图所示，前5个因子的累计贡献率为0.8. 由于多维比较难画图，这儿只取前两个因子做散点图，然后进行分类。

结论与课本一致

• 左上角，长类
• 右下角 围类
• 中间，体型特征指标，即前胸(X₉）、后背(X_{10/sub>）、肩宽(X12)}

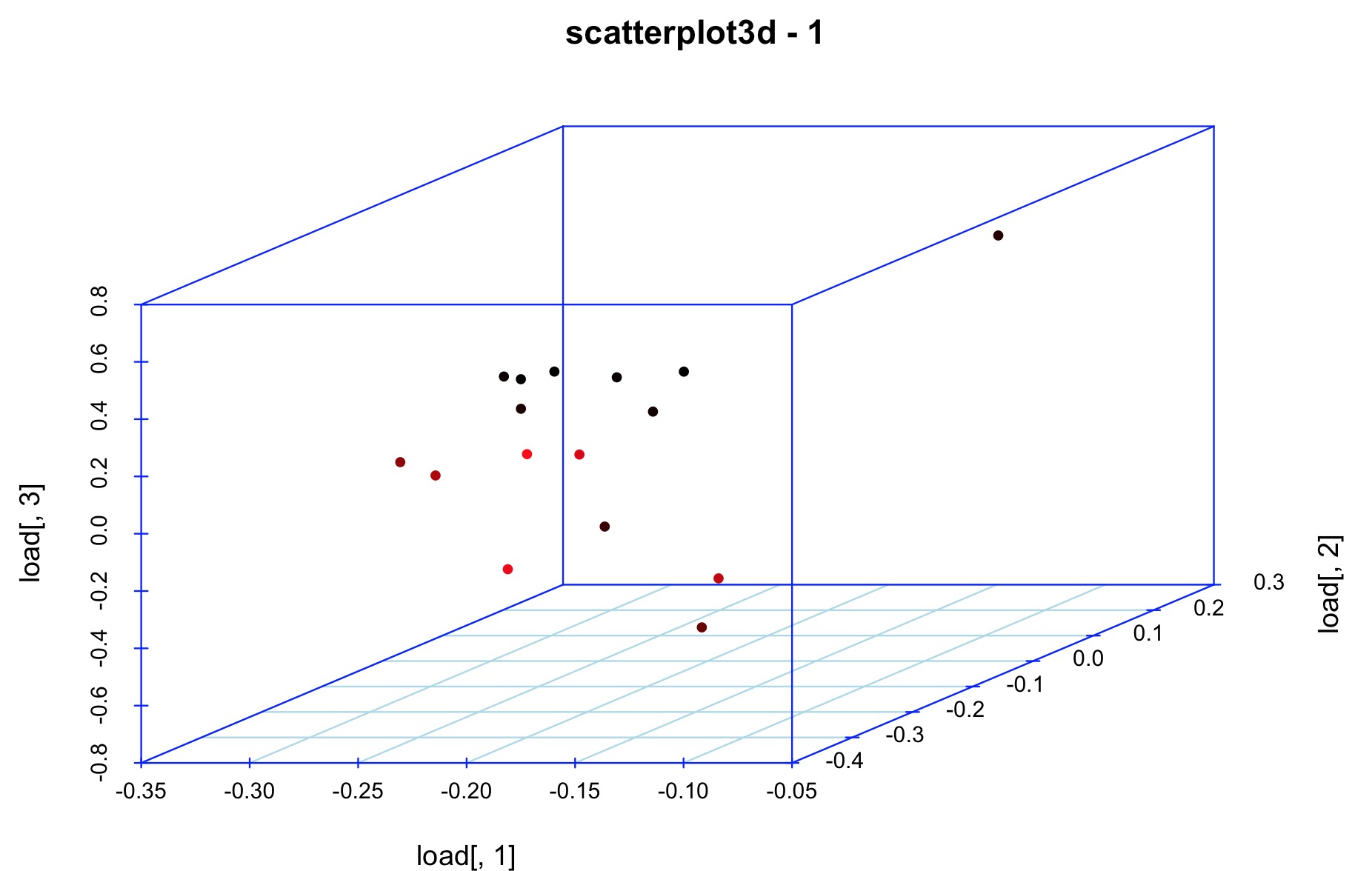
拓展：根据三个主成分画三维图

install.packages("scatterplot3d")
library(scatterplot3d)
scatterplot3d(load[,1],load[,2],load[,3],highlight.3d=TRUE, col.axis="blue",
       col.grid="lightblue", main="scatterplot3d - 1", pch=20);

三维图如上，业务上不好分析，仅参考用

总结，知识点如下

• 三角矩阵转为全矩阵
• 根据协方差阵做主成分分析
• 根据最主要两个主成分，做散点图，分类，并业务解释