poj 1149 PIGS 题解（网络流，建图）

LightningUZ

于 2019-08-10 21:41:18 发布

阅读量318

点赞数

分类专栏： POJ 文章标签：题解

本文链接：https://blog.csdn.net/lightninguz/article/details/99112324

版权

POJ 专栏收录该内容

13 篇文章

订阅专栏

博客介绍了如何使用网络流解决POJ 1149 PIGS问题，通过转换视角，将问题转化为每个猪被哪个人买，利用最大流的思想进行分配。建图策略包括拆点和根据顾客购买限制建立边，最后讨论了点数过多可能导致的问题并提出了缩点优化方法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

原题链接：
poj

题意简述

有 $m (< = 1000)$ 头猪，和 $n (< = 100)$ 个顾客。第 $i$ 个顾客有 $a_i(<=m)$ 个喜欢的猪（给定这些猪的编号），但是最多只会买 $b_i(<=m)$ 个。每种猪有 $v_i(<=1000)$ 个。合理分配，使得总共能卖出去的猪数量最多。

思路

最近是真正搞明白网络流（在教练的绝妙讲解下）。做了一些练习题。由于时间紧迫，这个是第一个能写出来博客的题目。（虽然不是第一个）

入正题。我们换一个角度考虑，我们不考虑每个人买哪些猪，我们考虑每个猪被哪个人买。设第 $i$ 个猪有 $c_i$ 个人买。由于猪 $i$ 只有 $v_i$ 个，然后我们要把 $v_i$ 分配给 $c_i$ 个人，使得在满足总和不超过 $c_i$ 个人的限制下最大。然后我们会发现，分配这件事情，不就是最大流中的一步么？

为什么是最大流中的一步：因为对于每个点都满足流量守恒（入流量=出流量），所以我们要合理分配这些进来的流，分配到若干个出去的流，使得最后流到汇点的流最大。所以分配这件事情就是我们在求最大流的时候，一个点要完成的任务。

所以考虑用最大流求解这个问题。但是由于我们还要满足每个人的购买上限，所以考虑拆点。

想到这样的建图方式：

每个猪要拆成 $n$ 个点。对于该猪的第 $i$ 个点，首先源点连到第 $1$ 个点，其权值是第 $i$ 头猪的数量 $v_i$ 。如果 $i$ 要买这头猪，那就连一条边权为 $i n f$ 的边过去。当然，这 $n$ 个点之间是以链的形式联通的，每条边都是正无穷。对于每个顾客，从这个点连到汇点，边权是这个顾客的购买上限。

图片（蒯来的，原地址：大佬博客）

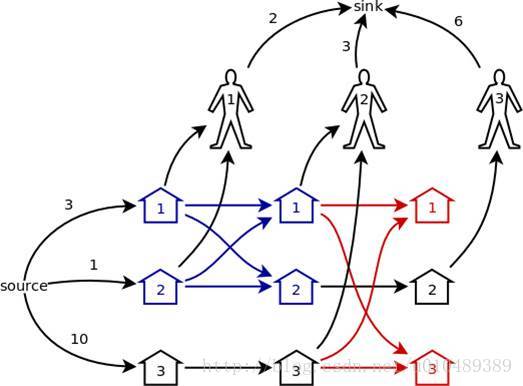
解释：
拆点是为了保证最大流过去能满足每个顾客的限制，防止某个顾客流过去的猪数量超过限制。 $n$ 个点之间链形联通是为了保证一头猪大家都珂以买。但是我们从源点到 $1$ 只有 $v_i$ 的流量，所以对于这一个猪，不珂能流到汇点的会大于 $v_i$ ，就满足了猪总数的限制。所以这个是对的

这个建图方法固然是对的，珂是点数是 $n m$ 级别的。虽然也许能过（BJOI的狼抓兔子就是一个栗子， $1 e 6$ 的点数 $D i n i c$ 水过），但是。。。 $p o j$ 的机哪能和洛谷的比。。。所以还是稳一点。所以我们要合并一些点。

观察到边很多是无穷，所以并不是所有的边都有用。用上面那个大佬博客里面的方法缩一下点，就能得到这样的图:

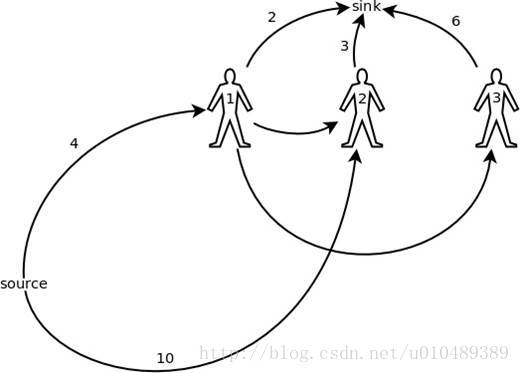
所以建边即可。然后我的代码 $T$ 了。。。求大家帮我找一下错。。。
如果想过了这个题，去借鉴一下上面那个巨佬的代码好了。。。
我的 $T L E$ 代码：

#include<cstring>
#include<cstdio>
#include<algorithm>
#include<vector>
#include<queue>
using namespace std;
namespace Flandle_Scarlet
{
    #define N 2010

    #define F(i,l,r) for(int i=l;i<=(r);++i)
    #define D(i,r,l) for(int i=r;i>=(l);--i)
    #define MEM(x,a) memset(x,a,sizeof(x))
    #define FK(x) MEM(x,0)
    class Graph
    {
        public:
            int EdgeCount;
            int head[N];
            struct Edge
            {
                int To,Label;
                int Next;
            }Ed[200100];
            void clear()
            {
                MEM(head,-1);
                MEM(Ed,-1);
                EdgeCount=-1;
            }
            void AddEdge(int u,int v,int w)
            {
                ++EdgeCount;
                Ed[EdgeCount]=(Edge){v,w,head[u]};
                head[u]=EdgeCount;
            }
            void AddFlow(int u,int v,int w)
            {
                AddEdge(u,v,w);
                AddEdge(v,u,0);
            }
            int Start(int u){return head[u];}
            int To(int i){return Ed[i].To;}
            int Label(int i){return Ed[i].Label;}
            int Next(int i){return Ed[i].Next;}

            int Source,Sink;
            int deep[N];
            queue<int>Q,EmptyQ;
            bool BFS()
            {
                Q=EmptyQ;
                FK(deep);

                Q.push(Source);
                deep[Source]=1;
                do
                {
                    int u=Q.front();Q.pop();
                    for(int i=head[u];~i;i=Ed[i].Next)
                    {
                        int v=Ed[i].To;
                        if (deep[v]==0 and Ed[i].Label>0)
                        {
                            deep[v]=deep[u]+1;
                            Q.push(v);
                        }
                    }
                }while(!Q.empty());

                if (deep[Sink]==0) return 0;
                return 1;
            }
            int DFS(int u,int MinFlow)
            {
                if (u==Sink) return MinFlow;
                for(int i=head[u];~i;i=Ed[i].Next)
                {
                    int v=Ed[i].To;
                    if (deep[v]==deep[u]+1 and Ed[i].Label!=0)
                    {
                        int d=DFS(v,min(MinFlow,Ed[i].Label));
                        if (d>0)
                        {
                            Ed[i].Label-=d;
                            Ed[i^1].Label+=d;
                            return d;
                        }
                    }
                }
                return 0;
            }
            int Dinic()
            {
                int ans=0;
                while(BFS())
                {
                    int d;
                    while(d=DFS(Source,0x3f3f3f3f))
                    {
                        ans+=d;
                    }
                }
                return ans;
            }
    }Nt;
    vector<int> buy[N];
    //buy[i]:costumers that will but pig_i
    int val[N];//val[i]:how many pigs in i
    int want[N];//want[i]:how many pigs i want
    int n,m;
    void R1(int &x)
    {
        x=0;char c=getchar();int f=1;
        while(c<'0' or c>'9') f=(c=='-')?-1:1,c=getchar();
        while(c>='0' and c<='9') x=(x<<1)+(x<<3)+(c^48),c=getchar();
        x=(f==1)?x:-x;
    }
    void Input()
    {
        F(i,1,m)
        {
            R1(val[i]);
        }

        F(i,1,n)
        {
            int cnt;R1(cnt);
            F(j,1,cnt)
            {
                int k;R1(k);
                buy[k].push_back(i);
            }
            R1(want[i]);
        }
    }

    #define S Nt.Source
    #define T Nt.Sink
    #define INF 0x3f3f3f3f
    void Soviet()
    {
        S=n+1,T=n+2;
        F(i,1,n)
        {
            Nt.AddFlow(i,T,want[i]);
        }
        F(i,1,m)
        {
            if (buy[i].size()>=2)
            {
                F(j,0,buy[i].size()-2)
                {
                    Nt.AddFlow(buy[i][j],buy[i][j+1],INF);
                }
            }

            if (buy[i].size()>0)
            {
                int first=buy[i][0];
                Nt.AddFlow(S,first,val[i]);
            }
        }
        printf("%d\n",Nt.Dinic());
    }

    void InitAll()
    {
        FK(val);
        FK(want);
        F(i,1,n) buy[i].clear();
        Nt.clear();
    }
    void IsMyWife()
    {
        if (0)
        {
            freopen("","r",stdin);
            freopen("","w",stdout);
        }
        while(~scanf("%d%d",&n,&m) and n+m)
        {
            InitAll();

            Input();
            Soviet();
        }

    }
};
int main()
{
    Flandle_Scarlet::IsMyWife();
    return 0;
}