图论
DFS
#include<iostream>
#include<stdio.h>
using namespace std;
int n,m,t,sx,sy,ex,ey;
int a[10][10];
int dir[4][2]={0,1,1,0,-1,0,0,-1};
int ans=0;
void dfs(int x,int y){
if(x==ex&&y==ey){
ans++;
return;
}
for(int i=0;i<4;i++){
int nx=x+dir[i][0],ny=y+dir[i][1];
if(nx>=1&&nx<=n&&ny>=1&&ny<=m&&a[nx][ny]==0){
a[nx][ny]=1;
dfs(nx,ny);
a[nx][ny]=0;
}
}
}
int main(){
cin>>n>>m>>t>>sx>>sy>>ex>>ey;
int tx,ty;
while(t--){
cin>>tx>>ty;
a[tx][ty]=-1;//障碍
}
a[sx][sy]=1;//已访问
dfs(sx,sy);
cout<<ans;
return 0;
}
BFS
单源BFS
BFS求的最短路径是指步数最少。
//节点结构
struct Node{
int x,y;
Node(int x,int y):x(x),y(y){}
bool operator == (const Node&A)const{
if(this->x==A.x&&this->y==A.y) return true;
return false;
}
};
//标记数组
bool visit[MAXW][MAXH]={false};
//记录路径
Node FatherNode[MAXW][MAXH];
Stack<Node> S;
//方向数组
int dir[4][2]={0,1,1,0,0,-1,-1,0};
bool BFS(Node &start,Node &end){
queue<Node> Q;
Node CurrentNode,AdjacentNode;
int i;
//将源点放进队列Q
Q.push(Vs);
visit[start.x][start.y]=true;
while(!Q.empty()){
//取出对头
CurrentNode=Q.front();
Q.pop();
//判断相邻节点是不是end,是就结束函数,不是就推进队列Q并设置为已访问
for(i=0;i<4;i++){
AdjacentNode=Node(CurrentNode.x+dir[i][0],CurrentNode.y+dir[i][1]);
if(AdjacentNode==end){
FatherNode[AdjacentNode.x][AdjacentNode.y]=CurrentNode;
return true;
}
if(IsValid(AdjacentNode)&&!visit[AdjacentNode.x][AdjacentNode.y]){
Q.push(AdjacentNode);
visit[AdjacentNode.x][AdjacentNode.y]=true;
FatherNode[AdjacentNode.x][AdjacentNode.y]=CurrentNode;
}
}
}
return false;
}
//回溯FatherNode打印出最短路径
void Back(){
Node t=FatherNode[4][4];
while(!(t.x==0&&t.y==0)){
S.push(t);
t=FatherNode[t.x][t.y];
}
}
多源BFS
题目大意是求一01矩阵中每一点到矩阵中所有为1的位置的最短距离,输出这个“距离矩阵”。
假设一个虚拟节点,到结点值为1的距离为0。我们就由多源转成了单源问题。
#include <iostream>
#include <algorithm>
#include <cstring>
#include<queue>
using namespace std;
const int N=1010;
int n,m;
char g[N][N];
int d[N][N];//到虚拟源点的最短距离
int dir[][2]= {-1,0,0,-1,1,0,0,1};
void bfs() {
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)
d[i][j]=-1;
queue<pair<int,int>> q;
//将所有为1的点加入队列
for(int i=0; i<n; i++)
for(int j=0; j<m; j++) {
if(g[i][j]=='1') {
q.push({i,j});
d[i][j]=0;
}
}
while(!q.empty()) {
auto t=q.front();
q.pop();
int x=t.first,y=t.second;
for(int i=0; i<4; i++) {
int a=x+dir[i][0],b=y+dir[i][1];
if(a>=0&&a<n&&b>=0&&b<m&&d[a][b]==-1) {
d[a][b]=d[x][y]+1;
q.push({a,b});
}
}
}
}
int main() {
scanf("%d%d",&n,&m);
for(int i=0; i<n; i++) scanf("%s",g[i]);
bfs();
for(int i=0; i<n; i++) {
for(int j=0; j<m; j++)
printf("%d ",d[i][j]);
puts("");
}
return 0;
}
BFS例题
八数码问题
#include<iostream>
#include<string>
#include<sstream>
#include<math.h>
#include<algorithm>
#include<map>
#include<vector>
#include<queue>
#include<set>
#include<unordered_map>
using namespace std;
string e="123804765",s;
queue<string> q;
unordered_map<string,int> m;
int dir[][2]={-1,0,0,-1,1,0,0,1};
int BFS(){
q.push(s);
m[s]=0;
while(!q.empty()){
auto cur=q.front();q.pop();
if(cur==e) return m[cur];
int zero_pos=cur.find('0');
int x=zero_pos/3,y=zero_pos%3;
for(int i=0;i<4;i++){
int x1=x+dir[i][0],y1=y+dir[i][1];
if(x1<0||x1>2||y1<0||y1>2) continue;
int d=m[cur];
swap(cur[x1*3+y1],cur[zero_pos]);
if(!m.count(cur)){
q.push(cur);
m[cur]=d+1;
}
swap(cur[x1*3+y1],cur[zero_pos]);
}
}
}
int main(){
cin>>s;
cout<<BFS();
return 0;
}
//283104765 4
//273645801 15
最短路径
Dijkstra
Dijkstra算法详解 通俗易懂 - 知乎 (zhihu.com)
最短路径—弄懂Dijkstra(迪杰斯特拉)算法 - 云+社区 - 腾讯云 (tencent.com)
Dijkstra 算法是求一个图中一个点到其他所有点的最短路径的算法,
即用来求单源最短路径的。
邻接矩阵版
const int MAXV=1000;//最大顶点数
int n;//顶点数
int G[MAXV][MAXV];
int min_dis[MAXV];//到源点的最短距离
bool vis[MAXV];
void Dijkstra(int s){//s为源点
fill(min_dis,min_dis+MAXV,INF);//初始化min_dis数组为INF
min_dis[s]=0;//源点到自身最短距离为0
for(int i=0;i<n;i++){//循环n次
int u=-1,MIN=INF;
for(int j=0;j<n;j++){//找出未访问的点中距离最短的点
if(!vis[j]&&d[j]<MIN){
u=j;
MIN=d[j];
}
}
//找不到小于INF的d[u],说明剩下的顶点与源点不通
if(u==-1) return;
vis[u]=true;
//更新以u为中介点的点的距离
for(int v=0;v<n;v++){
//如果v未访问,且u能到达v,且以u为中介点更优
if(!vis[u]&&G[u][v]!=INF&&d[u]+G[u][v]<d[v]){
d[v]=d[u]+G[u][v];
}
}
}
}
邻接表+优先队列版
#include<iostream>
#include<stdio.h>
#include<math.h>
#include<algorithm>
#include<string.h>
#include<vector>
#include<time.h>
#include<sstream>
#include<set>
#include<queue>
#include<limits.h>
using namespace std;
#define ll long long
const int INF=0x3f3f3f3f;
const double PI=acos(-1.0);
const double EXP=1E-8;
/*------------------------------------------------------------------------*/
const int MAXV=1000;
struct Edge{//为了邻接表而建
int v,w;//v为边的目标顶点,w为权重
};
struct Node{//为了优先队列而建
int u,dis;//u为顶点编号,dis为到源点的距离
bool operator>(const Node&a) const{
return dis>a.dis;//
}
};
vector<Edge> Adj[MAXV];//图G,Adj[u]存放从顶点u的邻接点
int n,m;//顶点数,边数
int min_dis[MAXV];//到源点的最短距离
bool vis[MAXV];
int pre[MAXV];//pre[v]表示顶点v的最短路径上的前一个点
priority_queue<Node,vector<Node>,greater<Node> > q;
void Dijkstra(int s){
fill(min_dis,min_dis+MAXV,INF);//起始没有选择点
min_dis[s]=0;//从源点开始,到自身距离为0
Node startnode={s,0};
q.push(startnode);
while(!q.empty()){
int u=q.top().u;
q.pop();
if(vis[u])
continue;
vis[u]=true;
//Update the shortest path from neighbor to source
for(vector<Edge>::iterator ed=Adj[u].begin();ed!=Adj[u].end();ed++){
int v=ed->v,w=ed->w;
if(min_dis[v]>min_dis[u]+w){//u到源点的最短距离加上到u的距离比原来到源点的距离更短
min_dis[v]=min_dis[u]+w;
Node next_node={v,min_dis[v]};
q.push(next_node);
pre[v]=u;
}
}
}
}
/*------------------------------------------------------------------------*/
int main(){
clock_t starttime,endtime;
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
/*------------------------------------------------------------------------*/
cin>>n>>m;
/*------------------------------------------------------------------------*/
//starttime=clock();
/*------------------------------------------------------------------------*/
for(int i=0;i<n;i++) pre[i]=i;
for(int i=0;i<m;i++){
int x,y,w;
cin>>x>>y>>w;
Edge e={y,w};
Adj[x].push_back(e);
}
Dijkstra(0);
for(int i=n-1;i>=0;i--) cout<<pre[i]<<" ";
/*------------------------------------------------------------------------*/
//endtime=clock();
//cout<<endl<<(double)(endtime-starttime)/CLOCKS_PER_SEC<<"s";
return 0;
}
拓扑排序
AOV网
一个较大的工程往往被划分成许多子工程,我们把这些子工程称作活动(activity)。在整个工程中,有些子工程(活动)必须在其它有关子工程完成之后才能开始,也就是说,一个子工程的开始是以它的所有前序子工程的结束为先决条件的,但有些子工程没有先决条件,可以安排在任何时间开始。为了形象地反映出整个工程中各个子工程(活动)之间的先后关系,可用一个有向图来表示,图中的顶点代表活动(子工程),图中的有向边代表活动的先后关系,即有向边的起点的活动是终点活动的前序活动,只有当起点活动完成之后,其终点活动才能进行。通常,我们把这种顶点表示活动、边表示活动间先后关系的有向图称做顶点活动网(Activity On Vertex network),简称AOV网。
AOV是一个DAG(有向无环图)。
拓朴排序概念
由某个集合上的一个偏序得到该集合上的一个全序,这个操作称之为拓扑排序。
拓扑排序求法
由AOV网构造拓扑排序的步骤主要是循环执行以下两步,直到不存在入度为0的点为止。
- 寻找一入度为0的点并输出之;
- 删除该点及其所有出边。
拓扑排序用来确定一个依赖关系集中事物发生的顺序。
代码:
用来判断一个图是否是有向无环图
vector<int> G[MAXV];//邻接表
int n,m,inDegree[MAXV];//顶点数、入度
//拓扑排序
bool topologicalSort(){
int num=0; //记录加入拓扑序列的顶点数
queue<int> q;//存储入读为0的点
//将所有入度为0的点压入q
for(int i=0;i<n;i++){
if(inDegree[i]==0){
q.push(i);
}
}
while(!q.empty()){
int u=q.front();
printf("%d ",u);
q.pop();
//将u的邻接点的入度全减1
for(int i=0;i<G(u).size();i++){
int v=G[u][i];
inDegree[v]--;
if(inDegree[v]==0) q.push(v);
}
//清空u的所有出边
G[u].clear();
num++;
}
//加入拓扑序列的顶点数为n,说明拓扑排序成功
if(num==n) return true;
return false;
}
最小生成树
Minimum Spanning Tree,MST
设G=(V,E)是一个无向连通网,生成树上各边的权值之和为该生成树的代价,在G的所有生成树中,代价最小的生成树就称为最小支撑树,或称最小生成树。
只有连通图才有生成树,而对于非连通图,只存在生成森林。
Kruskal 算法
Kruskal 算法是一种常见并且好写的最小生成树算法,由 Kruskal 发明。该算法的基本思想是从小到大加入边,是个贪心算法。
前置知识¶
struct edge{
int u,v;//两个端点编号
int cost;//边权
}E[MAXE];
//按边权从小到大排序
bool cmp(edge a,edge b){
return a.cost<b.cost;
}
int kruskal(){
令最小生成树的边权之和为ans、最小生成树的当前边数Num_Edge;
将所有边按边权从小到大排序;
for(从小到大枚举所有边){
if(当前测试边的两个端点在不同的连通块中){
将该测试边加入最小生成树中;
ans+=测试边的边权;
Num_Edge++;
当Num_Edge=顶点数-1时结束循环;
}
}
return ans;
}
有两个问题:
- 如何判断测试边的两个端点是否在不同的连通块中——并查集的查询功能
- 如何将测试边加入最小生成树——并查集的合并功能
int father[N];//并查集数组
int find(int x){
return father[x]==x?x:fa[x]=find(fa[x]);
}
inline void merge(int x,int y){
fa[find(x)]=find(y);
}
//kruskal函数返回最小生成树的边权之和,参数n为顶点个数,m为图的边数
int kruskal(int n,int m){
//ans为边权之和,Num_Edge为当前生成树的边数
int ans=0,Num_Edge=0;
//并查集初始化
for(int i=1;i<=n;i++){
father[i]=i;
}
//所有边按边权从小到大排序
sort(E,E+m,cmp);
//枚举所有边
for(int i=0;i<m;i++){
int faU=find(E[i].v),faV=find(E[i].u);
//如果不在一个集合中
if(faU!=faV){
//合并集合
father[faU]=faV;
//边权之和增加测试边的边权
ans+=E[i].cost;
//当前生成树的边数+1
Num_Edge++;
//边数等于顶点数减1时结束算法
if(Num_Edge==n-1) break;
}
}
if(Num_Edge!=n-1) return -1;
return ans;
}
蓝桥杯 通电
#include<iostream>
#include<stdio.h>
#include<algorithm>
#include<math.h>
using namespace std;
#define MAXN 1005
typedef long long ll;
struct Village{
int x,y,h;
}V[MAXN];
struct Edge{
int u,v;
double cost;
bool operator<(const Edge&a) const{
return this->cost<a.cost;
}
}E[MAXN*MAXN/2];
int fa[MAXN];
int n;
int m=0;
int find(int x){
return fa[x]==x?x:fa[x]=find(fa[x]);
}
//返回最小生成树的权值
double kruskal(){
for(int i=0;i<n;i++) fa[i]=i;
sort(E,E+m);
double ans=0,Edge_Num=0;
for(int i=0;i<m;i++){
int faU=find(E[i].u),faV=find(E[i].v);
if(faU!=faV){
fa[faU]=faV;
ans+=E[i].cost;
Edge_Num++;
if(Edge_Num==n-1) break;
}
}
if(Edge_Num!=n-1) return -1;
return ans;
}
int main(){
scanf("%d",&n);
int x,y,h;
for(int i=0;i<n;i++) scanf("%d%d%d",&V[i].x,&V[i].y,&V[i].h);
for(int i=0;i<n-1;i++)
for(int j=i+1;j<n;j++)
E[m].cost=sqrt((V[i].x-V[j].x)*(V[i].x-V[j].x)+(V[i].y-V[j].y)*(V[i].y-V[j].y))
+(V[i].h-V[j].h)*(V[i].h-V[j].h),
E[m].u=i,E[m++].v=j;
printf("%f",kruskal());
return 0;
}
数学知识
数论
1 分解质因数
unordered_map<int,int> primes;
void divide(int n){
for(int i=2;i<=n/i;i++){
if(n%i==0){
while(n%i==0){
n/=i;//把质因数i除尽
primes[i]++;//计数该质因数i的个数
}
}
}
if(n>1) primes[n]=1;
}
2 筛质数
2.1 试除法
一次只能判断一个数
bool is_prime(int n){
for(int i=2;i<=n/i;i++)
if(n%i==0) return false;
return true;
}
2.2 埃氏筛
时间复杂度O(nlog(logn))
isprime[0]=isprime[1]=false;
for(int i=2;i<=maxn;i++){
if(isprime[i]){
prime[cnt++]=i;
for(int j=i*i;j<=maxn;j+=i){
isprime[j]=false;
}
}
}
这里有一个小优化,j 从 i * i 而不是从 i + i开始,因为 i*(2~ i-1)在 2~i-1时都已经被筛去,所以从i * i开始。
对于一个合数,有可能被筛多次。例如 30 = 2 * 15 = 3 * 10 = 5*6……
用筛法求之N内的素数。 - C语言网 (dotcpp.com)
2.3 欧拉筛
for(int i=2;i<=maxn;i++){
if(IsPrime[i]) prime[++prime[0]]=i;
for(int j=1;j<=prime[0]&&i*prime[j]<=maxn;j++){
IsPrime[i*prime[j]]=false;
if(i%prime[j]==0) break;
}
}
欧拉筛保证了每个合数只被它的最小质因子筛除。
i
0
%
p
r
i
m
e
[
j
]
=
=
0
保证了这一特性,理由如下,
当
i
0
=
k
∗
p
r
i
m
e
[
j
]
时,
i
0
∗
p
r
i
m
e
[
j
+
1
]
=
p
r
i
m
e
[
j
]
∗
k
∗
p
r
i
m
e
[
j
+
1
]
,
这说明后面当遇到一个
i
1
=
k
∗
p
r
i
m
e
[
j
+
1
]
时,会筛除
i
1
∗
p
r
i
m
e
[
j
]
=
i
0
∗
p
r
i
m
e
[
j
+
1
]
。
\begin{gather*} i_0 \% prime[j]==0保证了这一特性,理由如下,\\ 当i_0=k*prime[j]时,i_0*prime[j+1]=prime[j]*k*prime[j+1],\\ 这说明后面当遇到一个i_1=k*prime[j+1]时,会筛除i_1*prime[j]=i_0*prime[j+1]。\end{gather*}
i0%prime[j]==0保证了这一特性,理由如下,当i0=k∗prime[j]时,i0∗prime[j+1]=prime[j]∗k∗prime[j+1],这说明后面当遇到一个i1=k∗prime[j+1]时,会筛除i1∗prime[j]=i0∗prime[j+1]。
前面的不会筛除后面会筛除的。
例子:求n以内的素数
#include<iostream>
#include<bitset>
using namespace std;
int prime[10000];
bitset<10000> IsPrime;
int main()
{
int n,i,j;
cin >> n;
IsPrime[0] = IsPrime[1] = 1;
for(i=2;i<n;i++){
if(!IsPrime[i]){
prime[++prime[0]] = i;
printf("%d\n", i);
}
for (j = 1; j <= prime[0] && i * prime[j] < n; j++) {
IsPrime[i * prime[j]] = 1;
if (i % prime[j] == 0)
break;
}
}
return 0;
}

#include<stdio.h>
#include<algorithm>
#include<string.h>
#include<sstream>
#include<time.h>
using namespace std;
/*---------------------------------------------------------------*/
#define maxn 20210605
bool IsPrime[maxn];
int prime[maxn];
void oula(){
memset(IsPrime,true,sizeof(IsPrime));
IsPrime[0]=IsPrime[1]=false;
for(int i=2;i<=maxn;i++){
if(IsPrime[i]) prime[++prime[0]]=i;
for(int j=1;j<=prime[0]&&i*prime[j]<=maxn;j++){
IsPrime[i*prime[j]]=false;
if(i%prime[j]==0) break;
}
}
}
bool judge(int x){
if(!IsPrime[x]) return false;
while(x!=0){
if(!IsPrime[x%10]) return false;
x/=10;
}
return true;
}
int ans;
/*---------------------------------------------------------------*/
int main(){
clock_t starttime,endtime;
starttime=clock();
/*---------------------------------------------------------------*/
oula();
for(int i=1;i<=maxn;i++){
if(judge(i)){
printf("%d ",i);
ans++;
}
}
printf("%d",ans);
/*---------------------------------------------------------------*/
endtime=clock();
printf("\n耗时:%f s\n",(double)(endtime-starttime)/CLOCKS_PER_SEC);
return 0;
}
2.4 杜教筛
2.5 min_25筛
3 约数
3.1 试除法求约数
https://www.acwing.com/problem/content/871/
vector<int> get_divisors(int x)
{
vector<int> res;
for (int i = 1; i <= x / i; i ++ )
if (x % i == 0)
{
res.push_back(i);
if (i != x / i) res.push_back(x / i);
}
sort(res.begin(), res.end());
return res;
}
auto res=get_divisors(n);
for(auto t:res) cout<<t<<' ';
3.2 约数个数和约数之和
如果 N = p 1 c 1 × p 2 c 2 × . . . × p k c k 约数个数: ( c 1 + 1 ) × ( c 2 + 1 ) × . . . × ( c k + 1 ) 约数之和: ( p 1 0 + p 1 1 + . . . + p 1 c 1 ) × . . . × ( p k 0 + p k 1 + . . . + p k c k ) \begin{gather*}如果\space N ={p_1}^{c_1}\times{p_2}^{c_2}\times...\times{p_k}^{c_k}\\ 约数个数:(c_1+1)\times(c_2+1)\times...\times(c_k+1)\\ 约数之和:({p_1}^{0}+{p_1}^{1}+...+{p_1}^{c_1})\times...\times({p_k}^{0}+{p_k}^{1}+...+{p_k}^{c_k})\end{gather*} 如果 N=p1c1×p2c2×...×pkck约数个数:(c1+1)×(c2+1)×...×(ck+1)约数之和:(p10+p11+...+p1c1)×...×(pk0+pk1+...+pkck)
求约数个数
#include<iostream>
#include<algorithm>
#include<unordered_map>
using namespace std;
typedef long long ll;
const int mod=1e9+7;
int main(){
int n;
cin>>n;
unordered_map<int,int> primes;
while(n--){
int x;
cin>>x;
for(int i=2;i<=x/i;i++){
while(x%i==0){
x/=i,primes[i]++;
}
}
if(x>1) primes[x]++;
}
ll res=1;
for(auto prime:primes) res*=(prime.second+1)%mod;
cout<<res;
return 0;
}
约数和
#include<iostream>
#include<algorithm>
#include<unordered_map>
using namespace std;
typedef long long ll;
const int mod=1e9+7;
int main(){
int n;
cin>>n;
unordered_map<int,int> primes;
while(n--){
int x;
cin>>x;
for(int i=2;i<=x/i;i++){
while(x%i==0){
x/=i,primes[i]++;
}
}
if(x>1) primes[x]++;
}
ll res=1;
for(auto prime:primes){
int p=prime.first,a=prime.second;
ll t=1;
while(a--) t=(t*p+1)%mod;
res*=(t%mod);
}
cout<<res;
return 0;
}
线性筛求约数个数
void pre(){
d[1]=1;
for(int i=2;i<=n;i++){
if(!v[i]) v[i]=1,p[++tot]=i,d[i]=2,num[i]=1;
for(int j=1;j<=tot&&i<=n/p[j];++j){
v[i*p[j]]=1;
if(i%p[j]==0){
num[i*p[j]]=num[i]+1;
d[i*p[j]]=d[i]/num[i*p[j]]*(num[i*p[j]]+1);
break;
}else{
num[i*p[j]]=1;
d[i*p[j]]=d[i]*2;
}
}
}
}
线性筛求约数和
3.3 最大公约数-欧几里得算法
gcd(a,b)=gcd(b,a mod b);
int gcd(int a,int b){ return b==0?a:gcd(b,a%b); }
int gcd(int a,int b){while(b^=a^=b^=a%=b);return a;}
4 欧拉函数
#欧拉函数
欧拉函数
φ
(
n
)
\varphi (n)
φ(n)表示小于等于n且和n互质(gcd=1)的数的数量。
φ
(
1
)
=
1
\varphi(1)=1
φ(1)=1。
当n是质数的时候,显然有
φ
(
n
)
=
n
−
1
\varphi(n)=n-1
φ(n)=n−1。
欧拉函数的一些性质
- 欧拉函数是积性函数。
- 积性是指对于两个互质的整数a和b有f(ab)=f(a) × \times ×f(b)。
- 特别地对于n是奇数时, φ ( 2 n ) = φ ( n ) \varphi(2n)=\varphi(n) φ(2n)=φ(n)。
- n= ∑ d ∣ n φ ( d ) \sum_{d|n}{\varphi(d)} ∑d∣nφ(d)。
- 若 n = p k n=p^k n=pk,其中p是质数,那么 φ ( n ) = p k − p ( k − 1 ) \varphi(n)=p^k-p^(k-1) φ(n)=pk−p(k−1)。
- 根据整数唯一分解定理(算术基本定理),设
φ
(
n
)
=
n
×
∏
i
=
1
s
p
i
−
1
p
i
\varphi (n)=n\times \prod_{i=1}^{s}{\frac{p_i-1}{p_i}}
φ(n)=n×∏i=1spipi−1.
![[Pasted image 20220524150902.png]]
如何求欧拉函数值
求一个数的欧拉函数值
根据定义质因数分解的同时求解就好。这个过程可以用Pollard Rho算法优化。
int euler_phi(int n){
int m=int(sqrt(n+0.5));
int ans=n;
for(int i=2;i<=m;i++)
if(n%i==0){
ans=ans/i*(i-1);
while(n%i==0) n/=i;
}
if(n>1) ans=ans/n*(n-1);
return ans;
}
优化
int euler_phi(int n){
int ans=n;
for(int i=2;i<=n/i;i++)
if(n%i==0){
ans=ans/i*(1-i);
while(n%i==0) n/=i;
}
if(n>1) ans=ans/n*(n-1);
return ans;
}
求多个数的欧拉函数值
线性筛(euler筛)求解欧拉函数

void pre(){
memset(is_prime,1,sizeof is_prime);
int cnt=0;
is_prime[1]=0;
phi[i]=1;
for(int i=2;i<=5000000;i++){
if(is_prime[i]){
prime[++cnt]=i;
phi[i]=i-1;
}
for(int j=1;j<=cnt&&i*prime[j]<=5000000;j++){
is_prime[i*prime[j]]=0;
if(i%prime[j])
phi[i*prime[j]]=phi[i]*phi[prime[j]];
else{
phi[i*prime[j]]=phi[i]*prime[j];
break;
}
}
}
}
欧拉定理
若 g c d ( a , m ) = 1 ,则 a φ ( m ) ≡ 1 ( m o d m ) gcd(a,m)=1,则a^{\varphi (m)}\equiv1(\mod m) gcd(a,m)=1,则aφ(m)≡1(modm)。
当m为质数时,欧拉定理变为了费马定理,
此时
φ
(
m
)
=
m
−
1
\varphi (m)=m-1
φ(m)=m−1,则费马定理内容为,
若
g
c
d
(
a
,
m
)
=
1
,则
a
m
−
1
≡
1
(
m
o
d
m
)
gcd(a,m)=1,则a^{m-1}\equiv1(\mod m)
gcd(a,m)=1,则am−1≡1(modm)。
扩展欧拉定理
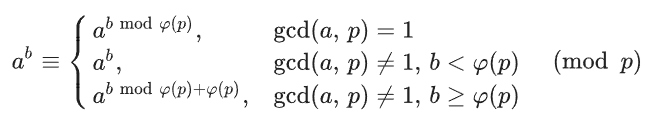
5 快速幂
#快速幂
a
b
a^b
ab
long long binpow(long long a,long long b){
long long res=1;
while(b>0){
if(b&1) res*=a;
a*=a;
b>>1;
}
return res;
}
a b % m a^b \% m ab%m
long long binpow(long long a,long long b,long long m){
long long res =1;
while(b>0){
if(b&1) res=res*a%m;
a=a*a%m;
b>>1;
}
return res%m;
}
矩阵快速幂
快速幂求乘法逆元
乘法逆元
若gcd(b,m)=1,b|a,则
a
b
≡
a
˙
b
−
1
(
m
o
d
m
)
\frac{a}{b}\equiv a \dot \ b^{-1}(\mod m)
ba≡a ˙b−1(modm)
把除法变为乘法。
上式两边同乘b得
a
≡
a
˙
b
˙
b
−
1
(
m
o
d
m
)
。
a \equiv a \dot \ b \dot \ b^{-1}(\mod m)。
a≡a ˙b ˙b−1(modm)。
两边同除以a得
b
˙
b
−
1
≡
1
(
m
o
d
m
)
b \dot \ b^{-1} \equiv 1(\mod m)
b ˙b−1≡1(modm)
6 扩展欧几里得
#include<stdio.h>
int exgcd(int a,int b,int &x,int &y){
if(!b){
x=1;y=0;
return a;
}
int d=exgcd(b,a%b,y,x);
y-=(a/b)*x;
return d;
}
int main(){
int x,y;
exgcd(2,3,x,y);
printf("%d %d",x,y);
return 0;
}
7 中国剩余定理
中国剩余定理 (Chinese Remainder Theorem, CRT) 可求解如下形式的一元线性同余方程组,其中
{
n
1
,
n
2
,
.
.
.
,
n
k
两两互质
}
\{n_1,n_2,... ,n_k两两互质\}
{n1,n2,...,nk两两互质}
{
x
≡
a
1
(
m
o
d
n
1
)
x
≡
a
2
(
m
o
d
n
2
)
.
.
.
x
≡
a
k
(
m
o
d
n
k
)
\begin{cases} & x \equiv a_{1}(\mod n_1) \\ & x \equiv a_{2}(\mod n_2) \\ & . \\ & . \\ & . \\ & x \equiv a_{k}(\mod n_k) \end{cases}
⎩
⎨
⎧x≡a1(modn1)x≡a2(modn2)...x≡ak(modnk)
算法流程
- 计算所有模数的积n;
- 对于第i个方程:
a.计算 m i = n n i m_i=\frac{n}{n_i} mi=nin;
b.计算 m i m_i mi在 n i n_i ni意义下的逆元 m i − 1 {m_i}^{-1} mi−1;
c.计算 c i = m i m i − 1 c_i=m_im_i^{-1} ci=mimi−1(不要对 n i n_i ni取模)。 - 方程组的唯一解为: x = ∑ i = 1 k a i c i ( m o d n ) x=\sum_{i=1}^{k}{a_ic_i(\mod n)} x=∑i=1kaici(modn)。
LL CRT(int k,LL* a,LL *r){
LL n=1,,ans=0;
for(int i=1;i<=k;i++) n*=r[i];//计算所有模数的积n
for(int i=1;i<=k;i++){
LL m=n/r[i],b,y;
exgcd(m,r[i],b,y);//b*m mod r[i]=1
ans=(ans+a[i]*m*b%n)%n;
}
return (ans%n+n)%n;
}
8 裴蜀定理
对于任意正整数a,b一定存在整数x,y,使得ax+by=gcd(a,b)。
可应用扩展欧几里得来算出这样的一组(x,y)。
字符串
数据结构
并查集
算法学习笔记(1) : 并查集 - 知乎 (zhihu.com)
初始化

int fa[MAXN];
inline void init(int n)
{
for (int i = 1; i <= n; ++i)
fa[i] = i;//父节点为自己
}
查询
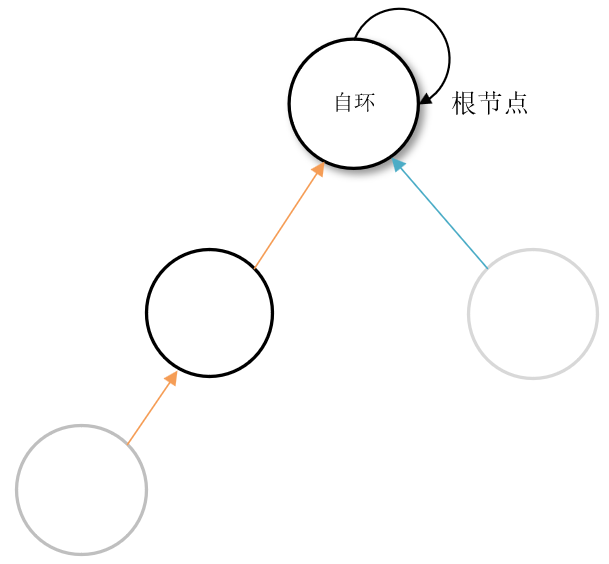
一层一层访问父节点,直至根节点(根节点的标志就是父节点是本身)。要判断两个元素是否属于同一个集合,只需要看它们的根节点是否相同即可。
int find(int x)
{
if(fa[x] == x)//父节点为自身,为根节点
return x;
else
return find(fa[x]);
}
合并
inline void merge(int i, int j)
{
fa[find(i)] = find(j);//把i的父节点的父节点设置为j的父节点
}
查询(路径压缩)
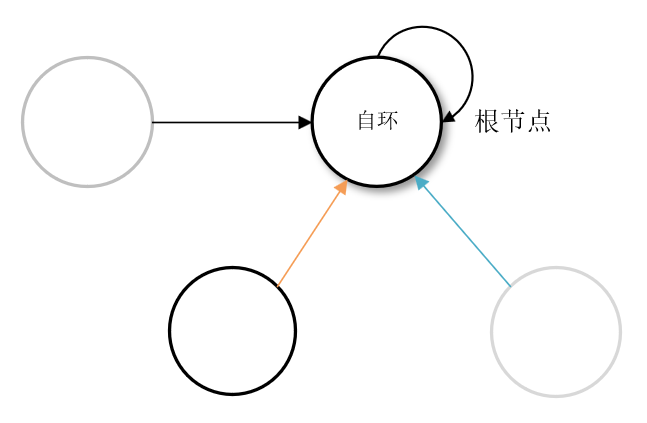
int find(int x)
{
if(x == fa[x])
return x;
else{
fa[x] = find(fa[x]); //父节点设为父节点的父节点,最后这条路上所有点父节点都设为根节点
return fa[x]; //返回父节点
}
}
以上代码常常简写为一行:
int find(int x)
{
return x == fa[x] ? x : (fa[x] = find(fa[x]));
}
初始化(按秩合并)
inline void init(int n)
{
for (int i = 1; i <= n; ++i)
{
fa[i] = i;
rank[i] = 1;
}
}
合并(按秩合并)
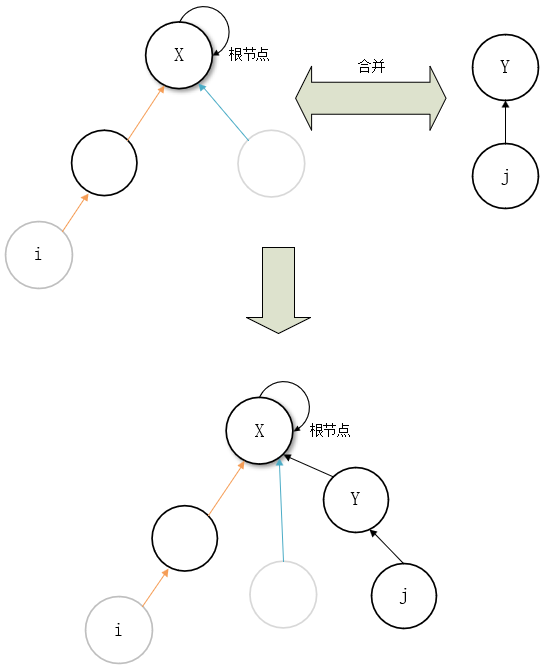
inline void merge(int i, int j)
{
int x = find(i), y = find(j); //先找到两个根节点
if (rank[x] <= rank[y])//x的高度小于等于y,则合并x那一路到y
fa[x] = y;
else
fa[y] = x;
if (rank[x] == rank[y] && x != y)//如果高度相同且根节点不同,则新的根节点的高度+1
rank[y]++;
}
线段树
基本操作:
①pushup():由子节点算父节点
②build():将一段区间初始化为线段树,若区间长度为n,则存储线段树的一维空间长度建议为4*n。
③modify():修改,分为对单点的修改和对区间的修改,其中对区间修改涉及pushdown()操作函数和懒标记。
④query():查询某段区间
对于编号为x的结点:其父节点为x>>1,左儿子为x<<1,右儿子为x<<1|1。
单点修改
区间最大值查询
struct Node{
int l,r;
int v;
}tr[MAXN*4];
void build(int u,int l,int r){
if(l==r) {
tr[u]={l,r};
return;
}
int mid=l+r>>1;
build(u<<1,l,mid),build(u<<1|1,mid+1,r);
pushup(u);
}
void pushup(int u){
tr[u]=max(tr[u<<1],tr[u<<1|1]);
}
int query(int u,int l,int r){
if(tr[u].l>=l&&tr[u].r<=r) return tr[u].v;
int mid=tr[u].l+tr[u].r>>1;
int v=0;
if(l<=mid) v=query(u<<1,l,r);
else v=max(v,query(u<<1|1,l,r));
return v;
}
void modify(int u,int x,int v){
if(tr[u].l==x&&tr[u].r==x) tr[u].v=v;
else{
int mid=tr[u].l+tr[u].r>>1;
if(x<=mid) modify(u<<1,x,v);
else modify(u<<1|1,x,v);
pushup(u);
}
}
区间最大连续子段和查询
int w[MAXN];//数列
struct Node{
int l,r;
int sum,lmax,rmax,tmax;
}tr[MAXN*4];
void pushup(Node &u,Node &l,Node &r){
u.sum=l.sum+r.sum;
u.lmax=max(l.lmax,l.sum+r.lmax);
u.rmax=max(r.rmax,r.sum+l.rmax);
u.tmax=max(max(l.tmax,r.tmax),l.rmax+r.lmax);
}
void pushup(int u){
pushup(tr[u],tr[u<<1],tr[u<<1|1]);
}
void build(int u=1,int l=1,int r=n){
if(l==r) tr[u]={l,r,w[r],w[r],w[r],w[r]};
else{
int mid=tr[u].l+tr[u].r>>1;
build(u<<1,l,mid),build(u<<1|1,mid+1,r);
pushup(u);
}
}
int modify(int u=1,int x,int v){
if(tr[u].l==x&&tr[u].r==x) tr[u]={x,x,v,v,v};
else{
int mid=tr[u].l+tr[u].r>>1;
if(l<=mid) modify(u<<1,x,v);
else modify(u<<1|1,x,v);
pushup(u);
}
}
Node query(int u=1,int l,int r){
if(tr[u].l>=l&&tr[u].r<=r) return tr[u];
else{
int mid=tr[u].l+tr[u].r>>1;
if(r<=mid) return query(u<<1,l,r);
else if(l>mid) return query(u<<1|1,l,r);
else{
auto left=query(u<<1,l,r);
auto right=query(u<<1|1,l,r);
Node res;
pushup(res,left,right);
return res;
}
}
}
求Max和Sum
#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
const int MAXN=510;
int n,m;
int w[MAXN];
struct Node{
int l,r;
int v;
int sum;
}tr[MAXN*4];
void pushup(int u){
tr[u].v=max(tr[u<<1].v,tr[u<<1|1].v);
tr[u].sum=tr[u<<1].sum+tr[u<<1|1].sum;
}
void build(int u,int l,int r){
if(l==r) tr[u]={l,r,w[l],w[l]};
else{
int mid=l+r>>1;
tr[u]={l,r};
build(u<<1,l,mid),build(u<<1|1,mid+1,r);
pushup(u);
}
}
int modify(int u,int x,int v){
if(tr[u].l==x&&tr[u].r==x) tr[u].v=v;
else{
int mid=tr[u].l+tr[u].r>>1;
if(x<=mid) modify(u<<1,x,v);
else modify(u<<1|1,x,v);
pushup(u);
}
}
int queryMax(int u,int l,int r){
if(tr[u].l>=l&&tr[u].r<=r) return tr[u].v;
else{
int mid=tr[u].l+tr[u].r>>1;
int v=0;
if(l<=mid) v = queryMax(u<<1,l,r);
else v=max(v,queryMax(u<<1|1,l,r));
return v;
}
}
int querySum(int u,int l,int r){
if(tr[u].l==l&&tr[u].r==r) return tr[u].sum;
else{
int mid=tr[u].l+tr[u].r>>1;
if(r<=mid) return querySum(u<<1,l,r);
else if(l>mid) return querySum(u<<1|1,l,r);
else return querySum(u<<1,l,mid)+querySum(u<<1|1,mid+1,r);
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&w[i]);
build(1,1,n);
while(m--){
int p,x,y;
scanf("%d%d%d",&p,&x,&y);
if(p==1) modify(1,x,y);
else if(p==2) printf("Max=%d\n",queryMax(1,x,y));
else printf("Sum=%d\n",querySum(1,x,y));
}
return 0;
}
/*
5 2
1 2 3 4 5
2 1 3
3 1 3
*/
蓝桥杯 操作格子
https://buctcoder.com/problem.php?id=3178
#include<stdio.h>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
const int MAXN=100010;
int n,m;
int w[MAXN];
struct Node{
int l,r;
int v;
int sum;
}tr[MAXN*4];
void pushup(int u){
tr[u].v=max(tr[u<<1].v,tr[u<<1|1].v);
tr[u].sum=tr[u<<1].sum+tr[u<<1|1].sum;
}
void build(int u,int l,int r){
if(l==r) tr[u]={l,r,w[l],w[l]};
else{
int mid=l+r>>1;
tr[u]={l,r};
build(u<<1,l,mid),build(u<<1|1,mid+1,r);
pushup(u);
}
}
void modify(int u,int x,int v){
if(tr[u].l==x&&tr[u].r==x) tr[u].v=v,tr[u].sum=v;
else{
int mid=tr[u].l+tr[u].r>>1;
if(x<=mid) modify(u<<1,x,v);
else modify(u<<1|1,x,v);
pushup(u);
}
}
int queryMax(int u,int l,int r){
if(tr[u].l>=l&&tr[u].r<=r) return tr[u].v;
else{
int mid=tr[u].l+tr[u].r>>1;
if(r<=mid) return queryMax(u<<1,l,r);
else if(l>mid) return queryMax(u<<1|1,l,r);
else return max(queryMax(u<<1,l,mid),queryMax(u<<1|1,mid+1,r));
}
}
ll querySum(int u,int l,int r){
if(tr[u].l==l&&tr[u].r==r) return tr[u].sum;
else{
int mid=tr[u].l+tr[u].r>>1;
if(r<=mid) return querySum(u<<1,l,r);
else if(l>mid) return querySum(u<<1|1,l,r);
else return querySum(u<<1,l,mid)+querySum(u<<1|1,mid+1,r);
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&w[i]);
build(1,1,n);
while(m--){
int p,x,y;
scanf("%d%d%d",&p,&x,&y);
if(p==1) modify(1,x,y);
else if(p==3) printf("%d\n",queryMax(1,x,y));
else printf("%lld\n",querySum(1,x,y));
}
return 0;
}
奇怪的宇宙
https://buctcoder.com/problem.php?cid=2614&pid=0
线段树DFS序列空间优化+__int128防爆
线段树结点k,左孩子为k+1,
若 right-left 是偶数,sizeof(左孩子) = right-left+1; (故右孩子为 k+right-left+2)
若 right-left 是奇数,sizeof(左孩子) = right-left; (故右孩子为 k+right-left+1)
#include<stdio.h>
#include<math.h>
#include<algorithm>
#include<vector>
#include<stack>
using namespace std;
const int MAXN=500010;
int w[MAXN];
struct Node{
int v;//最大值
int q;//最大值数量
}tr[MAXN*2-1];
void pushup(Node &u,Node &l,Node &r){
u.v=max(l.v,r.v);
if(l.v==r.v)
u.q=l.q+r.q;
else u.q=(l.v>r.v?l.q:r.q);
}
void pushup(int u,int lu,int ru){
pushup(tr[u],tr[lu],tr[ru]);
}
void build(int u,int l,int r){
if(l==r) tr[u]={w[l],1};
else{
int mid = l + r >> 1;
int lu=u+1,ru=r-l&1?u+1+r-l:u+2+r-l;
build(lu,l,mid),build(ru,mid+1,r);
pushup(u,lu,ru);
}
}
Node query(int u,int l,int r,int cl,int cr){
if(l<=cl&&cr<=r) return tr[u];
else{
int mid=cl+cr>>1;
int lu=u+1,ru=r-l&1?u+1+r-l:u+2+r-l;
if(r<=mid) return query(lu,l,r,cl,mid);
else if(l>mid) return query(ru,l,r,mid+1,cr);
else{
Node left=query(lu,l,r,cl,mid);
Node right=query(ru,l,r,mid+1,cr);
Node res;
pushup(res,left,right);
return res;
}
}
}
void print(__int128 x){
stack<int>s;
while(x){
s.push(x%10);
x /= 10;
}
while(!s.empty()){
printf("%d",s.top());
s.pop();
}
}
__int128 sum;
int main(){
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&w[i]);
int l,r;
build(1,1,n);
while(m--){
scanf("%d%d",&l,&r);
if(l>r) swap(l,r);
Node t=query(1,l,r,1,n);
sum+=t.v*1ll*t.q;
}
print(sum);
return 0;
}
动态规划
动态规划(Dynamic Programming ,DP)是一种解决一类最优化问题的思想。
简单地来说,DP将一个复杂的问题分解成若干个子问题,通过综合子问题的最优解来得到原问题的最优解。
需要注意的是,DP会将每个求解过的子问题的解记录下来,这样当下一次碰到同样的子问题时,就可以直接使用之前记录的结果,而不是重复计算。
注意:虽然动态规划采用这种方式来提高计算效率,但不能说这种做法就是DP的核心。
一般可以使用递归或递推的写法来实现动态规划,其中递归写法在此处又称作记忆化搜索。
斐波那契数列
数塔问题
最大连续子序列和
给定一个数字序列 A 1 , A 2 , . . . , A n A_1,A_2,...,A_n A1,A2,...,An,求i,j(1<=i<=j<=n),使得 A i + . . . + A j A_i+...+A_j Ai+...+Aj最大输出这个最大和。
dp[i]表示以A[i]结尾的连续序列的和。
d
p
[
i
]
=
m
a
x
(
A
[
i
]
,
d
p
[
i
−
1
]
+
A
[
i
]
)
dp[i]=max(A[i],dp[i-1]+A[i])
dp[i]=max(A[i],dp[i−1]+A[i])
我们必须设计一个拥有无后效性的状态以及相应的状态转移方程,否则动态规划就没有办法得到正确结果。
事实上,如何设计状态和状态转移方程,才是动态规划的核心,而它们也是动态规划最难的地方。
最长不下降子序列(LIS)
在一个数字序列中,找到一个最长的不下降子序列。
dp[i]表示一个以A[i]结尾的LIS。
int ans=-1;
for(int i=1;i<=n;i++){
dp[i]=1;
for(int j=1;j<i;j++){
if(A[i]>=A[j]&&dp[j]+1>dp[i]){
dp[i]=dp[j]+1;
}
ans=max(ans,dp[i]);
}
}
最长公共子序列(LCS)
给定两个字符串(或数字序列)A和B,求一个字符串,使得这个字符串是A和B的最长公共部分(子序列可以不连续)。
dp[i][j]表示字符串A的i号位和j号位之前的LCS长度(下标从1开始)。
分两种决策,
①A[i]=B[j],dp[i][j]=dp[i-1][j-1]+1。
②A[i]!=B[j],dp[i][j]=max{dp[i-1][j],dp[i][j-1]}。
最长回文子串
给出一个字符串S,求S的最长回文子串的长度。
dp[i][j]表示从S[i]-S[j]是否为回文串。
int main(){
gets(S);
int len=strlen(S),ans=1;
memset(dp,0,sizeof dp);
//边界
for(int i=0;i<len;i++){
dp[i][i]=1;
if(i<len-1){
if(S[i]==s[i+1]){
dp[i][i+1]=1;
ans=2;
}
}
}
//状态转移方程
for(int L=3;L<=len;L++){
for(int i=0;i+L-1<len;i++){
int j=i+L-1;
if(S[i]==S[j]&&dp[i+1][j-1]){
dp[i][j]=1,ans=L;
}
}
}
}
背包问题
01背包问题
有n件物品,每件物品的重量为w[i],价值为c[i]。现有一个容量为V的背包,问如何选取物品放入背包,使得背包内物品的总价值最大。其中每种物品都只有1件。
dp[i][v]表示前i件物品恰好装入容量为v的背包中所能获得的最大价值
考虑对第i件物品的选择策略,
①不放第i件物品,那么问题转化为前i-1恰好装入容量为v的背包中所能获得的最大价值,即dp[i-1][v]。
②放第i件物品,那么问题转化为前i-1件物品恰好装入容量为v-w[i]的背包中所能获得的最大价值,即dp[i-1][v-w[i]]+c[i]
d
p
[
i
]
[
v
]
=
m
a
x
(
d
p
[
i
−
1
]
[
v
]
,
d
p
[
i
−
1
]
[
v
−
w
[
i
]
]
+
c
[
i
]
)
dp[i][v]=max(dp[i-1][v],dp[i-1][v-w[i]]+c[i])
dp[i][v]=max(dp[i−1][v],dp[i−1][v−w[i]]+c[i])
for(int i=1;i<=n;i++){
for(int v=w[i];v<=V;v++){
dp[i][v]=max(dp[i-1][v],dp[i-1][v-w[i]]+c[i]);
}
}
空间优化,开一个一维数组dp[v],枚举方向v从V到0。
for(int i=1;i<=n;i++){
for(int v=V;v>=w[i];v--){
dp[v]=max(dp[v],dp[v-w[i]]+c[i]);
}
}
完全背包问题
有n件物品,每件物品的重量为w[i],价值为c[i]。现有一个容量为V的背包,问如何选取物品放入背包,使得背包内物品的总价值最大。其中每种物品有无穷件。
d
p
[
i
]
[
v
]
=
m
a
x
(
d
p
[
i
−
1
]
[
v
]
,
d
p
[
i
]
[
v
−
w
[
i
]
]
+
c
[
i
]
)
dp[i][v]=max(dp[i-1][v],dp[i][v-w[i]]+c[i])
dp[i][v]=max(dp[i−1][v],dp[i][v−w[i]]+c[i])
d p [ v ] = m a x ( d p [ v ] , d p [ v − w [ i ] ] + c [ i ] ) dp[v]=max(dp[v],dp[v-w[i]]+c[i]) dp[v]=max(dp[v],dp[v−w[i]]+c[i])
for(int i=1;i<=n;i++){
for(int v=w[i];v<=V;v--){
dp[v]=max(dp[v],dp[v-w[i]]+c[i]);
}
}
树形dp
没有上司的舞会
dfs+树形dp
#include<bits/stdc++.h>
using namespace std;
#define MAXN 6005
int h[MAXN];//快乐指数
bool v[MAXN];//是否已访问
vector<int> Adj[MAXN];//邻接表
int f[MAXN][2];
/*
对每个职员有去或不去两种决策
f[x][0]表示以x为根且x不去参加舞会的最大快乐值
f[x][1]表示以x为根且x去参加舞会的最大快乐值
*/
void dfs(int x) {
f[x][0]=0;
f[x][1]=h[x];
for(auto i:Adj[x]) {
int y=i;
dp(y);
f[x][0]+=max(f[y][0],f[y][1]);//加上所有儿子结点最优决策的和
f[x][1]+=f[y][0];//再加上孙子节点参加增加的快乐值
}
}
int main() {
int n;//职员数
cin>>n;
for(int i=1; i<=n; i++) cin>>h[i];
for(int i=1; i<=n-1; i++) {
int x,y;//y是x的上司
cin>>x>>y;
Adj[y].push_back(x);
v[x]=true;
}
int root;
//找到根结点,最顶级的上司
for(int i=1; i<=n; i++)
if(!v[i]) {
root=i;
break;
}
dfs(root);
cout<<max(f[root][0],f[root][1])<<endl;
return 0;
}
最小权值

#include<stdio.h>
#include<algorithm>
#include<string.h>
#include<sstream>
#include<time.h>
#include<math.h>
using namespace std;
#define ll long long
#define INF 0x3f3f3f3f3f3f
/*---------------------------------------------------------------*/
#define maxn 2050
ll dp[maxn];//dp[i]表示有i个节点的树的权值。
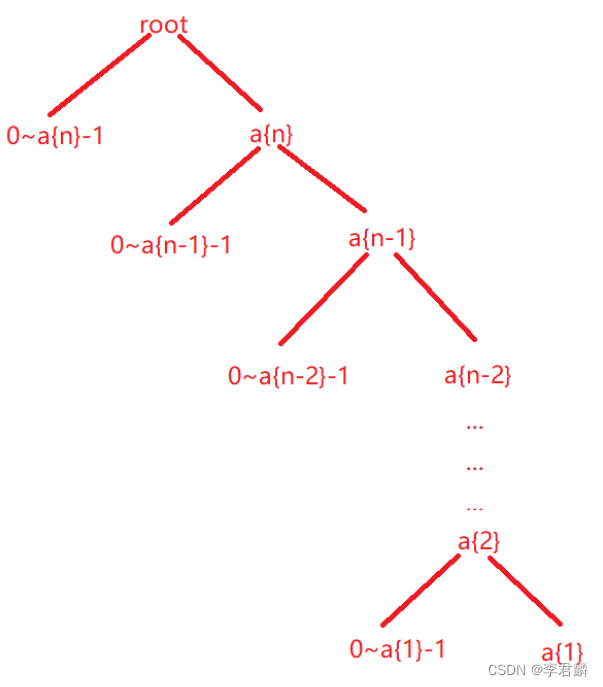
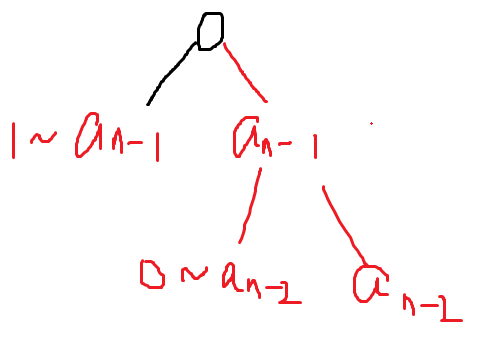
ll dfs(int n){
if(dp[n]!=INF) return dp[n];
for(int i=0;i<n;i++){//左子树有0个结点到i-1个结点
dp[n]=min(dp[n],1+2*dfs(i)+3*dfs(n-i-1)+i*i*(n-i-1));
}
return dp[n];
}
/*---------------------------------------------------------------*/
int main(){
clock_t starttime,endtime;
starttime=clock();
/*---------------------------------------------------------------*/
for(int i=1;i<=2021;i++) dp[i]=INF;
ll ans=dfs(2021);
printf("%lld",ans);
/*---------------------------------------------------------------*/
endtime=clock();
printf("\n耗时:%f s\n",(double)(endtime-starttime)/CLOCKS_PER_SEC);
return 0;
}
数位DP
数位DP关注数的每一位上的数字。
数位DP用来解决一类特定类型的问题,他们有如下特征:
- 要求统计满足
一定条件的数的数量; - 这些条件
经过转化后可以使用【数位】的思想去理解和判断; - 输入会提供
一个数字区间(有时也只提供上界)来作为统计的限制; - 上界很大(比如
1
0
18
10^{18}
1018),
暴力枚举验证会超时。
数位DP的基本原理:
考虑人类计数的方式,最朴素的计数就是从小到大开始依次加一。但我们发现对于位数比较多的数,这样的过程中有许多重复的部分。例如,从 7000 数到 7999、从 8000 数到 8999、和从 9000 数到 9999 的过程非常相似,它们都是后三位从 000 变到 999,不一样的地方只有千位这一位,所以我们可以把这些过程归并起来,将这些过程中产生的计数答案也都存在一个通用的数组里。此数组根据题目具体要求设置状态,用递推或 DP 的方式进行状态转移。
数位 DP 中通常会利用常规计数问题技巧,比如把一个区间内的答案拆成两部分相减,即
a
n
s
[
l
,
r
]
=
a
n
s
[
0
,
r
]
−
a
n
s
[
0
,
l
−
1
]
ans[l,r]=ans[0,r]-ans[0,l-1]
ans[l,r]=ans[0,r]−ans[0,l−1]
那么有了通用答案数组,接下来就是统计答案。统计答案可以选择记忆化搜索,也可以选择循环迭代递推。为了不重不漏地统计所有不超过上限的答案,要从高到低枚举每一位,再考虑每一位都可以填哪些数字,最后利用通用答案数组统计答案。
例题
✏️例1 Luogu P2602数字计数
题目大意:给定两个正整数a,b,求在[a,b]中的所有整数中,每个数码(digit)各出现了多少次。
方法一
对于i位数,他们组成的集合里所有数字出现的次数是相同的。
故设
d
p
i
dp_i
dpi为i位数的每个数字出现的次数(都是相同的就用一个表示),此时暂时不处理前导零。
则有 d p i = 10 × d p i − 1 + 1 0 i − 1 dp_i=10\times dp_{i-1}+10^{i-1} dpi=10×dpi−1+10i−1,这两部分前一个是来自前i-1位数字的贡献,后一个是来自第i位数字的贡献。
有了dp数组,我们来考虑如何统计答案。将上界按位分开,从高到低枚举,不贴着上界时,后面可以随便取值;贴着上界时,后面就只能取0到上界。分两部分分别计算贡献。最后考虑前导零,第i位为前导0时,此时1到i-1位也都是0,也就是多算了将i-1位填满的答案,需要额外减去。
#include<bits/stdc++.h>
using namespace std;
const int N=15;
typedef long long ll;
//dp[i]表示i位数的每一位数字出现次数,sum[i]表示,mi[i]即幂,10^(i-1)。
ll l,r,dp[N],mi[N];
//ans1[N]记录右边界的每一位数字的情况,ans[2N]记录左边界的每一位数字的情况。
ll ans1[N],ans2[N];
//从低到高存储每一位
int a[N];
inline void solve(ll n,ll *ans){
ll tem=n;
//位数长度
int len=0;
//预处理a数组
while(n) a[++len]=n%10,n/=10;
//从高到低处理
for(int i=len;i>=1;--i){
//上界等于a[i]时,a[i]为1-9
for(int j=0;j<10;j++) ans[j]+=dp[i-1]*a[i];
//a[i]为0时的情况数
tmp-=mi[i-1]*a[i],ans[a[i]]+=tmp+1;
//上界小于a[i]时
for(int j=0;j<a[i];j++) ans[j]+=mi[i-1];
//减去前导零
ans[0]-=mi[i-1];
}
}
int main(){
scanf("%lld%lld",&l,&r);
mi[0]=1ll;
//预处理dp数组,dp[i]=dp[i-1]*10+10^(i-1)
for(int i=1;i<=13;++i){
dp[i]=dp[i-1]*10+mi[i-1];
mi[i]=10ll*mi[i-1];
}
//计算ans1,ans2
solve(r,ans1),solve(l-1,ans2);
for(int i=0;i<10;++i) printf("%lld",ans1[i]-ans2[i]);
return 0;
}
二进制问题
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<vector>
using namespace std;
using ll=long long;
const ll MAXN=100;
ll N,K;
ll dp[MAXN][MAXN];
void init(){
for(int i=0;i<=MAXN;i++){
for(int j=0;j<=i;j++){
if(!j) dp[i][j]=1;
else dp[i][j]=dp[i-1][j-1]+dp[i-1][j];
}
}
}
ll solve(ll n){
if(!n) return 0;
vector<int> nums;
while(n) nums.push_back(n&1),n>>=1;
ll res=0;
ll last=0;
for(int i=nums.size()-1;i>=0;i--){
int x=nums[i];
if(x){
res+=dp[i][K-last];
last++;
if(last>K) break;
}
if(!i&&last==K) res++;
}
return res;
}
int main(){
scanf("%lld%lld",&N,&K);
init();
printf("%lld",solve(N));
return 0;
}
度的数量

C
a
b
=
C
a
−
1
b
−
1
+
C
a
−
1
b
C_{a}^{b}=C_{a-1}^{b-1}+C_{a-1}^{b}
Cab=Ca−1b−1+Ca−1b
问题本质上是求解组合数
例如X=10,Y=15,当K=2,B=2时,是求[1,10]之间的十进制数的二进制表示包含两位1的数量。
1 0 10 = 101 0 2 10_{10}=1010_{2} 1010=10102,
①从高到低遍历
1010,第一位是1,此时last=0,res=0,我们可以从第2-4位中任意选(K-last)(2)位填1,即res+= C 3 2 C_{3}^{2} C32,last++,
②第二位是
0,此时res=3,last=1,跳过③第三位是
1,此时res=3,last=1,从第4位任意选(K-last)(1)位填1,即res+= C 1 1 C_{1}^{1} C11,last++,④此时res=4,last=2,K-last=0,所有数字已遍历完,这是最后一种情况,也就是
1010本身,故还需res++。最终结果就是 res=5。
#include<stdio.h>
#include<algorithm>
#include<string.h>
#include<sstream>
#include<time.h>
#include<math.h>
#include<vector>
#include<iostream>
using namespace std;
#define ll long long
#define INF 0x3f3f3f3f3f3f
/*---------------------------------------------------------------*/
const int N = 35;
int f[N][N];//f[i][j]表示从i个数里选j个数
int K,B;
void init(){
for(int i=0;i<N;i++)
for(int j=0;j<=i;j++)
if(!j) f[i][j]=1;
else f[i][j]=f[i-1][j]+f[i-1][j-1];
}
int dp(int n){
if(!n) return 0;
vector<int> nums;
while(n) nums.push_back(n%B),n/=B;
int res=0;//答案的数量
int last=0;//前面已经确定多少1
for(int i=nums.size()-1;i>=0;i--){//最高位往最低位枚举
int x=nums[i];
//x>0求左分支和右分支的情况
if(x){
res+=f[i][K-last];//x大于0,这一位一定可以填0,剩下i位(0~i-1)选K-last位,
if(x>1){//再看x是否大于1,即是否可以填1
if(K-last-1>=0)//判断是否还有1没填完
res+=f[i][K-last-1];//是就在剩下i位(0~i-1)选K-last-1位
break;//统计完成
}
else{//当前位为1,进入到右侧分支进行讨论
last++;
if(last>K)//超过了K退出循环
break;
}
}
//最右侧分支的方案(数本身),也是判断是否是有K个1
if(!i&&last==K) res++;
}
return res;
}
/*---------------------------------------------------------------*/
int main(){
clock_t starttime,endtime;
starttime=clock();
/*---------------------------------------------------------------*/
init();
int l,r;
cin>>l>>r>>K>>B;
cout<<dp(r)-dp(l-1)<<endl;
/*---------------------------------------------------------------*/
endtime=clock();
printf("\n耗时:%f s\n",(double)(endtime-starttime)/CLOCKS_PER_SEC);
return 0;
}
数字游戏

#include<stdio.h>
#include<algorithm>
#include<string.h>
#include<sstream>
#include<time.h>
#include<math.h>
#include<vector>
#include<iostream>
using namespace std;
#define ll long long
#define INF 0x3f3f3f3f3f3f
/*---------------------------------------------------------------*/
const int N=15;
int f[N][N];//f[i][j]表示一共有i位 ,且最高位填j的数的个数
void init(){
for(int i=0;i<=9;i++) f[1][i]=1;
for(int i=2;i<N;i++)
for(int j=0;j<=9;j++)
for(int k=j;k<=9;k++)
f[i][j]+=f[i-1][k];
}
int dp(int n){
if(!n) return 1;
vector<int> nums;
while(n) nums.push_back(n%10),n/=10;
int res=0;
int last=0;
for(int i=nums.size()-1;i>=0;i--){
int x=nums[i];
for(int j=last;j<x;j++)
res+=f[i+1][j];//共i+1位,最高位填j
//判断该位能不能填x
if(x<last) break;
last=x;
if(!i) res++;
}
return res;
}
/*---------------------------------------------------------------*/
int main(){
clock_t starttime,endtime;
starttime=clock();
/*---------------------------------------------------------------*/
int l,r;
init();
while(cin>>l>>r) cout<<dp(r)-dp(l-1)<<endl;
/*---------------------------------------------------------------*/
endtime=clock();
printf("\n耗时:%f s\n",(double)(endtime-starttime)/CLOCKS_PER_SEC);
return 0;
}
Windy数
#include<stdio.h>
#include<algorithm>
#include<string.h>
#include<sstream>
#include<time.h>
#include<math.h>
#include<vector>
#include<iostream>
using namespace std;
#define ll long long
#define INF 0x3f3f3f3f3f3f
/*---------------------------------------------------------------*/
const int N=11;
int f[N][10];
void init(){
for(int i=0;i<=9;i++) f[1][i]=1;
for(int i=2;i<N;i++){
for(int j=0;j<=9;j++)
for(int k=0;k<=9;k++)
if(abs(j-k)>=2)
f[i][j]+=f[i-1][k];
}
}
int dp(int n){
if(!n) return 0;
vector<int> nums;
while(n) nums.push_back(n%10),n/=10;
int res=0;
int last=-2;
for(int i=nums.size()-1;i>=0;i--){
int x=nums[i];
for(int j=(i==nums.size()-1);j<x;j++){
if(abs(j-last)>=2)
res+=f[i+1][j];
}
if(abs(x-last)>=2) last=x;
else break;
if(!i) res++;
}
//特殊处理有前导0的数
for(int i=1;i<nums.size();i++)
for(int j=1;j<=9;j++)
res+=f[i][j];
return res;
}
/*---------------------------------------------------------------*/
int main(){
clock_t starttime,endtime;
starttime=clock();
/*---------------------------------------------------------------*/
init();
int l,r;
scanf("%d%d",&l,&r);
printf("%d",dp(r)-dp(l-1));
/*---------------------------------------------------------------*/
endtime=clock();
printf("\n耗时:%f s\n",(double)(endtime-starttime)/CLOCKS_PER_SEC);
return 0;
}
STL
std::vector
定义于头文件
是封装动态数组的容器。
元素相继存储,这意味着不仅可通过迭代器,还能用指向元素的常规指针访问元素。
vector 的存储是自动管理的,按需扩张收缩。 vector 通常占用多于静态数组的空间,因为要分配更多内存以管理将来的增长。
vector 所用的方式不在每次插入元素时,而只在额外内存耗尽时重分配。分配的内存总量可用 capacity() 函数查询。额外内存可
通过对 shrink_to_fit() 的调用返回给系统。
元素访问:operator[]或迭代器。
成员函数
| begin() | 返回起始的迭代器 |
|---|---|
| end() | 返回指向末尾的迭代器 |
| rbebin() | 返回指向起始的逆向迭代器 |
| rend() | 返回指向末尾的逆向迭代器 |
| empty() | 检查容器是否为空 |
| size() | 返回容纳的元素数 |
| clear() | 清除内容 |
| erase(iterator pos) erase(iterator first,iterator second) 时间复杂度均为O(N) | 擦除位于pos元素 移除范围[first,last)中的元素 |
| push_back() | 将元素添加到末尾 |
| pop_back() | 移除末尾元素 |
| insert(it,x) 时间复杂度O(N) | 在迭代器it处插入一个元素x |
std::basic_string
定义于头文件
为操作任何字符类型的字符串设计的模板类。
通过下标或迭代器访问。
如果要读入和输出整个string字符串,则只能用cin和cout。
成员函数
1、find
寻找首个等于给定字符序列的子串。搜索始于 pos ,即找到的子串必须不始于 pos 之前的位置。
size_type find( const basic_string& str, size_type pos = 0 ) const;
查询首个等于str的字串
size_type find( CharT ch, size_type pos = 0 ) const;
查询首个等于ch的字符
没有查到返回npos(常数-1,unsigned_int类型的最大值)。
2、find_first_of
寻找字符的首次出现
3、find_last_of
寻找字符的最后一次出现
4、insert
插入字符
5、erase
移除字符
str.erase(it)用于删除单个字符。
str.erase(first,last)删除[first,last)的元素。
6、replace
替换字符串的指定位置
str.replace(pos,len,str2)把str从pos位开始、长度为len的子串替换为str2。
str.replace(it1,it2,str2)把str的迭代器[it1,it2)范围的子串替换为str2。
7、operator+=
将两个string直接拼起来。
8、比较运算符
<=、>=、>、<、==、!=比较的都是字典序。
9、substr()
str.substr(pos,len)返回从pos号位开始、长度为len的子串,时间复杂度为O(len)。
map
std::map 是有序键值对容器,它的元素的键是唯一的。用比较函数 Compare 排序键。搜索、移除和插入操作拥有对数复杂度。 map 通常实现为红黑树。
| 成员函数 | 作用 |
|---|---|
| size() 时间复杂度O(1) | 返回容纳的元映射对数 |
| empty | 检查容器是否为空 |
| clear() 时间复杂度O(N) | 清除内容 |
| insert | 插入元素或结点 |
| erase(it) 时间复杂度O(1) size_type erase( const key_type& key ); 时间复杂度O(logN) mp.erase(first,last) 时间复杂度O(last-first) | 擦除元素 移除关键等于 key 的元素(若存在一个)。删除区间[first,last)的元素 |
| count | 返回匹配特定键的元素数量 |
| find(key) 时间复杂度O(logN) | 寻找带有特定键的元素,返回该键的映射的迭代器 |
| contains | 检查容器是否含有带特定键的元素 |
| lower_bound | 返回指向首个不小于给定键的元素的迭代器 |
| upper_bound | 返回指向首个大于给定键的元素的迭代器 |
set
set是一个内部自动有序且不含重复元素的容器。
set只能通过迭代器访问。
除开vector和string之外的容器都不支持*(it+i)的访问方式。
常用函数
(1)insert()
st.insert(x)将x插入set容器中,并自动递增排序和去重,时间复杂度O(logN)。
(2)find()
find(value)返回set中值为value的迭代器,时间复杂度为O(logN)。
(3)erase()
st.erase(it),it为所需要删除元素的迭代器,时间复杂度为O(1)。可以结合find()函数来使用。
st.erase(vlaue),value为需要删除元素的值,时间复杂度为O(logN)。
st.erase(first,last),删除[first,last)的元素
(4)size()
获得set内元素的个数,时间复杂度O(1)。
(5)clear()
st.clear()清空set内所有元素,时间复杂度为O(N)。
queue
std::queue 类是容器适配器,它给予程序员队列的功能——尤其是 FIFO (先进先出)数据结构。queue 在底层容器尾端推入元素,从首端弹出元素。
只能通过front()来访问队首元素,通过back()来访问队尾元素。
push()
fornt()
back()
pop()
empty()
size()
练习题
123

关键是求得任意位置所在组号和在组内位置,
(
n
−
1
)
∗
n
2
<
x
≤
n
∗
(
n
+
1
)
2
n
=
r
o
u
n
d
(
2
∗
x
)
\frac{(n-1)*n}{2}<x\leq\frac{n*(n+1)}{2}\\ n=round(\sqrt[] {2*x})
2(n−1)∗n<x≤2n∗(n+1)n=round(2∗x)
pair<ll,ll> getN(ll x){
ll n=round(sqrt(2*x));//四舍五入
return {n,x-(n-1)*n/2};//返回组号和组内位置或称之为值
}
异或变换

先模拟,找出循环节(循环多次后变为同样的二进制串)。
假设总共变换n次,而在变换t次后变为初始串,再经过t次也是同样结果,我们要避免剩下多余的运算,故再继续变换(n-t)/t次就够了。
PAT甲级 1018 测试点8,9
#include<iostream>
#include<queue>
#include<vector>
#include<cstring>
#include<limits.h>
using namespace std;
const int INF=99999999;
const int MAXN=510;
typedef long long ll;
int CMax,N,SP,M;
struct Node {
int u;
int dis;
int capacity;
bool operator>(const Node&a)const {
return dis>a.dis;
}
} node[MAXN];
struct Edge {
int v,w;
Edge(int v,int w):v(v),w(w){
}
};
vector<Edge> Adj[MAXN];
bool vis[MAXN];
vector<int> pre[MAXN];
int min_dis[MAXN];
priority_queue<Node,vector<Node>,greater<Node> > q;
int k=0;
void dijkstra() {
fill(min_dis,min_dis+MAXN,INF);
q.push(node[0]);
min_dis[0]=0;
while(!q.empty()) {
int u=q.top().u;
q.pop();
if(vis[u]) continue;
vis[u]=true;
for(vector<Edge>::iterator i=Adj[u].begin();i!=Adj[u].end();i++) {
int v=i->v,w=i->w;
if(vis[v]) continue;
if(min_dis[v]>min_dis[u]+w) {
min_dis[v]=min_dis[u]+w;
node[v].dis=min_dis[v];
q.push(node[v]);
pre[v].clear();
pre[v].push_back(u);
}
else if(min_dis[v]==min_dis[u]+w) pre[v].push_back(u);
}
}
}
int minSent=INF,minBack=INF;
vector<int> temppath,path;
void dfs(int v){
temppath.push_back(v);
if(v==0){
int sent=0,back=0;
for(int i=temppath.size()-1;i>=0;i--){
int id=temppath[i];
int t=node[id].capacity-(CMax>>1);
if(t>0){
back+=t;
}
else{
if(back>(0-t)) back+=t;
else sent+=((0-t)-back),back=0;
}
}
if(sent<minSent||sent==minSent&&back<minBack){
minSent=sent;
minBack=back;
path=temppath;
}
temppath.pop_back();
return;
}
for(int i=0;i<pre[v].size();i++)
dfs(pre[v][i]);
temppath.pop_back();
}
int main(){
cin>>CMax>>N>>SP>>M;
for(int i=1; i<=N; i++)
cin>>node[i].capacity,node[i].u=i;
for(int i=0; i<M; i++) {
int x,y,w;
cin>>x>>y>>w;
Edge e= {y,w};
Adj[x].push_back(e);
}
dijkstra();
node[0].capacity=CMax>>1;
dfs(SP);
printf("%d 0", minSent);
for(int i = path.size() - 2; i >= 0; i--)
printf("->%d", path[i]);
printf(" %d", minBack);
return 0;
}
/*
10 3 3 5
3 2 2
0 1 1
0 2 1
0 3 3
1 3 1
2 3 1
*/





















 4万+
4万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








