R与统计分析

本文主要来自<<Modern Applied Statistic with S>>一书

1. 基础知识

（1）factor重命名

#################################################################
# 将因素型转换重新命名
#################################################################
factorTest <- factor(c('just so so ','good', 'better', 'better', 'good', 'best', 'good', 'better'))
factorTest
factorLable <- ordered(factorTest, labels = c(">90", '80-90', '70-80', '<70'))
factorLable

（2）基本操作函数

search()
objects()
rm(list = ls())
find("objects")

（3）单变量统计分析

x <- rt(250, df = 9)
par(pty = "s")
qqnorm(x)
qqline(x)


# 拟合数据属于何种分布，可使用MASS包中的fitdistr()
library(MASS)
x <- rgamma(100, shape = 5, rate = 0.1)
fitdistr(x, 'gamma')

x2 <- rt(250, df = 9)
fitdistr(x2, "t", df = 9)

fitdistr(x2, 't')



data(shoes)
head(shoes)
shoes

（4）数据录入

mydata <- data.frame(id = 1, name = 'Lily', age = 10)
Edit.data(mydata)
fix(mydata)  #更改数据并保存
edit(mydata) #仅修改数据
mydata

2. Linear Statistical Model

（1）方差分析实例

library(MASS)
whiteside
str(whiteside)

?xyplot
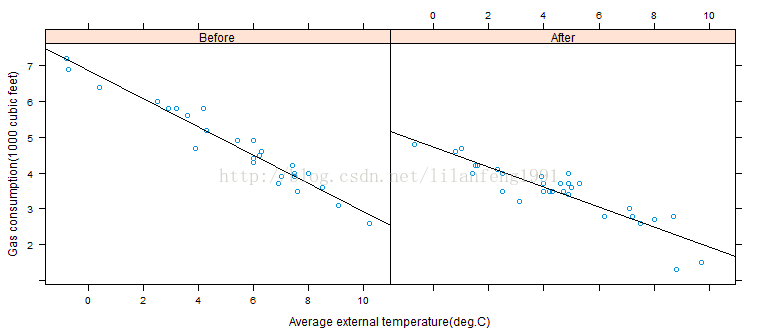
xyplot(Gas ~ Temp | Insul, whiteside, panel = function(x, y, ...) {
  panel.xyplot(x, y, ...)
  panel.lmline(x, y, ...)
}, xlab = "Average external temperature(deg.C)", 
ylab = "Gas consumption(1000 cubic feet)",
aspect = "xy",
strip = function(...) strip.default(..., style = 1)
)

?lm
##############################
#构建Insul等于"Before"的模型
##############################
gasB <- lm(Gas ~ Temp, data = whiteside, subset = Insul == 'Before')
##############################
#update用于更改模型
##############################
gasA <- update(gasB, subset = Insul == 'After')

############################################################
#fitted model objects
#对模型的更进一步操作包括：
# print： 简单的display
# summary： 分析output
# coef（coefficient）：提取出regression coefficeints
# resid（residuals）：残差
# fitted（fitted.values）：拟合值
# deviance: redisual sum of squares
# anova：方差分析
# predict：对新数据的means或standard errors的预测
# plot： 诊断图
############################################################


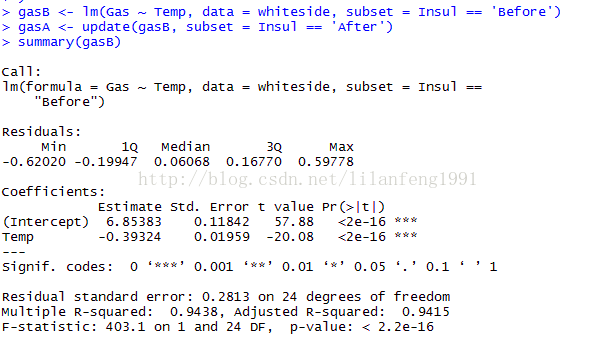
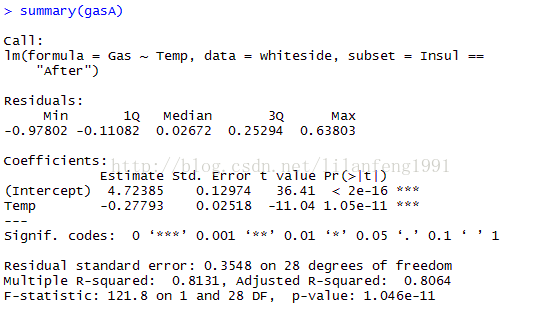
summary(gasB)


summary(gasA)

########################################
# 样本方差分析
########################################
gasB
summary(gasB)
deviance(gasB)
gasB$df.resid
varB <- deviance(gasB)/gasB$df.resid  #直接计算
varB

varB1 <- summary(gasB)$sigma^2  #可供选择的方案，等同于直接计算
varB1

#####################################################################################################
#将两个模型整体到一个里面去
# a/x术语的意义是：a是一个factor，在不同a的水平上x对应的模型
# 本例中 Insul/Temp - 1意思是在不同Insul水平上，对应的Temp模型，- 1表示省略掉截距
#####################################################################################################
gasBA <- lm(Gas ~ Insul/Temp - 1, data = whiteside)
summary(gasBA)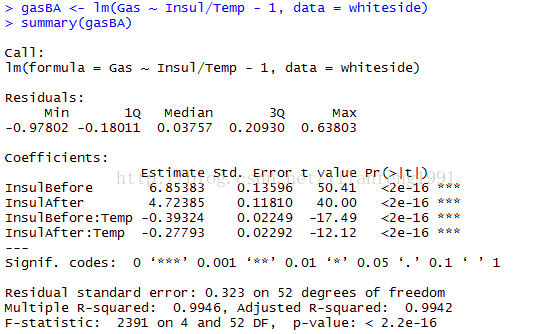

##############################
# 拟合曲线
# 'identity' function I(...)
##############################
gasQ <- lm(Gas ~ Insul/(Temp + I(Temp^2)) - 1, data = whiteside)
summary(gasQ)
summary(gasQ)$coef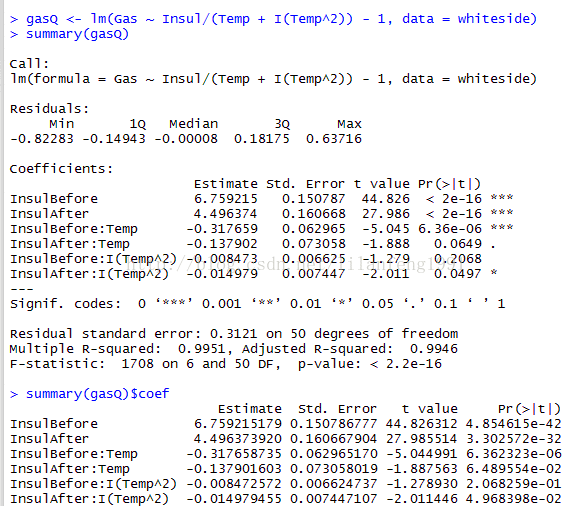

##########################################################
# parallel regression
# R: options(contrasts = c("contr.helmert", "contr.poly"))
##########################################################
gasPR <- lm(Gas ~ Insul + Temp, data = whiteside)
gasPR
anova(gasPR, gasBA) #方差分析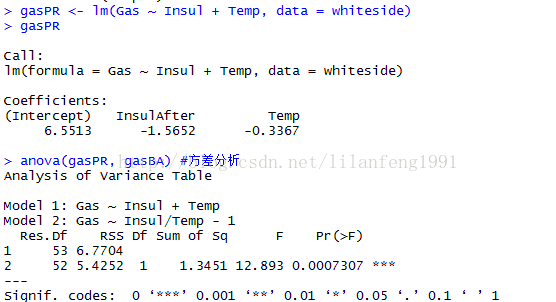

#####################################
# 使用不同的参数，分开slopes来拟合模型
#####################################
options(contrasts = c("contr.treatment", "contr.poly"))
gasBA1 <- lm(Gas ~ Insul*Temp, data = whiteside)
summary(gasBA1)$coef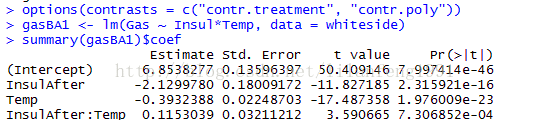

（2）回归诊断实例

模型拟合可通过残差的分析来判断

library(MASS)
head(hills)
str(hills)
(hills.lm <- lm(time ~ dist + climb, data = hills))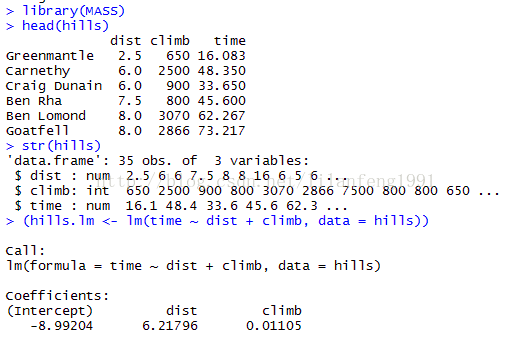

frame()  # create/start a new plot frame
par(fig = c(0, 0.6, 0, 1))
??fig
plot(fitted(hills.lm), studres(hills.lm))
abline(h = 0, lty = 2)
identify(fitted(hills.lm), studres(hills.lm), row.names(hills))
par(fig = c(0.6, 1, 0, 1), pty = "s", new = TRUE)
qqnorm(studres(hills.lm))
qqline(studres(hills.lm))
hills.hat <- lm.influence(hills.lm)$hat
cbind(hills, lev = hills.hat)[hills.hat > 3/35, ]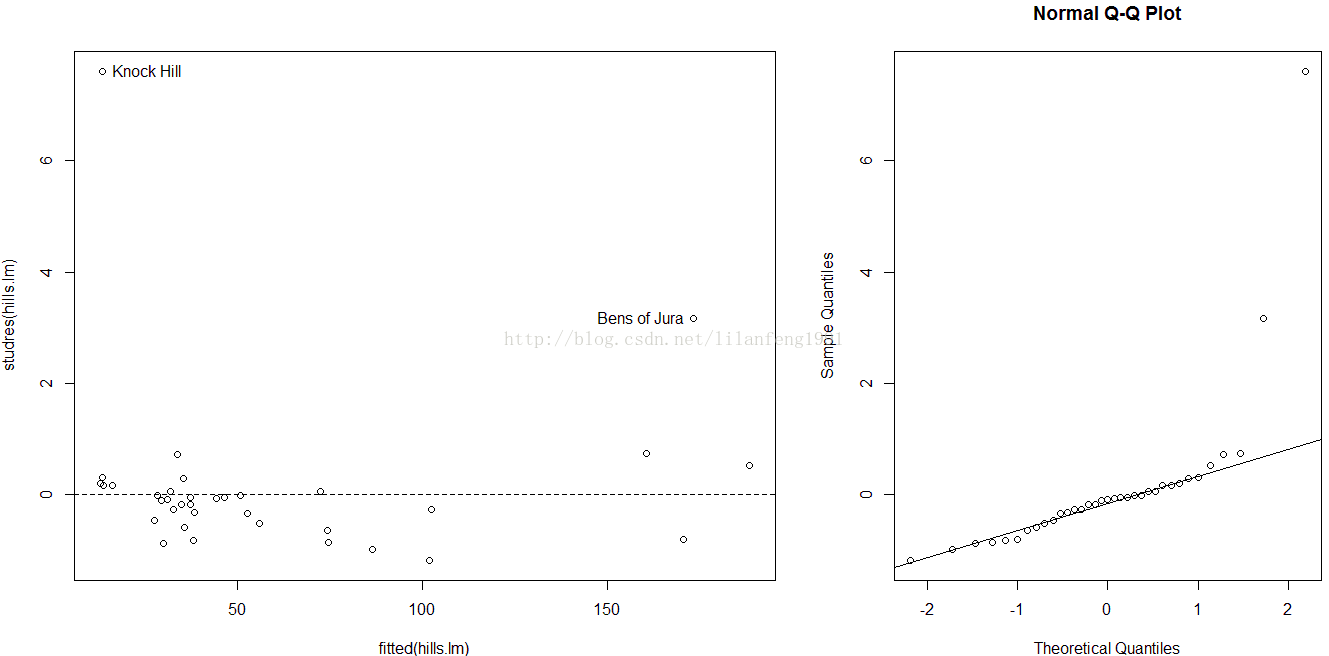

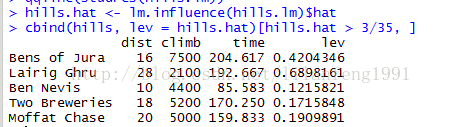
#查看Knock Hill的预测值
cbind(hills, pred = predict(hills.lm))["Knock Hill", ]

(hills1.lm <- update(hills.lm, subset = -18))

#######################################################
# 可以看到踢除Knock Hill对模型参数没有较大影响
# 考虑检测一下其他两个离异点
#######################################################
update(hills.lm, subset = - c(7, 18))
summary(hills1.lm)

summary(update(hills1.lm, weights = 1/dist^2))

lm(time ~ -1 + dist + climb, hills[-18, ], weights = 1/dist^2)

hillsNew <- hills
head(hillsNew)
hillsNew$ispeed <- hillsNew$time/hillsNew$dist
hillsNew$grad <- hillsNew$climb/hillsNew$dist
(hills2.lm <- lm(ispeed ~ grad, data = hillsNew[-18, ]))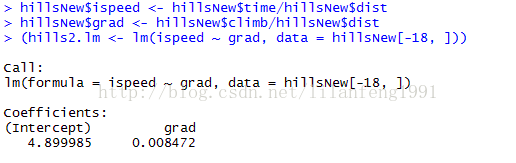

frame()
par(fig = c(0, 0.6, 0, 1))
plot(hillsNew$grad[-18], studres(hills2.lm), xlab = 'grad')
abline(h = 0, lty = 2)
identify(hillsNew$grad[-18], studres(hills2.lm), row.names(hillsNew)[-18])
par(fig = c(0.6, 1, 0, 1), pty = 's', new = TRUE)
qqnorm(studres(hills2.lm))
qqline(studres(hills2.lm))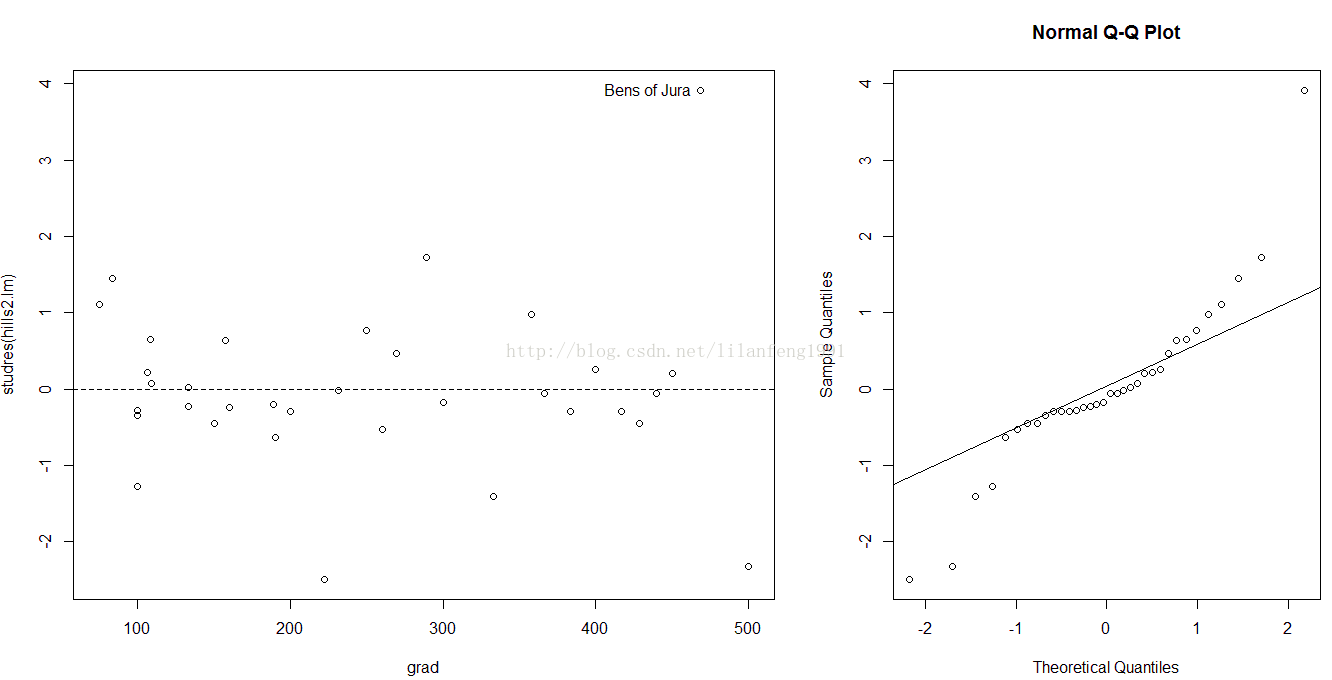

hills2.hat <- lm.influence(hills2.lm)$hat
cbind(hillsNew[-18, ], lev = hills2.hat)[hills2.hat > 1.8*2/34, ]