主要讲解字符串处理的一般小算法集合。
- 最长公共子序列 LCS
- 最长递增子序列 LIS
- 最长回文子串
- 字符串包含问题
- hash思想解决字符串问题
- 实现子串查找函数strstr
- 实现字符串转成整型函数atoi
- 实现字符串拷贝函数strcpy
- 实现字符串中单词倒置
- 字符串的子串问题
1.1最长公共子序列 LCS
问题描述:Longest Common Subsequence,一个序列 S ,如果分别是两个已知序列X和Y的子序列(不一定连续,但是顺序不能乱),且是所有子序列中最长的,则 S 称为这两个已知序列的最长公共子序列。例如,字符串13455与245576的最长公共子序列为455,字符串acdfg与akdfc的最长公共子序列为adf。
问题分析:LCS可以描述两段文字之间的“相似度”,判断抄袭程度。注意与Longest Common Substring最长公共子串的区别。
问题解决:
枚举法:假定字符串X/Y的长度分别为m/n,则X共有2m个不同子序列,对X的每一个子序列,检查它是否也是Y的子序列,在检查过程中选出最长的公共子序列;时间复杂度是指数级O(2m .2n)。
动态规划:二维数组c[i,j]记录序列Xi和Yj的最长公共子序列的长度。其中Xi=< x1, x2, …, xi >,Yj=< y1, y2, …, yj >
Procedure LCS_LENGTH(X,Y);
begin
m:=length[X];
n:=length[Y];
for i:=1 to m do c[i,0]:=0;
for j:=1 to n do c[0,j]:=0;
for i:=1 to m do
for j:=1 to n do
if x[i]=y[j] then
begin
c[i,j]:=c[i-1,j-1]+1;
b[i,j]:="↖";
end
else if c[i-1,j]≥c[i,j-1] then
begin
c[i,j]:=c[i-1,j];
b[i,j]:="↑";
end
else
begin
c[i,j]:=c[i,j-1];
b[i,j]:="←"
end;
return(c,b);
end;
数组b[i,j]标记c[i,j]的值是由哪一个子问题的解达到的。即c[i,j]是由c[i-1,j-1]+1或者c[i-1,j]或者c[i,j-1]的哪一个得到的。取值范围为Left,Top,LeftTop三种情况。LCS_LENGTH和LCS时间复杂度分别是Ο(mn)和Ο(m+n)。
Procedure LCS(b,X,i,j);
begin
if i=0 or j=0 then return;
if b[i,j]="↖" then
begin
LCS(b,X,i-1,j-1);
print(x[i]); //打印x[i]
end
else if b[i,j]="↑" then LCS(b,X,i-1,j)
else LCS(b,X,i,j-1);
end;
如果列出所有的最长公共子序列,B的取值范围从1,2,3扩展到1,2,3,4。LCS_LENGTH 算法中if c[i-1,j]=c[i,j-1],b[i,j]=4。LCS算法中采用广度优先遍历即可。
Procedure LCS(b,X,i,j,reLen=LCS_LENGTH);
begin
if i=0 or j=0 then printall(result[]); //for循环一次性输出一个可行的结果
if b[i,j]="↖" then
begin
result[reLen --]=x[i-1];
LCS(b,X,i-1,j-1,reLen);
end
else if b[i,j]="↑" then LCS(b,X,i-1,j,reLen)
else if b[i,j]=" ←" then LCS(b,X,i,j-1,reLen)
else
begin
LCS(b,X,i,j-1,reLen);
LCS(b,X,i-1,j,reLen);
end
end;
1.2最长递增子序列 LIS
问题描述:Longest Increasing Subsequence,给定一个长度为N的数组,找出一个最长的单调递增子序列(不一定连续,但是顺序不能乱)。例如:给定一个长度为6的数组A{5, 6, 7, 1, 2, 8},则其最长的单调递增子序列为{5,6,7,8},长度为4。
问题分析:其实此LIS问题可以转换成LCS问题,假设A′={1,2,5,6,7,8}, 则A与A′的LCS即是A的LIS。
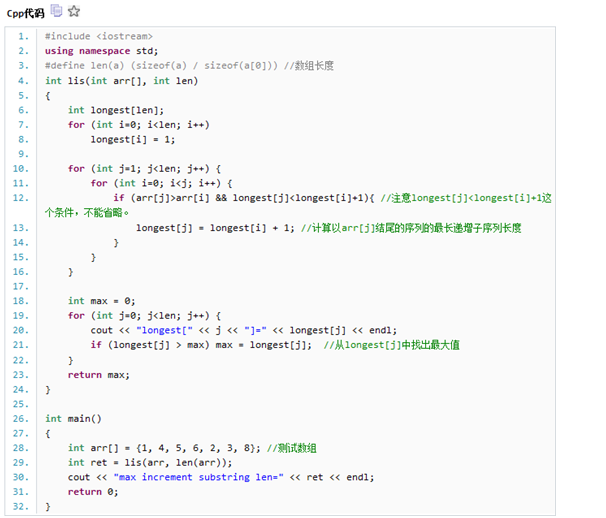
问题解决:本题也可以用动态规划解决。设长度为N的数组为{a0,a1, a2, …an-1},则假定以aj结尾的数组序列的最长递增子序列长度为L(j),则L(j)={ max(L(i))+1, i小于j且a[i]小于a[j] }。也就是说,我们需要遍历在j之前的所有位置i(从0到j-1),找出满足条件a[i]小于a[j]的L(i),求出max(L(i))+1即为L(j)的值。最后,我们遍历所有的L(j)(从0到N-1),找出最大值即为最大递增子序列。时间复杂度为O(N2)。
1.3最长回文子串
问题描述:给定字符串str,求str最长的回文子串。
问题分析:注意aba,abba,都是回文字符串。字符个数有奇偶之分。
问题解决:
枚举法:考虑奇偶情况,枚举回文字符串的中心。时间复杂度O(N2)。
int LongestPalindrome(const char *s, int n)
{ int i, j, max;
if (s == 0 || n < 1) return 0;
max = 0;
for (i = 0; i < n; ++i) // i is the middle point of the palindrome
{
for (j = 0; (i - j >= 0) && (i + j < n); ++j) // if the length is odd
{
if (s[i - j] != s[i + j]) break;
if (j * 2 + 1 > max) max = j * 2 + 1;
}
for (j = 0; (i - j >= 0) && (i + j + 1 < n); ++j)
// for the even case
{ if (s[i - j] != s[i + j + 1]) break;
if (j * 2 + 2 > max) max = j * 2 + 2;
}
}
return max;
}
Manacher算法: 时间复杂度O(N)。
长度为n的字符串,共有n-1个“邻接”,加上首字符的前面,和末字符的后面,更n+1的“空”(gap)。一般可以用‘#’分隔。因此,字符串本身和gap一起,共有2n+1个,必定是奇数;
字符串12212321→ S[] = ” 美元号 #1#2#2#1#2#3#2#1#”;
用一个数组 P[i] 来记录以字符S[i]为中心的最长回文子串向左/右扩张的长度(包括S[i]),比如S和P的对应关系:
S 美元号 # 1 # 2 # 2 # 1 # 2 # 3 # 2 # 1 #
P 0 1 2 1 2 5 2 1 4 1 2 1 6 1 2 1 2 1
P[i]-1正好是原字符串中回文串的总长度。遍历P数组便可以得到最长回文子串长度。(注:为了防止字符比较时越界,在字符串之前还加了一个特殊字符‘$’,故新串下标是从1开始的)。
void pk()
{
int i;
int mx = 0;
int id;
for(i=1; i<n; i++)
{
if( mx > i )
p[i] = MIN( p[2*id-i], mx-i );
else
p[i] = 1;
for(; str[i+p[i]] == str[i-p[i]]; p[i]++);
if( p[i] + i > mx )
{
mx = p[i] + i;
id = i;
}
}
}
由于这个算法是线性从前往后扫的。那么当我们准备求P[i]的时候,i以前的P[j]我们是已经得到了的。我们用mx记在i之前的回文串中,延伸至最右端的位置。同时用id这个变量记下取得这个最右边位置mx时的i值。
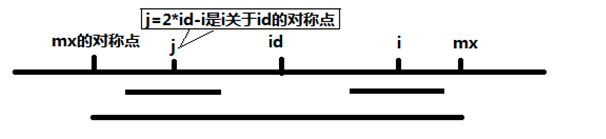
当 mx - i > P[j] 的时候,以S[j]为中心的回文子串包含在以S[id]为中心的回文子串中,由于 i 和 j 对称,以S[i]为中心的回文子串必然包含在以S[id]为中心的回文子串中,所以必有 P[i] = P[j]:
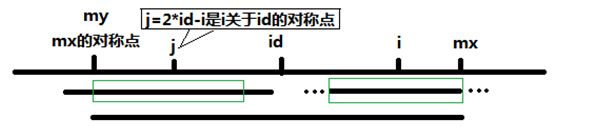
当 mx - i <= P[j] 的时候,以S[j]为中心的回文子串不一定完全包含于以S[id]为中心的回文子串中,但是基于对称性可知,下图中两个绿框所包围的部分是相同的,也就是说以S[i]为中心的回文子串,其向右至少会扩张到mx的位置,也就是说 P[i] >= mx-i,实际上,由于S[id-mx] != S[id+mx],S[2*i-mx-1]=S[j+mx-i]=S[id-mx]!=S[id+mx],所以P[i]=mx+i;for循环第一次变会fail。
1.4字符串包含问题
问题描述:LongString是否包含ShortString,即Short每个字符是否在LongString中
问题分析:方法有很多,关键看时间复杂度。
问题解决:
int CompareString1(string LongString,string ShortString)
{//O(n*m);
for(int i=0;i<ShortString.length();i++)
{ int j=0;
for( j=0;j<LongString.length();j++)
if(ShortString[i]==LongString[j]) break;
if(j==LongString.length()) return 0;
}
return 1;
}
int CompareString2(string LongString,string ShortString)
{//先排序在比较时间复杂度:O(mlogm)+O(nlogn)+O(m+n)
sort(& LongString[0],& LongString[0]+LongString.length());//algorithm.h
sort(& ShortString[0],& ShortString[0]+ShortString.length());
int l=0,s=0;
while( s<ShortString.length())
{ if(LongString[l]==ShortString[s]){s++;continue;}
while(LongString[l]<ShortString[s] && l<LongString.length()-1) l++;//L[l]小,下标l不能过界
if(LongString[l]!=ShortString[s]) return 0;//L[l]大
}
return 1;
}
int CompareString3(string LongString,string ShortString)
{//O(m+n) Hash表
int a[256]={0};//初始化时元素个数比数组少,剩下的元素都回被初始化为0
for(int i=0;i<LongString.length();i++) a[LongString[i]]++;
for(int j=0;j<ShortString.length();j++)
if(a[ShortString[j]]==0) return 0;
/*else a[ShortString[j]]--;*/
return 1;
}
//字符串严格包含:两个字符串中所含有的字符和个数都相同
bool IsMatch(const char * str1,const char * str2)
{ int hash[256]={0};
for(int i=0;i<strlen(str1);i++) hash[str1[i]]++;
for(int j=0;j<strlen(str2);j++)
{ if(hash[str2[j]]==0) return false;
else hash[str2[j]]--; }
return true;
}
1.5 hash思想解决字符串问题
问题描述:略。
问题分析:关键是建立hash字符串数组hash[256],
问题解决:
//在一个字符串中找到第一个只出现一次的字符。
char Find_first_unique_char(char * str)
{ if(!str) return '\0';
int hash[256]={0};
for(int i=0;i<strlen(str);i++)
hash[str[i]]++;
for(int j=0;j<strlen(str);j++)
if(hash[str[j]]==1)
return str[j];
return '\0';
}
1.6实现子串查找函数strstr
问题描述:查找字符串substr在另一个字符串str中首次出现的位置。
问题分析:字符串子串问题:相当于实现strstr库函数
问题解决:
char * MyStrstr(const char * str,const char * substr)
{//O(mn);返回子串substr在str中的位置地址
if(!str || !substr) return NULL;
int s1=strlen(str); int s2=strlen(substr);
if(s1==0 || s2==0) return NULL;
for(int i=0;i<=s1-s2;i++)//len1-len2+1次循环
{ int j=0;
for( j=0;j<s2;j++)
if(str[i+j]!=substr[j]) break;
if(j==s2) return (char *) &str[i];
}
return NULL;//len1<len2
}
1.7实现字符串转成整型函数atoi
问题描述:字符串转换成整数
问题分析:问题本身不难,但是要注意考虑正负号问题;考虑空字符串和空指针问题;考虑非法字符问题;考虑整数越界问题。
问题解决:
long int str_int(string str)//atoi函数
{ assert(str.size()>0); //if(str.size()==0) exit(0);//exit直接把进程给终止啦
int i=0, flag=1;
if(str[i]=='+') i++;
else if(str[i]=='-') {flag=-1;i++;}
long int num=0;
while(i<str.length())
{//string 中size和length函数相同,length是沿用C语言规则,size便于符合STL的接口规则
assert(str[i]>='0'); assert(str[i]<='9'); //if(str[i]<'0' || str[i]>'9') exit(0);
num=num*10+(str[i]-'0');
assert(num>=0);//if(num<0) exit(0);//数据溢出~~~
i++;
}
num*=flag;
return num;
}
1.8实现字符串拷贝函数strcpy
问题描述:字符串拷贝
问题分析:问题本身不难,但是要注意考虑字符串覆盖问题;代码简洁问题;
问题解决:
char * MyStrcpy(char * dest,const char *str)
{//没有考虑dest和str有覆盖问题。//返回目的字符串地址为了可以实现链式操作
assert(dest!=NULL && str!=NULL);
char *address=dest;
while((*dest++= * str++)!='\0');
return address;
}
1.9实现字符串中单词倒置
问题描述:将一句话中的单词倒置,标点符号不倒换
问题分析:
问题解决:
//将一句话中的单词倒置,标点符号不倒换
void ReverseSequence(char * str)
{ assert(str!=NULL);
int len=strlen(str);
assert(len>=0);
int i=0,j=len-1;
char temp;
while(i<j){temp=str[i];str[i]=str[j];str[j]=temp;i++;j--;}
i=0; int begin=0,end=0;
while(str[i]!='\0')
{ if(str[i]!=' '){
begin=i;
while(str[i]!=' '&&str[i]!='\0') {i++;}
i--; end=i;
}
while(begin<end)
{temp=str[begin];str[begin]=str[end];str[end]=temp;begin++;end--;}
i++;
}
}
1.10字符串的子串问题
//求一个字符串中连续出现次数最多的子串
pair<int,string> ContinuousSubstr(const string str)
{ vector<string> substr;
int max=1; string maxstr; int len=str.length();
for(int i=0;i<len;i++) substr.push_back(str.substr(i,len-i));//穷举出所有的后缀子串
for(int i=0;i<len;i++)//子串从str[i]开始
{ for(int j=i+1;j<len;j++)//子串到str[j]结束,子串长度为j-i
{ int temp=1;
for(int k=j;k<len;k+=(j-i))//判断子串[i—j]连续出现次数
{ if(substr[i].substr(0,j-i)==substr[k].substr(0,j-i)) temp++;
else break;
}
if(temp>max){max=temp; maxstr=substr[i].substr(0,j-i);}
}
}
return make_pair(max,maxstr);
}
int ContinuousSubChar(char * str,char * sub)//C语言实现, 注意strncmp/memcpy函数 //的使用,需要在函数外面事先分配子串sub的内存
{ assert(str!=NULL);
int i,j,k; int len=strlen(str);
assert(len>=0);
int max=0;
for(i=0;i<len;i++)
{ for(j=i+1;j<len;j++)
{ int temp=1;
for(k=j;k<len;k+=(j-i))
{ if(strncmp(&str[i],&str[k],j-i)==0) temp++;
else break;
}
if(temp>max){max=temp; memcpy(sub,&str[i],j-i); sub[j-i]='\0';}
}
}
return max;
}
//字符串中出现的相同且长度最长的子串;不止一次出现
string LongestSub(string str)
{//注意find_last_of和rfind不是一回事。
int len=str.size(); int i,j;
string temp;
for(int i=0;i<len;i++)
{ for(j=len-1;j>i;j--)
{ temp=str.substr(i,j);
size_t a,b;
//temp.find_last_of(s)是查找位于s集合中的temp的最后一个字符下标
a=str.find(temp); b=str.rfind(temp);
if(a!=b) return temp;
}
}
return NULL;
}








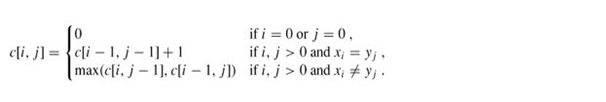














 243
243

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








