关于信息可靠性和有效性的相关调研——准对称离散无记忆信道容量的证明和通过Matlab实现香农编码---韩明伟，刘乐延，王瑄，杨恩发，张祥哲

 目录

一、引言

二、准对称离散无记忆信道容量的证明

三、用Matlab实现香农编码

---

本次调研由韩明伟（P02114217），刘乐延（P02114235），王瑄（P02114020），杨恩发（X02114093），张祥哲（P02114237）共同完成。

一、引言

       信息论是关于通信的理论，是用概率统计的方法研究信息的传输、存储与处理以及如何实现其有效性和可靠性的一门学科。它包括两个基本的问题，一个是信源编码，解决信源的相关性问题，去掉冗余，从而压缩了信源输出，提高了有效性；另一个是信道编码，克服信道中的干扰和噪声，提高了可靠性。其中，信道是通信系统的重要组成部分，它的任务是实现信息的传输可见信道是通信系统的重要组成部分，它的任务是实现信息的传输，在信道固定的情况下，总是希望传输的信息越多越好；另外，信源编码是我们通信系统需要解决的基本问题之一。本文主要研究一种特殊的信道和一种非常经典的编码，即准对称离散无记忆DMC信道和香农编码。

二、准对称离散无记忆信道容量的证明

1、定义：

（1）如果转移概率矩阵P是输入对称而输出不对称，即转移概率矩阵P的每一行都包括同样的元素而各列的元素可以不同，则该对称信道是准对称DMC信道。

（2）由于转移概率矩阵中每行的元素相同，所以H(Y|X)=H(Y|ai)  i=1,2,…,n成立，但每列的元素不相同，所以信道的输入和输出分布概率可能不同，此时H=(Y)的最大值可能小于Y等概时的熵，因此准对称DMC信道的容量：C≤log2m+Σpijlog2pij

2、证明:

定理1：当输入的每一个符号概率都相等时，熵为信道容量C

定理2：设有一个信道，它的输入符号个数有r个，输出符号个数有s个，当且仅当存在常数C使输入分布

p(xi) 满足：①I(xi;Y)=C,p(xi)≠0；②I(xi;Y)<C,p(xi)=0时，I(X;Y) 达极大值。此时，常数C即为所求的信道容量。

定理3：当输入的每一个符号的概率p(xi) 都相等时，准对称信道的容量为：

C=log2r−H(q1,q2,⋯,qs)−∑k=1nNklog2M

其中，r是信道矩阵的行数，q1,q2,⋯,qs 表示信道矩阵P中的任意一行元素，Nk 是第k个子矩阵中行元素之和，Mk 是第k个子矩阵中列元素之和。

证明:

设准对称信道的矩阵为:

P=(p(y1|x1)p(y2|x1)…p(ys|x1)p(y1|x2)p(y2|x2)…p(ys|x2)… p(y1|xr)p(y2|xr)…p(ys|xr))

将矩阵P分为n个对称子阵P1,P2,⋯,Pn;对应的输出符号集Y划分为Y1,Y2,⋯,Yn ;设xi∈X(x1,x2,…,xr) ,则有：

I(xi;Y)=∑Yp(y|xi)log2p(y|xi)p(y)

=∑Yp(y|xi)log2p(y|xi)−∑Yp(y|xi)log2p(y)

因为P是准对称矩阵，它的行元素由{q1,q2,⋯,qs} 排列而成

所以有:

∑Yp(y|xi)log2p(y|xi)=−H(q1,q2,…,qs)   (其中i=1,2,…,r)

设P(xi)=1/r，即输入等概分布，则后一项为：

∑Yp(y|xi)log2p(y)

=∑Yp(y|xi)log2∑Xp(y|xi)p(xi)

=∑Yp(y|xi)log2(1/r)∑Xp(y|xi)

=∑y∈Y1p(y|xi)log2(1/r)∑Xp(y|xi)+∑y∈Y2p(y|xi)log2(1/r)∑Xp(y|xi)

+∑y∈Ynp(y|xi)log2(1/r)∑Xp(y|xi)

因为P1,P2,…,Pn对称，所以有：

∑Xp(y|xi)=M1,y∈Y1

∑Xp(y|xi)=M2,y∈Y2

…

∑Xp(y|xi)=M1,y∈Yn

 都与xi无关，其中Mi为y固定时，矩阵Pi中列元素之和，是一个常数。

∑y∈Y1p(y|xi)=N1

∑y∈Y2p(y|xi)=N2

…

∑y∈Ynp(y|xi)=Nn

其中，Ni表示xi固定时，矩阵Pi中行元素之和，也是一个常数。

所以有：

∑Yp(y|xi)log2p(y)

=N1log2M1/r+N2log2M2/r+⋯+Nnlog2Mn/r

=∑nk=1Nklog2Mk/r

所以得到：

I(xi;Y)=−H(q1,q2,⋯,qs)−∑nk=1Nklog2Mk/r

=log2r−H(q1,q2,⋯,qs)− ∑nk=1Nklog2Mk

=C(常数)

根据定理2，有：

C= log2r−H(q1,q2,⋯,qs)− ∑nk=1Nklog2Mk

证毕

三、用Matlab实现香农编码

1、定义:

（1）变长编码定理：在变长编码中，码长Ki是变化的，可根据信源各个符号的统计特性，如概率大的符号用短码，而对概率小用较长的码，这样在大量信源符号编成码后，平均每个信源符号所需的输出符号数就可以降低，从而提高编码效率。

（2）单符号变长编码定理：若离散无记忆信源的符号熵为H(X)，每个信源符号用m进制码元进行变长编码，一定存在一种无失真编码方法，其码字平均长度Kav满足下列不等式H(X)logm≤Kav<HXlogm+1                         

（3）离散平稳无记忆序列变长编码定理：平均符号熵为HL(X)的离散平稳无记忆信源，必存在一种无失真编码方法，使平均码长Kav满足不等式

HLX≤Kav<HLX+ε

其中ε为任意小正数。

（4）香农编码：从变长编码定理可以看出，要使信源编码后的平均码长最短，就要求信源中每个符号的码长与其概率相匹配，即概率大的信息符号编以短的码字，概率小的符号编以长的码字。由于符号的自信息量 I(xi)就是基于概率计算得到的该符号含有的信息量，因此，将式（1）中的信源熵和平均码长替换成每个信源符号的自信息量I(xi)和码长Ki，则可得到一种构造最佳码长的编码方法，称为香农编码。

2、基于Matlab实现香农编码的过程：

（1）编码思路：香农第一定理指出，选择每个码字的长度Ki满足下式

Ixi≤Ki<Ixi+1,   ∀i

就可以得到这种码。编码思路如下：

①将信源消息符号按其出现的概率大小依次排列为

p1≥p2≥⋯≥pn

②确定满足下列不等式的整数码长Ki为

-log2pi≤Ki≤-log2pi+1

③为了编成唯一可译码，计算第i个消息的累加概率

Pi=k=1i-1pak

④将累加概率Pi变换成二进制数。

⑤取Pi二进制数的小数点后Ki位即为该消息符号的二进制码字。

（2）编码过程：

①规范检查

function  check_p(p)

%检查输入的概率p是否为正确的形式

if ~isempty(find(p<0, 1))

    error('概率不应该小于0！')

end

if abs(sum(p)-1)>10e-10

    error('概率之和不为1，请检查输入！')

end

end

②符号排序

function [p_sequence,name]=p_symbol_sequence(p_1,n)

%p_1是单个符号的概率分布,n是符号序列的符号个数，假设信源是无记忆信源

%此处符号序列排布方式是从低位开始增加

%p_sequence是符号序列的概率密度，name返回的是各个符号的名字

% p_1=sort(p_1,'descend');

% 按照从大到小方式排布

len_p=length(p_1);

p_high=p_1;

name_original={};

for i=1:len_p

    name_original=[name_original,strcat('u',num2str(i))];

end

if n==1

    p_sequence=p_1;

    name=name_original;

end

%对于多重的编码，name是字符串组成的元组，p是数值型，是概率

name_high=name_original;

if n>=2

    for i=2:n

        len_p_high=length(p_high);

        p_tem=[];

        name_tem={};

        for sym_1=1:len_p

            for sym_2=1:len_p_high

                p_tem=[p_tem,p_1(sym_1)*p_high(sym_2)];

                name_tem=[name_tem,strcat(name_original(sym_1),name_high(sym_2))];

            end

        end

        p_high=p_tem;

        name_high=name_tem;

    end

    p_sequence=p_high;

    name=name_high;

end

end

③十进制转二进制

function code_bin=dec2bin_0_1(number_dec)

i=1;

 code_bin=fix(number_dec*2);

 T=number_dec*2-code_bin;

 a(i)=code_bin;

 while (T~=0) && (i<=32)

     i=i+1;

     number_dec=T;

     code_bin=fix(number_dec*2);

     T=number_dec*2-code_bin;

     a(i)=code_bin;

 end

 code_bin=a(1:1:i); 

 %防止输入为0时位数不够报错

 if number_dec==0

     code_bin=zeros(1,33);

 end

 end

④香农编码

function [code_original,len_average,Hx,efficiency_coding] = Shannon_coding(p_1)

%输入要求输入信源概率分布p_1,输出平均码长，信源熵，编码效率

%   此处显示详细说明

%检查p是否符合标准

check_p(p_1)

%变量命名

[~,name]=p_symbol_sequence(p_1,1);

%概率排序

p_1_sort=sort(p_1,'descend');

%计算自信息量

I_x=-log2(p_1_sort);

%计算码长

len_code=ceil(I_x);

%计算累加概率

p_sum=0;

for i=1:length(p_1_sort)-1

    p_sum(i+1)=p_sum(i)+p_1_sort(i);

end

%储存编码的地方

ccode=cell(1,length(p_1_sort));

for i=1:length(p_1_sort)

    code_total=strrep(num2str(dec2bin_0_1(p_sum(i))),' ', '');

    code=code_total(1:len_code(i));

    ccode{i}=code;

end

%排序后的输出

output_rankled=[sprintfc('%g',p_1_sort(1,:));ccode];

%调整输出格式(显示为原始的输入顺序)

p_copy=p_1_sort(1,:);

%p_copy此时是调整后的顺序，即从大到小的顺序

code_original=[];

for i=1:length(p_1)

    index=find(p_copy==p_1(i),1);

    code_original=[code_original,[output_rankled(:,index)]];

    output_rankled(:,index)=[];

    p_copy(:,index)=[];

end

%让输出变得更直观

code_original=[name;code_original];

code_original=[{'变量名';'概率';'编码'},code_original];

disp(code_original)

%计算编码的效率（平均码长，信源熵，编码效率）

p_copy=p_1_sort(1,:);

code_ranked=ccode;

[len_average,Hx,efficiency_coding]=coding_efficiency_indicators(p_copy,code_ranked,2);

% fprintf('平均码长：%f\n',len_average)

% fprintf('信源熵：%f\n',Hx)

% fprintf('编码效率：%f\n',effi)

end

⑤主函数：

clear;clc;

p_1=[0.18,0.2,0.01,0.17,0.15,0.15,0.14];

[code_original,len_average,Hx,efficiency_coding] = Shannon_coding(p_1)

（3）仿真结果：

① 输入：

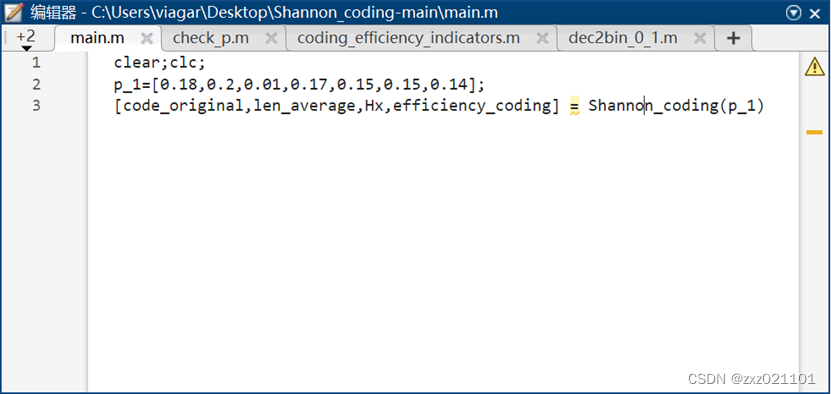
② 输出：