【算法概论】4.图中的路径

4 图中的路径

4.1 距离

两顶点距离 指两者间最短路径的长度

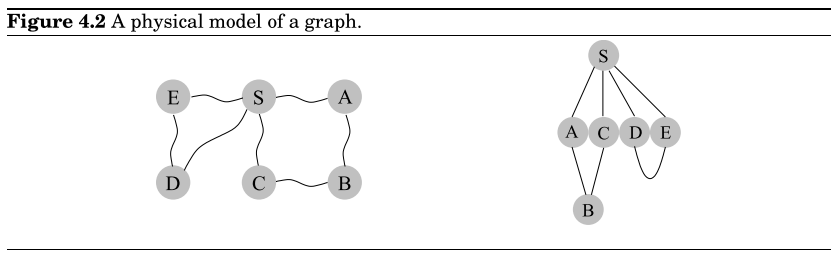
将边 看作绳子，把源点提起，即可得到源点到各点的最短距离

4.2 广度优先搜索

procedure BFS(G,s)
    Input:  Graph G = (V,E),directed or undirected;vertex s ∈ V
    Output: For all vertices u reachable from s,dist(u) is set
            to the distance from s to u.

    for all u ∈ V:
        dist(u)= ∞

    dist(s)=0
    Q=[s] //queue containing just s
    while Q is not empty:
        u=eject(Q)
        for all edges (u,v) ∈ E
            if dist(v)= ∞
                inject(Q,v)
                dist(v)=dist(u)+1

4.3 边的长度

Annotate every edge $e ∈ E$ with a length $l_e$ . If $e = (u, v)$ , we will sometimes also write $l(u, v)\ or\ l_{uv}$.

4.4 Dijkstra算法

4.4.1 广度优先搜索的一个改进

当$边长e = (u, v)$为整数时，在u和v之间增加$l_e-1$个顶点，再运行BFS即可计算G中的距离。

闹钟算法

• 在时刻0为顶点s设定一个闹钟

• 重复以下直到没有闹钟为止：

  假定针对顶点u的下一个闹钟闹铃的时刻为T，则：

  • 从s到u的距离是T。
  • 对于G中u的每个邻居v：
  • 如果还未给v设定闹钟，则为其设定闹钟时刻$T+l(u,v)$
  • 如果v的闹钟时刻设定的比$T+l(u,v)$要晚，则将它设定为$T+l(u,v)$

Dijkstra算法

procedure dijkstra(G,l,s)
    Input:  Graph G=(V,E), directed or undirected;
            positive edge lengths {le:e ∈ E};
            vertex s ∈ V
    Output: For all vertices u reachable from s,dist(u) is set
            to the distance from s to u.

    for all u ∈ V
        dist(u) = ∞
        prev(u) = nil
    dist(s)=0
    H=makequeue(V) //using dist-valus as keys
    while H is not empty:
        u=deletemin(H)
        for all edges (u,v) ∈ E:
            if dist(v) > dist(u)+l(u,v):
                dist(v)=dist(u)+l(u,v)
                prev(v)=u
                decreasekey(H,v)

4.4.2 另一种解释

procedure dijkstra(G,l,s)
    Input:  Graph G=(V,E), directed or undirected;
            positive edge lengths {le:e ∈ E};
            vertex s ∈ V
    Output: For all vertices u reachable from s,dist(u) is set
            to the distance from s to u.

    Initialize dist(s) to 0,other dist(·) to ∞
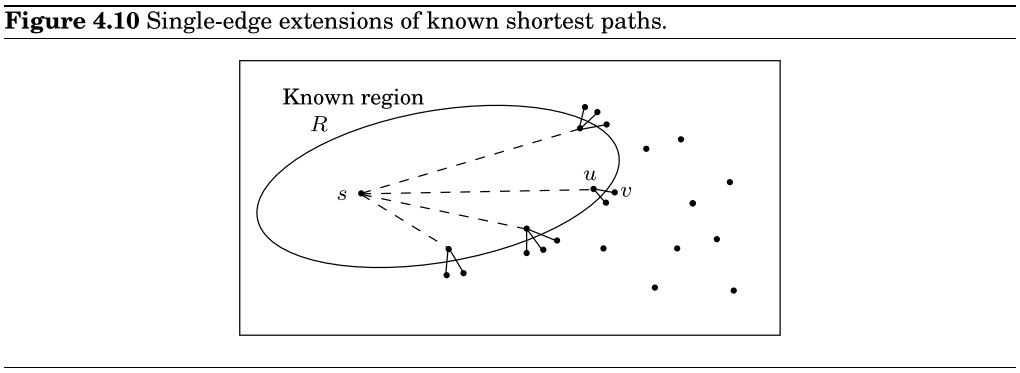
    R={} //the "known regions"
    while R ≠ V:
        Pick the node v ∉ R with smallest dist(·)
        Add v to R
        for all edges (v,z) ∈ E:
            if dist(z) > dist(v)+l(v,z)
                dist(z)=dist(v)+l(v,z)

4.4.3 运行时间

Dijkstra算法结构与BFS相同，一共需要$|V|$次deletemin(H)，和$|V|+|E|$次decreasekey(H,v)；如采用二分堆数据结构实现优先队列，则最优边复杂度为$O(log|V|)$；则算法复杂度为$O((|V|+|E|)log|V|)$。

4.5 优先队列的实现

实现方式	deletemin(H)	decreasekey(H,v)	|V|*del+(|V|+|E|)*decrease
数组	$O(\|V\|)$	$O(1)$	$O(\|V\|^2)$
二分堆	$O(log\|V\|)$	$O(log\|V\|)$	$O((\|V\|+\|E\|)log\|V\|)$
d堆	$O(\frac{d\ log\|V\|}{logd})$	$O(\frac{log\|V\|}{log\ d})$	$O((\|V\|\ d+\|E\|)\frac{log\|V\|}{logd})$
Fibonacci堆	$O(log\|V\|)$	$O(1)$ (平摊后)	$O(\|V\|log\|V\|+\|E\|)$

4.6 含有负边的图的最短路径

4.6.1 负边

Bellman-Ford算法 ：更新所有的边，每条边更新$|V|-1$次。复杂度$O(|V|*|E|)$。

procedure shortest-paths(G,l,s)
    Input:  Graph G=(V,E), directed;
            edge lengths {le:e ∈ E} with no negative cycles;
            vertex s ∈ V
    Output: For all vertices u reachable from s,dist(u) is set
            to the distance from s to u.

    for all u ∈ V
        dist(u)= ∞
        prev(u)= nil
    dist(s)=0
    repeat |V|-1 times:
        for all e ∈ E:
            update(e)

4.6.2 负环

图中一旦出现负环，讨论最短路径没有意义。一旦检测到负环，就要适时地发出警告。

图中存在 负环，当且仅当第|V|次迭代中有某个dist的值被减小。

4.7 有向无环图的最短路径

不存在负环的图：

• 不含 负边 的图
• 不含 环 的图(dag)

procedure dag-shortest-paths(G,l,s)
    Input:  Graph G=(V,E), dag;
            edge lengths {le:e ∈ E};
            vertex s ∈ V
    Output: For all vertices u reachable from s,dist(u) is set
            to the distance from s to u.

    for all u ∈ V
        dist(u)= ∞
        prev(u)= nil
    dist(s)=0
    Linearize G //通过深度优先搜索线性化(拓扑排序)
    for each u ∈ V in Linearized order:
        for all edges (u,v) ∈ E:
            update(u,v)