6 动态规划
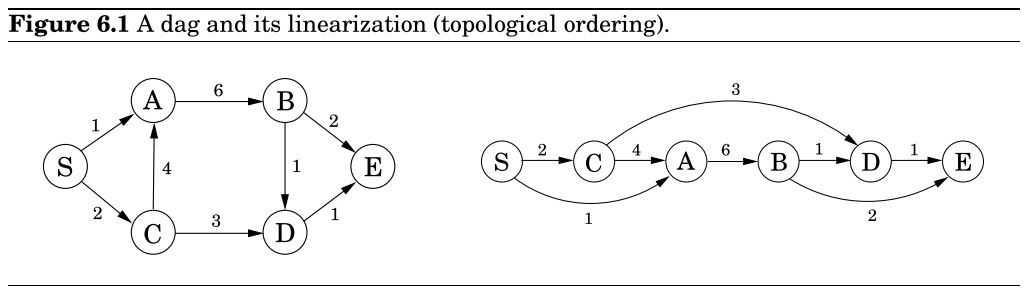
6.1 重新审视DAG的最短路径问题
- 有向无环图DAG的节点可以被线性化:
procedure dag-shortest-paths(G,l,s)
Input: Graph G=(V,E), dag;
edge lengths {le:e ∈ E};
vertex s ∈ V
Output: For all vertices u reachable from s,dist(u) is set
to the distance from s to u.
for all u ∈ V
dist(u)= ∞
dist(s)=0
Linearize G //通过深度优先搜索线性化(拓扑排序)
for each u ∈ V in Linearized order:
for all edges (u,v) ∈ E:
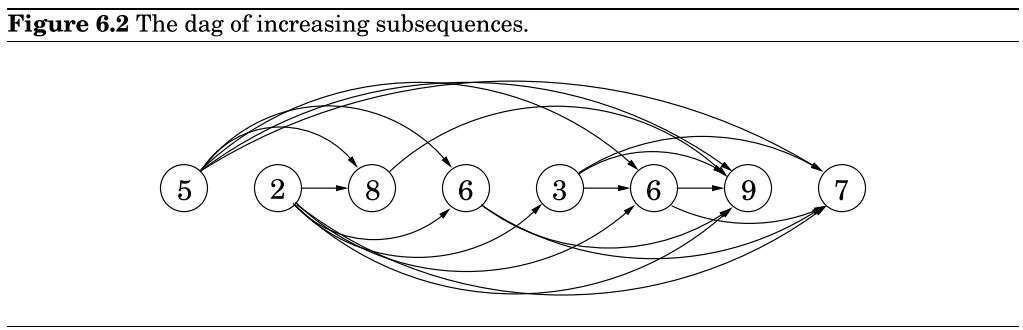
dist(v)=min(dist(u)+l(u,v))6.2 最长递增子序列
for j=1,2,...,n
L(j)=1+max{L(i):(i,j) ∈ E}
return L
//i为j的前驱,求反转图Gr即可6.3 编辑距离
将两个单词进行对齐,对齐代价为对应字母不相同的列数
6.3.1 一种动态规划的解
寻找两个字串: x[1...m],y[1...n] 之间的编辑距离 E(m,n) ,考虑字符串的前缀: x[1...i],y[1...j] 的编辑距离 E(i,j) 。
则:
E(i,j)=min{
1+E(i−1,j),1+E(i,j−1),diff(i,j)+E(i−1,j−1)}
for i=0,...,m:
E(i,0)=i
for j=0,...,n:
E(0,j)=j
for i=1,...,m:
for j=1,...,n:
E(i,j)=min{
1+E(i-1,j),1+E(i,j-1),diff(i,j)+E(i-1,j-1)}
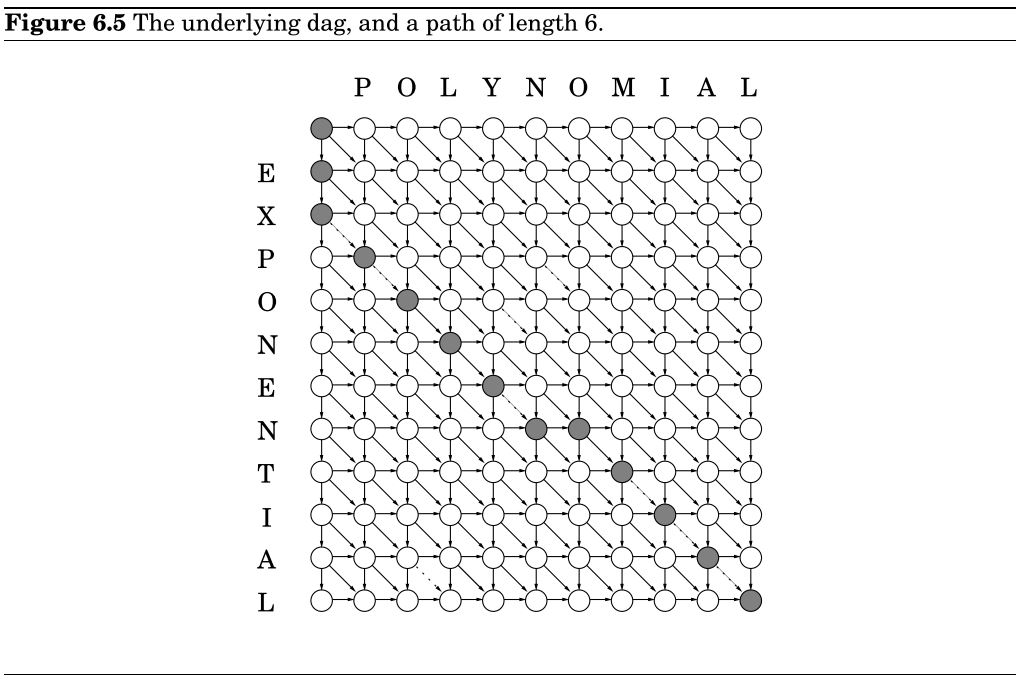
return E6.3.2 隐含的dag
每个动态规划都隐含着一个dag结构:每个节点表示一个子问题,每条边表示解决子问题时的先后约束。
除边 { (i−1,j−1)→(i,j):x[i]=y[j]} 为0外,其余边为0;问题转为求点 s=(0,0) 到点 t=(m,n) 的最短距离。
其中,为使 EXPONENTIAL 转为 POLYNOMIAL
- 向下表示删除
- 向右表示插入
向对角线表示匹配或替换
6.4 背包问题
- n件物品,W总重量的背包,复杂度 O(nW)
6.4.1 多副本背包问题
- Knapsack with repetition








 这篇博客深入探讨了动态规划在多种问题中的应用,包括最短路径问题、最长递增子序列、编辑距离、背包问题和矩阵链式相乘。通过详细阐述DAG的最短路径、编辑距离的动态规划解法、不同类型的背包问题以及旅行商问题,揭示了动态规划解决问题的内在dag结构和优化策略。此外,还讨论了树中的独立集问题。
这篇博客深入探讨了动态规划在多种问题中的应用,包括最短路径问题、最长递增子序列、编辑距离、背包问题和矩阵链式相乘。通过详细阐述DAG的最短路径、编辑距离的动态规划解法、不同类型的背包问题以及旅行商问题,揭示了动态规划解决问题的内在dag结构和优化策略。此外,还讨论了树中的独立集问题。
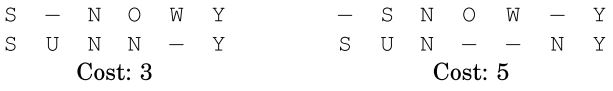
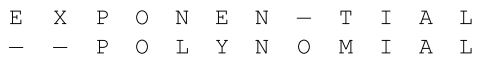
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 71
71

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








