二叉树——Treap树（平衡树）

什么是树形结构

树形结构是一层次的嵌套结构。一个树形结构的外层和内层有相似的结构，所以这种结构可以递归的表示。经典数据结构中的各种树状图是一种典型的树形结构：一棵树可以简单地表示为根、左子树、右子树。左子树、右子树又有自己的子树。

什么是二叉搜索树（Binary Search Tree）

每个元素有自己的键值，这些键值能比较大小。通常把键值放在BST的节点上。任意一个节点的键值，比它左子树的所有键值都大，比它右子树的所有键值都小——中序遍历就可以得到它的有序排列。

树形结构的作用——这里主要讲二叉搜索树

数组的搜索比较方便，可以直接用下标，但删除或者插入某些元素就比较麻烦。
链表与之相反，删除和插入元素很快，但查找很慢。
二叉排序树就既有链表的好处，也有数组的好处。
在处理大批量的动态的数据是比较有用。

Treap树

当给出一组序列，让我们给这组序列建立二叉搜索树的时候，如果给出的序列正好是按顺序递增或递减给出的，那我们建立的二叉搜索树就会退化成一种链状结构，也就失去了树形结构的意义。
像这样就属于退化后的二叉树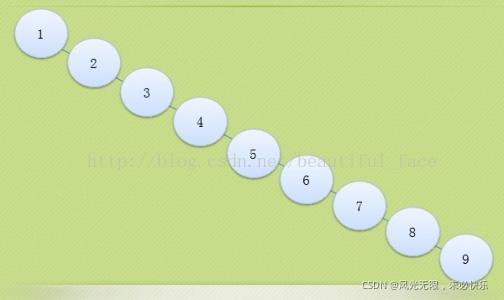
所以为了使二叉搜索树保持平衡，我们在二叉搜索树的基础上为它增加了一个优先级。对于键值来说，这是一个二叉搜索树；对于优先级来说，这是一个堆。堆的性质：在这棵树上，根的优先级最大。

那么怎么定义这个优先级呢？

这里我们用的使随机函数为节点随机分配的优先级，这样生成的树的形态也是随机的。这样虽然不能保证生成平衡二叉树，但是期望的插入、删除、查找的时间复杂度都是O（log2n）的。所以这里就牵扯到概率问题了，随机分配的优先级我们认为是形成了平衡二叉搜索树。

如可插入节点？

因为有优先级，当我们插入一个节点时，发现这个节点随机分配的优先级比根节点大，那么我们怎样把这个节点去放到根节点上呢？这里就用到了旋转技术——左旋、右旋（具体原理咱也想不到，只能说发明者nb）

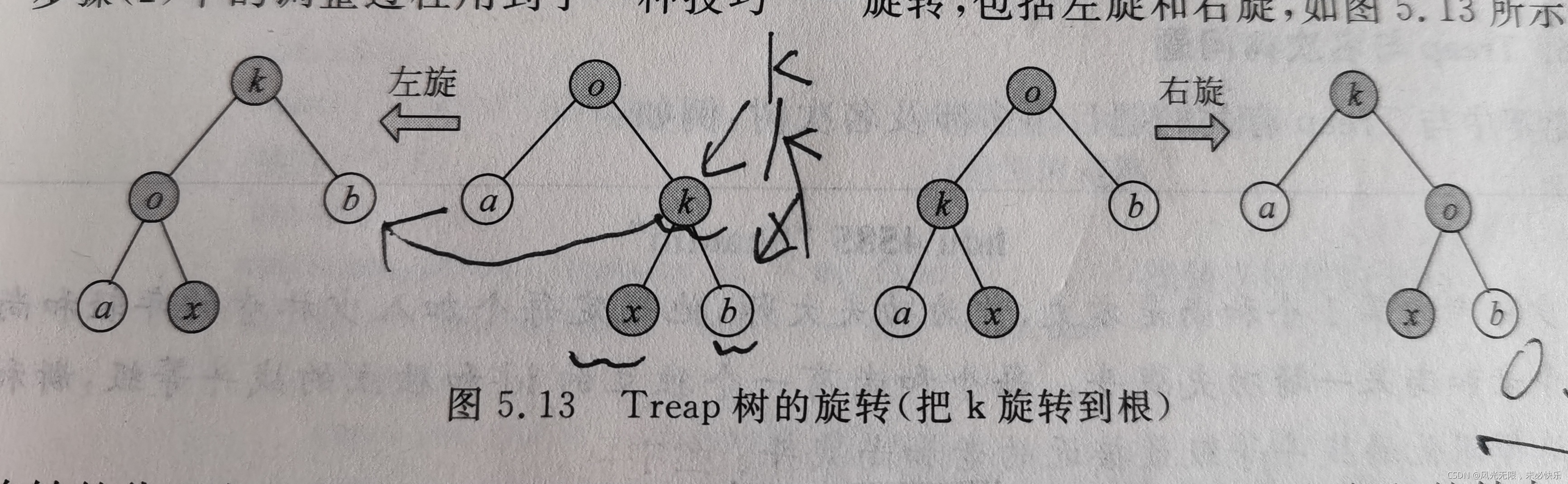
具体代码如下：

void rotate(node* &o,int d)//d=0，左旋；d=1，右旋
{
   
   
    node *k=o->son[1-d];
    o->son[1-d]=k->son[d];
    k->son[d]=o;
    o=k;
}

名次树

在Treap树的基础上增加了一个size和两个操作——查找名次、返回名次
下面用一个题目来具体处理Treap树与名次数：

hdu 4585 ShaoLin

题意：少林寺以孔府僧人而闻名。每年都有很多年轻人去少林寺，想在那里当和尚。少林大师主要以理解佛经的才华来评价年轻人，但战斗技巧也被考虑在内。‎
‎当一个年轻人通过所有的测试，并被宣布为少林的新和尚，将有一个战斗，作为欢迎的一部分。每个和尚都有独特的身份和独特的战斗等级，这些都是整数。新和尚必须与战斗等级最接近战斗等级的老和尚战斗。如果有两个老和尚满足这个条件，新和尚将采取的战斗等级低于他的一个。‎
‎大师是少林第一和尚，他的身份证是1，他的战斗等级是100万，他刚刚失去了战斗记录。但他仍然记得谁加入少林较早，谁加入较晚。请为他恢复战斗记录。‎

解题：对于这道题目来说，我们有多种方式来解决——set、map都可以用，并且理解起来也比较简单。这里就不再赘述，我们主要来看看如何用名次树来解决并了解名次树的基本操作。
名次数比Treap多的两个函数——1、kth（）查找第k大的元素；2、find（）查询元素x的名次。这两个功能的实现借助于size，size的值为以它为根的子树的节点总数量。
下面来说一说这棵树是怎么建的：
首先，对于二叉搜索树，我们得按战斗等级来划分吧，低于节点的放到左子树，大于节点的放到右子树。然后再看看随机分配的优先级是否满足堆的性质，不满足的话，我们就要进行旋转。最后建立的一定是一个二叉搜索树（就是可能不是平衡的，这里前面也说了，随机分配的优先级，在期望上它是平衡的）。有一点需要特别注意:虽然方丈的战斗等级是最高的（这一点是肯定的，方丈肯定最厉害）,但是他的size不一定是最大的，这里的名次与战斗等级以及人寺的时间都没关系。再强调一遍，size的定义是以它为根的子树的节点总数量。
接下来我们一点一点的分析代码：
1、结构体来定义树的节点——每一个节点需要包含size、rank（随机分配的优先级）、key（键值，即战斗等级）、两个儿子节点、按优先级排序的重载函数（这个函数让树满足堆的性质,如果不满足，就旋转）、比较函数cmp（用来判断节点是插入到左子树还是右子树）、更新size的函数（因为节点每进行一次操作，不管是左旋还是右旋，size都会改变）
代码如下：

struct node
{
   
   
   int size;
   int rank;
   int key;
   node *son[2];
   bool operator<(const node &a)const{
   
   return rank<a.rank;}
   int cmp(int x)const{
   
   if(x==key)