动态规划总结点睛

终于到这个专题啦 ~~~ 激动的搓手手！

一、基础知识

动态规划：Dynamic Programming (DP)，如果某一问题有很多重叠子问题，实验DP是最有效的

因此只要是 当前状态可以根据前面的状态推出来 的题型，就能用动归。

动态规划中每一个状态一定是由上一个状态推导出来的，这一点区分与贪心，贪心没有状态推导，而是从局部直接选最优、

贪心解决不了动态规划的问题。

01、花花讲解

要求:最优子结构可以通过把它分解成子问题，然后递归地找到子问题的最优解来得到最优解。重叠子问题子问题是重叠的，这样我们只能计算一次，并存储解决方案以备将来使用降低时间复杂度(指数到多项式)如果子问题不重叠->分治无后效应当一个子问题被用于求解一个更大的问题时，它的最优解不会改变

自上而下的:记忆化递归（从大到小）

自底向上:DP （从小到大）

使用DP的算法:

斐波那契序列

LCS

背包

弗洛伊德

沃沙尔bellman

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-n2gH09KX-1624203830729)(C:\Users\lh\AppData\Roaming\Typora\typora-user-images\image-20210620125840171.png)]

第一种问题

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-UvlOTyaj-1624203830735)(C:\Users\lh\AppData\Roaming\Typora\typora-user-images\image-20210620132135592.png)]

1、前缀和

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-HuhNBM4v-1624203830741)(C:\Users\lh\AppData\Roaming\Typora\typora-user-images\image-20210620132255046.png)]

2、爬楼梯

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-eUURX1j2-1624203830749)(C:\Users\lh\AppData\Roaming\Typora\typora-user-images\image-20210620132304314.png)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-39bohMae-1624203830751)(C:\Users\lh\AppData\Roaming\Typora\typora-user-images\image-20210620132542996.png)]

3、打家劫舍

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-39lBWtQh-1624203830752)(C:\Users\lh\AppData\Roaming\Typora\typora-user-images\image-20210620132324780.png)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-24yGeDIr-1624203830754)(C:\Users\lh\AppData\Roaming\Typora\typora-user-images\image-20210620132350512.png)]

4、使序列递增的最小交换次数

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-RyI6Dj7s-1624203830755)(C:\Users\lh\AppData\Roaming\Typora\typora-user-images\image-20210620132513639.png)]

5、多米诺和托米诺平铺

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-aRLCpSpE-1624203830758)(C:\Users\lh\AppData\Roaming\Typora\typora-user-images\image-20210620132528137.png)]

第二种问题

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-XCySdUVj-1624203830759)(C:\Users\lh\AppData\Roaming\Typora\typora-user-images\image-20210620133111881.png)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-HhqyjJJi-1624203830760)(C:\Users\lh\AppData\Roaming\Typora\typora-user-images\image-20210620133121348.png)]

1、不同路径

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-dzmWUvfE-1624203830769)(C:\Users\lh\AppData\Roaming\Typora\typora-user-images\image-20210620133134412.png)]

*********************************************************************************************************************************************

1、解题步骤

状态转移公式是很重要的，但是DP不仅仅只有递推公式。

动态规划五部曲：

• 确定 dp 数组（dp table）以及下标的含义
• 确定递推公式
• dp数组如何初始化
• 确定遍历顺序
• 举例推导dp数组

注意：是先确定地推公式，在考虑初始化。因为某些情况下，是递推公式决定了要如何初始化。

​ 这里的5个步骤，都必须清楚明了才能真正理解DP的整个过程哦~切忌仅把目光放在递推公式上。

2、DP 应该如何 debug

​ 找问题的最好方式就是把dp数组打印出来，看看究竟是不是按照自己思路推导的！所以要关注 dp 数组！！！

遇到问题时，其实可以自己先思考这三个问题：

• 这道题目我举例推导状态转移公式了么？
• 我打印dp数组的日志了么？
• 打印出来了dp数组和我想的一样么？

要清楚自己是哪里不明白：

• 是状态转移不明白，
• 还是实现代码不知道该怎么写，
• 还是不理解遍历dp数组的顺序。

3、DP 主要题型

• 经典题目
• 背包问题
• 打家劫舍问题
• 股票问题
• 子序列问题

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-j3QGEfh6-1624203830770)(C:\Users\lh\AppData\Roaming\Typora\typora-user-images\image-20210610184012519.png)]

3.1 背包问题理论和原理

​ 主要掌握 01 背包和完全背包，最多再来一个 多重背包 就够用了，力扣上连多重背包的问题都没有~

1、二维 01背包

有N件物品，和一个能背重量为W的背包，第 i 件物品的重量是 weight[i]，得到的价值为 value[i]，每件物品只能用一次，求解将哪些物品装入背包里的物品价值总和最大。

例题：假设 背包的最大重量为 4，物品如表中所示：

解法一：暴力搜素，回溯法

​ 每件物品的状态只有两个，取 或者不取，使用回溯搜索出所有的情况，时间复杂度为 O(2^n)，n 代表物品数量

解法二：动态规划

​ 对回溯法的优化。

动态规划五部曲：

• 1、确定dp数组以及下标的含义

  • dp[i] [j] 表示从下标为从0 到 i 个物品里任意取，放进容量为 j 的背包，价值总和最大是多少。
  • i 对应物品，表示从 0 到 i 个物品中 任意取，
  • j 对应背包所能承受的重量

• 2、确定递推公式，即状态转移方程

  • 有两个方向可以推出来 dp[i] [j]，也就是对于第 i 个物品，有两种状态，取 或者是 不取，所以需要有判断条件

  • 如果不取：由 dp[i - 1] [j] 推出，即背包容量为 j，里面不放物品 i 的最大价值，也就是当 背包的 容量 j 小于 物品 i 的重量时 ，此时dp[i] [j]就是dp[i - 1] [j]

  • 如果取： 由 dp[i - 1] [j - weight[i]] 推出，也就是当 背包的 容量 j 大于或者等于 物品 i 的重量时 ，dp[i - 1] [j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值，

    那么 dp[i - 1] [j - weight[i]] + value[i] （物品i的价值） ，就是背包放物品i得到的最大价值。

  • 所以递推公式：dp[i] [j] = max(dp[i - 1] [j], dp[i - 1] [j - weight[i]] + value[i]);

• 3、dp 数组的初始化

  • 两个方向，一个是 i = 0 时，一个是 j = 0 时

  • 对于 j = 0，在初始化 dp 数组的时候直接初始化，因为当背包所能承受最大重量为0时，背包价值只能是 0。

  • 对于 i = 0，要使用倒序遍历，用 for 循环，j 从后往前遍历；因为如果使用 正序遍历，物品 0 就会被重复加入多次。

  • 注意这里容易出错，一定要是倒序遍历，保证物品0只被放入一次，这一点对 01背包 很重要。经过初始化之后， dp 数组的第一行和第一列就完成了初始化。

  • 对于 dp 数组中的其他数组，如果题目中没有负数的价值，可以直接初始化为 0，

    如果出现了负数的价值，则需要将其初始化为 负无穷 INT_MIN

Attention：初始化的时候可以不加dp[0] [j-weight[0]]，就算只有value[0]也可以，但是加上是为了 与 滚动数组的写法相呼应。

• 4、确定遍历顺序
  • 本题遍历有两个维度：一个是物品，一个是背包重量。就需要考虑先遍历谁了，事实证明，先遍历物品更容易理解一些。
  • 那么理解一下，为什么两个方向都是可以的呢?
    • 要理解一下递归的本质和递推的方向。
    • 从递归公式中可以看出 dp[i] [j]是靠dp[i-1] [j]和dp[i - 1] [j - weight[i]]推导出来的。
    • dp[i-1] [j]和dp[i - 1] [j - weight[i]] 都在 dp[i] [j] 的正左方向 和正上方向，那么先向正上方走，亦或是先向正右方走是一样的。

// 第一种 先遍历物品，然后遍历背包重量
// weight数组的大小 就是物品个数
for(int i = 1; i < weight.size(); i++) { // 遍历物品
  for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量 
    if (j < weight[i]) dp[i][j] = dp[i - 1][j]; // 这个是为了展现dp数组里元素的变化
    else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
    
  }
}


// 先遍历物品，然后遍历背包重量 也可以写成如下的方式：
// 这两种方式打印出的 dp 数组是不同的，第二种遍历方式得到的左下角元素为 0 其实空出来的 0 ，是用不上的。
// 第二种 遍历过程
for(int i = 1; i < weight.size(); i++) { // 遍历物品
    for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
        if (j - weight[i] >= 0) {
            dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
        }
    }
}

// 第三种 先遍历背包重量，然后遍历物品
// weight数组的大小 就是物品个数
for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
  for(int i = 1; i < weight.size(); i++) { // 遍历物品
    if (j < weight[i]) dp[i][j] = dp[i - 1][j];
    else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
  }
}

// 完整代码

void test_2_wei_bag_problem1()
{
	vector<int> weight = { 1, 3, 4 };		// 物品重量
	vector<int> value = { 15, 20, 30 };	// 物品价值
	int object = 3;						// 物品数量
	int bagWeight = 4;					// 背包容量

	// 定义 dp 数组
	vector<vector<int>> dp(object, vector<int>(bagWeight + 1, 0));

	// 初始化
	// j = 0 的情况就是 0，相当于在定义时就已经初始化了
	// 易出错点一：：终止条件处
	for (int j = bagWeight; j >= weight[0]; j--)
	{
		// 这里初始化有两种写法，都可以的，第二种是为了呼应接下来学习的滚动数组
		//dp[0][j] = value[0];
		 dp[0][j] = value[0] + dp[0][j - weight[0]];
	}

	// 遍历 dp 数组
	for (int i = 1; i < object; i++)	// 遍历物品
	{
		for (int j = 1; j <= bagWeight; j++)	// 遍历背包容量
		{
			// 易出错点二：：终止条件处
			// // 判断的方法一：这里的判断条件忘记了！！！！！！！！
			// 常错项 max 的第二个元素，value[i] + dp[j - weight[i]]，这个 dp 老是写错。
			if (j < weight[i])
				dp[i][j] = dp[i - 1][j];
			else
				dp[i][j] = max(dp[i - 1][j], value[i] + dp[i - 1][j - weight[i]]);

			// // 判断的方法二：
			//if (j - weight[i] >= 0) 
			//	dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

			cout << dp[i][j] << " ";
		}
		cout << endl;
	}
}

int main()
{
	test_2_wei_bag_problem1();
	return 0;
}

2、一维 01背包 滚动数组

对于背包问题，其状态都是可以压缩的，也就是把二维变成一维，

也就是上一层可以重复利用，将上一层直接拷贝到当前层，这就是滚动数组的由来。

将 dp[i] [j] 压缩为 dp[j]。dp[i] [j] 的含义是 从 0 到 i 个物品中任意抽取，并放进容量为 j 的背包中，其价值总和最大为 dp[j] 。

动态规划五部曲：

• 1、确定 dp 数组及其下标的含义
  • 在一维 dp 数组中，dp[j] 表示：容量为 j 的背包，所背的物品价值可以最大为 dp[j]
• 2、一维 dp 数组的递推公式
  • dp[j]有两个选择，一个是取自己dp[j]，一个是取dp[j - weight[i]] + value[i]，取两者中的最大值。
• 3、一维 dp 数组的初始化
  • 如果题目给的价值都是正整数，那么就将 dp[0] = 0，其余元素也置位 0，
  • 如果题目给的价值存在负数，那么就将 dp[0] = 0，其余元素置位 无穷小，INT_MIN
• 4、确定遍历顺序
  • 注意这里有不同哦！
  • 第一：在二维 dp 遍历的时候，背包容量的大小是从小到大，在一维 dp 遍历时，背包容量是从大到小，也就是倒叙。why？？？
    • 倒叙遍历，只为了保证物品 i 只被放入一次。注意这里有一个前提是，在初始化的时候， dp 数组都被初始化为 0。
    • 所以说 从后往前遍历，每次取得的状态不会和之前取得的状态重合，这样每种物品就只取一次了。
  • 那么为什么二维 dp 数组的时候，不用倒叙呢？
    • 因为对于二维 dp ，每个dp[i] [j] 都是从上一层计算而来的，本层的不会被覆盖。
  • 第二：二维 dp 遍历时 背包容量 和 物品 谁先谁后都可以，但是！对于一位 dp ，一！定！是！先！物品！，再！背包容量！

// 完整代码
void test_1_wei_bag_problem()
{
	vector<int> weight = { 1, 3, 4 };
	vector<int> value = { 15, 20, 30 };
	int object = weight.size();
	int bagWeight = 4;

	// 初始化
	vector<int> dp(bagWeight + 1, 0);
	for (int i = 0; i < object; i++)		// 遍历物品
	{
		for (int j = bagWeight; j >= weight[i]; j--)		// 遍历背包容量
		{
			// 常错项 max 的第二个元素，value[i] + dp[j - weight[i]]，这个 dp 老是写错。
			dp[j] = max(dp[j], value[i] + dp[j - weight[i]]);
			
		}
		// 打印日志
		for (int k = 0; k < dp.size(); k++)
		{
			cout << dp[k] << " ";
		}
		cout << endl;
	}
}

int main()
{
	test_1_wei_bag_problem();
}

3、完全背包

有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品都有无限个（也就是可以放入背包多次），求解将哪些物品装入背包里物品价值总和最大。

完全背包和 01 背包唯一不同的就是，每种物品有无限件。

• 要点一：完全背包的一维 dp 数组内层循环遍历顺序是从小到大，

  • （注意 01背包的一维 dp 数组内层循环为倒叙，即遍历顺序是从大到小）
  • 因为 01背包 是为了保证每个物品仅被添加一次，而完全背包的物品是可以添加多次的。

• 要点二：为什么物品遍历在外层，背包容量遍历在内层？

  • 在 01背包 中 二维 dp 数组的两个 for 循环顺序可以颠倒，但是一维 dp 数组的两个for循环一定不能换遍历顺序的，外层是物品遍历，内层是背包容量遍历。
  • 在 完全背包中，对于 一维 dp 数组 来说，其实两个for循环嵌套的顺序同样是无所谓的。也就是两个 for 循环的先后顺序，都不影响计算 dp[j] 所需要的的值（也就是下标 j 之前所对应的 dp[j] ）

• 对于 纯完全背包 问题，不用区分是求组合数还是求排列数，

  因为纯完全背包是 求解将哪些物品装入背包里物品价值总和最大，此时先遍历物品还是先遍历物品是一样的

• 但是利用完全背包求解有多少种方式的时候，就要区别是组合数还是排列数了

  要分清楚是求组合数还是求排列数

  求组合数：外层遍历物品，内层遍历背包，都是正序从小到大进行

  求排列数：外层遍历背包，内层遍历物品，都是正序从小到大进行

// 完整代码
void test_CompletePack()
{
	vector<int> weight{1, 3, 4};
	vector<int> value{15, 20, 30};
	int object = weight.size();
	int bagWeight = 4;
	
	// 初始化
	vector<int> dp(bagWeight + 1, 0);
	
	// 遍历方式一：外层遍历物品，内层遍历背包容量
	for(int i = 0; i < object; i++)
	{
		// 注意这里终止条件是有个等号的
		for(int j = weight[i]; j <= bagWeight; j++)
		{
			// 常错项 max 的第二个元素，value[i] + dp[j - weight[i]]，这个 dp 老是写错。
			dp[j] = max(dp[j], value[i] + dp[j - weight[i]]);
		}
		// 打印日志
		for (int k = 0; k < dp.size(); k++)
        {
            cout << dp[k] << " ";
        }
        cout << endl;
	}
	
	 遍历方式二：外层遍历背包容量，内层遍历物品
	//for (int j = 0; j <= bagWeight; j++)
	//{
	//	for (int i = 0; i < object; i++)
	//	{
	//		if (j - weight[i] >= 0)
	//		{
	//			// 常错项 max 的第二个元素，value[i] + dp[j - weight[i]]，这个 dp 老是写错。
	//			dp[j] = max(dp[j], value[i] + dp[j - weight[i]]);
	//		}
	//	}
	//	// 打印日志
	//	for (int k = 0; k < dp.size(); k++)
	//	{
	//		cout << dp[k] << " ";
	//	}
	//	cout << endl;
	//}
}

int main()
{
	test_CompletePack();
}

4、多重背包

有N种物品和一个容量为V 的背包。第i种物品最多有Mi件可用，每件耗费的空间是Ci ，价值是Wi 。求解将哪些物品装入背包可使这些物品的耗费的空间 总和不超过背包容量，且价值总和最大。

• 多重背包和01背包是非常像的：
  • 因为每件物品最多有Mi件可用，把Mi件摊开，其实就是一个01背包问题了。

二、做题记录

1、常规题型

第509题 斐波那契数

动态规划五部曲：

• 1、确定dp数组以及下标的含义
  • dp[i] 定义为：第 i 个数的斐波那契数值是 dp[i]
• 2、确定递归公式
  • dp[i] = dp[i - 1] + dp[i - 2]
• 3、dp数组如何初始化
  • dp[0] = 0;
  • dp[1] = 1;
• 4、确定遍历顺序
  • 因为 dp[i] 依赖于 dp[i - 1] 和 dp [i - 2]，所以遍历顺序肯定是从前向后
• 5、举例推导dp数组
  • 举例当 N = 10，dp 数组应该是： 0 1 1 2 3 5 8 13 21 34 55

如果代码写出来不对，就把dp数组打印出来，看看和我们推导的数列是不是一致。

第70题 爬楼梯

规律描述：

爬到第一层楼梯有一种方法，爬到第二层楼梯有两种方法

那么爬到第三层的方法可以由第一层和第二层的状态推导出来：

​ 第一层楼梯再夸两步就到第三层

​ 第二层楼梯再夸一步就到第三层

动态规划五部曲：

• 1、确定 dp 数组以及下标的含义
  • dp[i] 爬到第 i 层楼梯，有dp[i] 种方法
• 2、确定递推公式
  • dp[i - 1]，表示上到 i-1 层，有 dp[i-1] 种方法，那么再跳一个台阶就是到了第 i 层
  • dp[i - 2]，表示上到 i-2 层，有 dp[i-2] 种方法，那么再跳两个台阶就是到了第 i 层
  • 所以 dp[i] = dp[i - 1] + dp[i - 2]
  • 在推导 dp[i] 的时候，一定要时刻想着 dp[i] 的定义，否则很容易跑偏的。这就体现了确定 dp 数组以及其下标的含义的重要性
• 3、dp 数组如何初始化
  • dp[1] = 1
  • dp[2] = 2
  • 不去争论 dp[0]，直接初始化 dp[1] 和 dp[2] ，然后推导直接从 i = 3 开始。
• 4、确定遍历顺序
  • 遍历顺序 从前向后
• 5、举例推导数组
  • 当 n = 5 时， dp 数组为 注意 下标从 1 开始！！！ 1 2 3 5 8

第62题 不同路径

​ 递推公式 dp[i] [j] = dp[i - 1] [j] + dp[i] [j - 1]： dp[i] [j]定义 ：表示从（0 ，0）出发，到(i, j) 有dp[i] [j]条不同的路径

第343题 整数拆分

​ 递推公式：dp[i] = max(dp[i], max(i * (j - i), j * dp[i - j])) dp[i] 分拆数字 i，可以得到的最大乘积为 dp[i]

第96题 不同的BST

​ 递推公式： dp[i] = dp[i] + dp[j - 1]*dp[i-j] dp[j-1]是以 j-1 为头结点左子树节点数量， dp[i-j]是以j为头结点右子树节点数量

2、背包问题

第416题 分割等和子集

转化为 01背包问题：

确定以下问题：

• 1、背包的体积为 sum/2， 物品的个数就是 nums数组的个数，背包中的每一个元素不可以重复放入。
• 2、物品的价值就是 nums 数组中每个元素（物品）的大小
• 3、物品的重量就是 nums 数组中每个元素（物品）的大小
• 4、背包中要放入的 物品重量 为 元素的数值，价值 为 元素的数值
• 5、是否能分割成两个元素和相等的子集 转换为 当背包容量为 sum/2 时所装的物品的最大价值能否是 sum/2
• 6、如果 dp[i] == i
  • 说明集合中的子集总和正好可以凑成总和 i，
  • 也就是背包容量 为 i 时，所装物品的最大价值为 i，或者不考虑价值维度，将其理解为 背包容量为 i 时，判断能否将其装满，也就是 dp[i] = i，i 就表示背包的容量
  • 也就是可以将这个数组分割成两个子集，使得两个子集的元素和相等，这正是我们要求的。

动态规划五部曲：

• 1、确定dp数组以及下标的含义

  • dp[j] 表示容量为j的背包，所背的物品价值最大可以为 dp[j]

• 2、确定递归公式

  • 首先记着01背包的递推公式：dp[j] = max(dp[j], value[i] + dp[j - weight[i]])
  • 将上式转换一下： dp[j] = max(dp[j], nums[i] + dp[j - nums[i]])

• 3、dp数组初始化

  • 与 01背包一样，当j=0,也就是背包容量为0时，dp[0] = 0;
  • 且本题中数组元素均为正整数，因此初始化为 0 是没问题的，如果有负数，那就需要初始化为负无穷

• 4、确定遍历顺序

  • 先遍历物品，再遍历背包容量
  • 因为 01背包的一维 dp 数组，遍历顺序是固定的，只能是先物品，再背包容量

第698题 划分为k个相等的子集

​ 放在回溯的专题中了

第473题 火柴拼正方形

第1049题 最后一块石头的重量

转化为 01背包问题：

确定以下问题：

• 1、背包的体积为 sum/2， 物品的个数就是 stones 数组的个数，背包中的每一个元素不可以重复放入。
• 2、物品的价值就是 stones 数组中每个元素（物品）的大小
• 3、物品的重量就是 stones 数组中每个元素（物品）的大小
• 4、背包中要放入的 物品重量 为 元素的数值，价值 为 元素的数值
• 5、这道题最后返回的是 sum - 2 * target。也就是最后剩的最小值，除了返回值的处理，其余的跟上一个非常类似，先把stones分割成两个和相等的子集，是否能分割成两个元素和相等的子集 转换为 当背包容量为 sum/2 时所装的物品的最大价值能否是 sum/2
• 6、如果 dp[i] == i
  • 说明集合中的子集总和正好可以凑成总和 i，
  • 也就是背包容量 为 i 时，所装物品的最大价值为 i， 或者不考虑价值维度，将其理解为 背包容量为 i 时，判断能否将其装满，也就是 dp[i] = i，i 就表示背包的容量
  • 也就是可以将这个数组分割成两个子集，使得两个子集的元素和相等，这正是我们要求的。
  • 背包容量为 target 对应的最大价值如果能等于 target 就说明找到了这个数组。自己列了一遍 dp 数组，好像明白了为什么要这么写，因为容量最大对应的价值才会是最大的嘛~~~

这道题与第416题的思路很相似，主要的不同分有以下几个：

• dp[j] 表示容量为 j 的背包，所装物品的最大价值为 dp[j]
• 物品是个数为 stones.size(), stones数组中的每个元素既是物品重量，又是物品价值
• 理解一下，最后return时 为什么取这个dp[target]，此时的 dp[target]

动态规划五部曲：

• 1、确定dp数组以及下标的含义

  • dp[j] 表示容量为j的背包，所背的物品价值最大可以为 dp[j]

• 2、确定递归公式

  • 首先记着01背包的递推公式：dp[j] = max(dp[j], value[i] + dp[j - weight[i]])
  • 将上式转换一下： dp[j] = max(dp[j], nums[i] + dp[j - nums[i]])

• 3、dp数组初始化

  • 与 01背包一样，当j=0,也就是背包容量为0时，dp[0] = 0;
  • 且本题中数组元素均为正整数，因此初始化为 0 是没问题的，如果有负数，那就需要初始化为负无穷

• 4、确定遍历顺序

  • 先遍历物品，再遍历背包容量
  • 因为 01背包的一维 dp 数组，遍历顺序是固定的，只能是先物品，再背包容量

第494题 目标和

分析：

• 式一：left - right = target; 式二： left + right = sum

• 式一 与 式二 相加可得 式三：2*left = target + sum

• 式三中 target 与 sum 都是已知且固定的，因此 left 可由此得出。

第一种解法：回溯法中的组合总和。

• 时间复杂度都是是O(2^n)级别，所以最后超时了。

• 为了加深自己的理解，自己写了一个版本，与 Carl的有差别，但是最后三个版本的都超时了

第二种解法：转换为 01背包问题

• 1、为什么是 01背包呢？

• 因为数组中的每个值只能用一次。

• 2、与之前的不同，之前都是求容量为 j 的背包可以装的最大价值，

  ​ 而本题是 表示容量为 j 的背包装满有 dp[j] 种方法。

• 3、 复杂度分析

  • 时间复杂度O(n * m)，n为正数个数，m为背包容量

• 空间复杂度：O(m) m为背包容量

• 4、本题中是求装满有几种方法，这其实还是回归的组合

  • 1、确定 dp 数组以及下标的含义
    dp[j] 表示容量为 j 的背包装满，有 dp[j] 种方法
  • 2、确定递推公式
    求组合类的问题都是类似于这种，其实就是把这些方法加起来就可以了。
    几乎所有的背包解决排列组合问题，都是用这个递推公式
    记住：在求装满背包有几种方法的情况下，递推公式就是这个，后面也会用到：
    dp[j] = dp[j] + dp[j - nums[i]]
  • 3、dp 数组如何初始化
    dp[0] = 1，dp[j] 其他下标对应的数值应该初始化为 0。
    寓意为：装满容量为0的背包，有1种方法，就是装 0 件物品
    注意这里可不能把 dp[0]初始化为 0，这样会导致所有的递归结果都将是0，
  • 4、确定遍历顺序
    nums 放在外循环， target 放在内循环， 且内循环倒叙
    这个与之前的 01背包问题相似

第474题 一和零

本题是等价为 01背包问题，只不过这个背包是有两个维度来决定的，一个是m, 一个是n

数组中不同长度的字符串就是不同大小的物品。

背包容量就是 m 和 n

自己写写 dp 数组有助于理解啊

动规五部曲：

• 1、确定 dp 数组以及下标的含义

  • dp[i] [j]：最多有 i 个 0 和 j 个 1 的 strs 的最大子集的大小为 dp[i] [j]

• 2、确定递推公式

  • dp[i] [j]可以由前一个strs里的字符串推导出来，strs里的字符串有zeroNum个0，oneNum个1。
  • 字符串的zeroNum和oneNum相当于物品的重量（weight[i]）
  • 字符串本身的个数相当于物品的价值（value[i]）
  • dp[i] [j] = max(dp[i] [j], dp[i - zeroNum] [j - oneNum] + 1);

• 3、dp 数组如何初始化

  • 01 背包的dp数组初始化为0即可

• 4、确定遍历顺序

  • 物品就是 strs 中的字符串，
  • 背包容量就是 m 和 n
  • 外层for循环遍历物品，内层for循环遍历背包容量，且内层是倒叙遍历

第279题 完全平方数

等价为 完全背包

本题等价为 完全背包问题

背包的最大容量为 n

物品 就是 完全平方数，第i个物品对应的重量也是 i，但是本题是要 ii，所以物品每次从 i 开始，到 n 为止，每次判断用 ii

问：装满背包所用物品的最小个数是多少个？

dp数组定义：dp[i] 表示背包容量为 i 时，装满背包所用物品的最小个数是 dp[i] 个

dp数组初始化：dp[0] = 1，其余的为 INT_MAX

递推公式 ：dp[i] = min(dp[i], dp[i - coins[j]] + 1)

遍历顺序：因为是在装满背包的情况下所用物品的最小个数，因此遍历顺序是无所谓的

因为是完全背包，所以遍历时均为正序遍历

// // 错误1：dp[0] = 0 没有初始化

// // 错误2：外层遍历物品时的终止条件是 i*i<n，我刚刚忘记乘上i了

// // 错误3：内层的防止溢出有两个，一个是对于下标，要求 j-ii 大于或者等于 0，还有一个是 dp[j-ii] != INT_MAX

// // 注意 if (j - i * i >= 0 && dp[j - i * i ] != INT_MAX) 的等于号 ，刚刚我没有加等于号

关于排列 & 组合

• 在排列问题中，面试时可以考察：两个for循环的嵌套顺序，为什么target放外面，nums放里面。

• 因为这是一个组合问题，如果不这样的话，物品的顺序就是从 i 开始，这样就不会包括和相等但是顺序不同的了

• 对于 纯完全背包 问题，不用区分是求组合数还是求排列数，

• 因为纯完全背包是求解 将哪些物品装入背包里物品价值总和最大，此时先遍历物品还是先遍历物品是一样的

• 但是利用完全背包求解有多少种方式的时候，就要区别是组合数还是排列数了

• 要分清楚是求组合数还是求排列数

  • 求组合数：外层遍历物品，内层遍历背包，都是正序从小到大进行
  • 求排列数：外层遍历背包，内层遍历物品，都是正序从小到大进行

第322题 零钱兑换

本题属于本题属于完全背包问题：

本题中的dp数组的下标和含义要依据题意来变一下

dp[j] 凑足总金额为 j 所需铅笔的最少个数为 dp[j]

求最小就需要将除了第一个元素之外的值 初始化为 INT_MAX，

同时，因为有了INT_MAX所以要多一句 if 判断来防止溢出。

动规五部曲：

1、确定dp数组及其下标含义

dp[j] 凑足总金额为 j 所需铅笔的最少个数为 dp[j]

2、确定递推公式

①：考虑coins[i]时: dp[j] = dp[j]

②：不考虑coins[i]时：dp[j] = 1 + dp[j - coins[i]]

取两者中的最小值：dp = min(dp[j], 1 + dp[j - coins[i]])

3、dp数组初始化

j = 0 时，对应的 dp[j] = 0

j 为其他下标时，dp[j] = INY_MAX，将其初始化为一个最大数，为了避免在 min() 求最小值比较的过程中被初始值覆盖

4、确定遍历顺序

本题不强调物品与背包的遍历顺序，两种都可以的

此处采用先遍历物品，再遍历背包容量，内层循环用正序问题：

本题中的 dp数组的下标 和含义要依据题意来变一下

dp[j] 凑足总金额为 j 所需铅笔的最少个数为 dp[j]

求最小就需要将除了第一个元素之外的值 初始化为 INT_MAX，

同时，因为有了INT_MAX所以要多一句 if 判断来防止溢出。

动规五部曲：

• 1、确定dp数组及其下标含义

  • dp[j] 凑足总金额为 j 所需铅笔的最少个数为 dp[j]

• 2、确定递推公式

  • ①：考虑coins[i]时: dp[j] = dp[j]
  • ②：不考虑coins[i]时：dp[j] = 1 + dp[j - coins[i]]
  • 取两者中的最小值：dp = min(dp[j], 1 + dp[j - coins[i]])

• 3、dp数组初始化

  • j = 0 时，对应的 dp[j] = 0
  • j 为其他下标时，dp[j] = INY_MAX，将其初始化为一个最大数，为了避免在 min() 求最小值比较的过程中被初始值覆盖

• 4、确定遍历顺序

  • 本题不强调物品与背包的遍历顺序，两种都可以的
  • 此处采用先遍历物品，再遍历背包容量，内层循环用正序

第518题 零钱兑换V2

本题等价为 完全背包 问题

组合数：先遍历物品，在遍历背包

第一：转换为 完全背包来理解 : 两个都是正序，从小到大进行遍历即可

第二：求组合数 ： 先遍历物品，在遍历背包

第三：求装满背包有几种方法 ： dp[i] = dp[i] + dp[j - nums[i]]

动规五部曲：

• 1、确定dp数组及其下标含义

  • dp[j] 凑足总金额为 j 时，有 dp[j] 种方式可以凑成总金额

• 2、确定递推公式

  • 求组合类的问题都是类似于这种，其实就是把这些方法加起来就可以了。
  • 494题 目标和 也是这样
  • dp[j] = dp[j] + dp[j - coins[i]]

• 3、dp数组初始化

  • j = 0 时，对应的 dp[j] = 1
  • 表示 amount = 0时，有 1 种方式可以凑成总金额

• 4、确定遍历顺序

  • 求组合数
  • 此处采用先遍历物品，再遍历背包容量，都用正序

3、打家劫舍

第198题 打家劫舍

打家劫舍是 dp 解决的经典问题。

• 1、确定 dp 数组及其下标的含义

  • dp[i] 表示考虑下标为 i 的房屋，最多可以偷窃的金额为 dp[i]

• 2、确定递推公式

  • dp[i] = max(dp[i - 1], nums[i] + dp[i - 2])

• 3、dp 数组初始化

  • dp[0] = nums[0];
  • dp[1] = max(nums[0], nums[1])；

• 4、确定遍历顺序

  • 遍历顺序肯定是从前后

第213题 打家劫舍V2

围城了环，那么就有三种情况

• 情况一：将首元素和尾元素都不考虑，仅考虑中间，
• 情况二：考虑首元素，但是不考虑尾元素
• 情况三：考虑尾元素，但是不考虑首元素

情况二和情况三已经包括了情况一，所以只需考虑后面两种情况即可，

很巧妙的解决了成环问题

第337题 打家劫舍V3

树的遍历有四种，本题一定是要后序遍历的，因为需要通过递归函数返回值来考虑的返回值，来计算下一步的结果

无需重新定义 递归函数，本题中给的函数已经符合写递归的条件，直接写就好了嘛

（1）方法一：暴力递归

n 表示节点个数

• 时间复杂度：O(n^2) 这个时间复杂度不太标准，也不容易准确化，例如越往下的节点重复计算次数就越多

• 空间复杂度：O(n) 算上递推系统栈的空间

• 计算了root的四个孙子（左右孩子的孩子）为头结点的子树的情况，又计算了root的左右孩子为头结点的子树的情况，计算左右孩子的时候其实又把孙子计算了一遍。

（2）方法二：记忆化递推

• 时间复杂度：O(n)

• 空间复杂度：O(n) 算上递推系统栈的空间

• 要点就是使用一个 map 把计算过的结果保存一下，这样就可以对方法一进行优化，如果计算过孙子，那么计算孩子的时候可以重复用孙子的结果

（3）方法三：动态规划

• 时间复杂度：O(n) 每个节点只遍历了一次
• 空间复杂度：O(n) 算上递推系统栈的空间

上面两种方法对一个节点 偷与不偷得到的最大金钱都没有做记录，而是需要实时计算的，

而动态规划其实就是使用状态转移容器来记录状态的变化，这里可以使用一个长度为2的数组

记录当前节点偷与不偷所得到的最大金钱

本题可以称为 树形dp 的入门题目，也就是在树上进行状态转移，递归三部曲 + 动规五部曲

• 1、确定递归参数和返回值类型
  • 因为是求当前节点 偷 与 不偷 的两个状态所得到的金钱，那么返回值就是一个长度为 2 的数组，这个就是 dp 数组
  • dp 数组以及下标的含义：
    • dp[0] 记录不偷该节点所得到的最大金钱 ，下标0，不偷
    • dp[1] 记录偷该节点所得最大金钱 ， 下标1，偷
  • 如果疑惑长度为2的数组怎么标记树中每个节点的状态呢？ 别忘啦！在递归的过程中，系统栈会保存每一层递归的参数
• 2、确定终止条件
  • 如果遇到空节点，就返回 vector{0, 0}
  • 这一步也相当于 dp 数组的初始化
• 3、确定遍历顺序
  • 首先明确是后序递归遍历，通过递归函数的返回值来做下一步的计算
  • 通过递归左节点，得到左节点 偷 与 不偷 的金钱
  • 通过递归右节点，得到右节点 偷 与 不偷 的金钱
• 4、确定单层递归逻辑（左–右--中）
  • 如果偷当前节点，那么左右孩子就不能偷
    • val1 = cur->val + left[0] + right[0];
  • 如果不偷当前节点，那么左右孩子就可以偷，至于偷还是不偷，就看偷后的大，还是不偷的大
    • val2 = max(left[0], left[1]) + max(right[0], right[1]);
  • 最后当前节点的状态就是
    • {val1，val2} 即 {不偷当前节点得到的最大金钱，偷当前节点得到的最大金钱}

4、股票问题

第121题 只买卖一次的最大利润

三种解题思路：

1、暴力解法

2、贪心解法

3、动规解法

• 时间复杂度：O(n)
• 空间复杂度：O(n)

动态规划五部曲：

• 1、确定 dp 数组以及下标的含义

  • dp[i] [0] 表示第 i 天持有股票所得现金，注意这个现金是有可能为负数的
  • dp[i] [1] 表示第 i 天不持有股票所得现金，

  ​ 注意：：这里的持有或者不持有，并不代表是否买入，持有也可能是昨天就买入了，今天保持持有状态，但是今天并不买入

• 2、确定递推公式

  • 对于 dp[i] [0]，可以由两个状态推出来
    • 第 i-1 天就持有股票，那么就保持现状，所得现金就是昨天持有股票时的所得现金，即 dp
    • 第 i 天买入股票，那么所得现金就是买入今天的股票后的所得现金 -prices[0]
    • 那么最终的 dp[i] [0] = max(dp[i-1] [0], -prices[0]) （dp[i-1] [1] - prices[i] (我的感觉)）
  • 对于 dp[i] [0]，也可以由两个状态推出来
    • 第 i-1 天本身就不持有股票，那么就保持现状，所得现金就是昨天不持有股票的所得现金，即 dp
    • 第 i 天卖出股票，那么所得现金就是按照今天股票价格卖出后所得现金，即 dp[i-1] [0] + prices[i]
    • 那么最终的 dp[i] [1] = max(dp[i-1], dp[i-1] [0] + prices[i])

• 3、dp 数组初始化

  • 由递推公式可以看出其基础都是从 dp[0] [0] 和 dp[0] [1] 推导出来的
    • dp[0] [0] = -prices[0]
    • dp[0] [1] = 0

• 4、确定遍历顺序

  • 一定是从前往后遍历，因为 dp[i] 是由 dp[i-1] 推导而来的

将动规法用滚动数组做状态压缩，可以优化空间

• 时间复杂度：O(n)
• 空间复杂度：O(1)

第123题 最多可以买 2 次买卖股票V3

动规五部曲：

• 1、确定 dp 数组以及下标的含义

  • dp[i] [j] ：i 表示第 i 天， j 表示 0-4 的五种状态，整体表示，第 i 天在状态 j 下所剩的最大现金
  • 一天可能有的状态有以下五种：
    • 0 ：不做任何操作
    • 1 ：第一次买入
    • 2 ：第一次卖出
    • 3 ：第二次买入
    • 4 ：第二次卖出

• 2、确定递推公式

  • dp[i] [1] = max(dp[i - 1] [1], dp[i - 1] [0] - prices[i])
    • 操作一：第 i 天没有操作，而是沿用前一天买入的状态dp[i] [1] = dp[i - 1] [1]
    • 操作一：第 i 天买入股票了，那么dp[i] [1] = dp[i-1] [0] - prices[i]
  • dp[i] [2] = max(dp[i - 1] [2], dp[i - 1] [1] + prices[i])
    • 操作一：第 i 天没有操作，沿用前一天卖出股票的状态，即：dp[i] [2] = dp[i - 1] [2]
    • 操作二：第 i 天卖出股票了，那么dp[i] [2] = dp[i - 1] [1] + prices[i]
  • dp[i] [3] = max(dp[i - 1] [3], dp[i - 1] [2] - prices[i])
    • 操作一：第 i 天没有操作，沿用前一天买入股票的状态，即：dp[i] [3] = dp[i - 1] [3]
    • 操作二：第 i 天卖出股票了，那么dp[i] [3] = dp[i - 1] [2] - prices[i]
  • dp[i] [4] = max(dp[i - 1] [4], dp[i - 1] [3] + prices[i])
    • 操作一：第 i 天没有操作，沿用前一天卖出股票的状态，即：dp[i] [4] = dp[i - 1] [4]
    • 操作二：第 i 天卖出股票了，那么dp[i] [4] = dp[i - 1] [3] + prices[i]

• 3、dp 数组初始化

  • dp[i] [0] = dp[i - 1] [0]
    • 第0天没有操作，这个最容易想到，就是0
  • dp[i] [1] = -prices[0]
    • 不用管第几次，现在手头上没有现金，只要买入，现金就做相应的减少。
  • dp[i] [2] = 0
    • 从递推公式中可以看出每次是取最大值，那么既然是收获利润如果比0还小了就没有必要收获这个利润了。
  • dp[i] [3] = -prices[0]
    • 不用管第几次，现在手头上没有现金，只要买入，现金就做相应的减少。
  • dp[i] [4] = 0
    • 从递推公式中可以看出每次是取最大值，那么既然是收获利润如果比0还小了就没有必要收获这个利润了。

• 4、确定遍历顺序

  • 一定是从前向后啦~~

​ 在上面分析的基础上进行空间的优化，因为 dp数组可以沿用前一个状态

第309题 有一天冷冻期的股票交易

• 时间复杂度：O(n)
• 空间复杂度：O(n)

动态规划五部曲：

• 1、确定 dp 数组以及下标的含义

  • dp[i] [j]，第i天状态为j，所剩的最多现金为dp[i] [j]。
    • j = 0 ：持有股票状态 ：分为今天买入，和之前买入
    • j = 1 ：不持有股票状态1：分为两天前已经将股票卖出，处于可以操作股票状态
    • j = 2 ：不持有股票状态2：今天卖出，处于不能操作股票状态
    • j = 3 ：不持有股票状态3：冷冻期状态，注意这个状态仅保持一天，也就是前一天卖出股票，处于不能操作股票状态
  • 如果把状态2和状态4合并为一个状态，分成三个状态来进行分析的话，那就会比较模糊了，从代码上讲可以合并，但是比较难理解。

• 2、确定递推公式

  • 对于 dp[i] [0] = max(dp[i - 1] [0], max(dp[i - 1] [3], dp[i - 1] [1]) - prices[i]）
    • 操作一：dp[i] [0] = dp[i - 1] [0]，前一天已经是持有股票状态，今天保持就好
    • 操作二：前一天是 j = 1 状态，且今天买入
    • 操作三：前一天是 j = 3 状态，且今天买入
    • 因此对于买入状态，需要先求出 dp[i - 1] [3] 和 dp[i - 1] [1] 的最大值，在减去 prices[i] ，最终与操作一相比取最大值
  • 对于 dp[i] [1] = max(dp[i - 1] [1], dp[i - 1] [3]);
    • 操作一：前一天是 j = 2 状态
    • 操作二：前一天是 j = 4 状态
  • 对于 dp[i] [2] = dp[i - 1] [0] + prices[i]
    • 此时只有这一种操作。
  • 对于 dp[i] [3] = dp[i - 1] [2]
    • 此时也只有这一种操作

• 3、dp 数组如何初始化

  • dp[0] [0] = -prices[0]，其余三个状态下对应的为 0

• 4、确定遍历顺序

  • 一定是从前往后啦~~

5、最长上升子序列

第300题 最长递增子序列

最长上升子序列是动规的经典题目之一，因为这里的 dp[i] 可以根据 dp[j] ( j < i )，推导出来。

动态规划五部曲

• 1、确定 dp 数组以及下标的含义

  • dp[i] 表示 包括 i 以及它前面的最长上升子序列

• 2、状态转移方程

  • 位置 i 的最长升序子序列等于 j 从 0 到 i-1 各个位置的最长上升子序列 +1 的最大值
  • 所以 if ( nums[i] > nums[j] ) { dp[i] = max(dp[i], dp[j] + 1); }
  • 注意这里不是要 dp[i] 与 dp[j] + 1 进行比较，而是我们要取dp[j] + 1的最大值

• 3、dp[i] 的初始化

  • 每一个i ，对应的上升序列的长度至少为 1。

• 4、确定遍历顺序

  • 一定是从前向后的啦~
  • j 其实就是 0 - ( i- 1 ) 区间，遍历i 在外层，遍历 j 在内层。

第674题 最长连续递增子序列

动规五部曲分析如下：

• 1、确定dp数组（dp table）以及下标的含义

  • dp[i]：以下标i为结尾的数组的连续递增的子序列长度为dp[i]。
  • 注意这里的定义，一定是以下标i为结尾，并不是说一定以下标0为起始位置。

• 2、确定递推公式

  • if ( nums[i + 1] > nums[i] ) dp[i + 1] = dp[i] + 1;
  • 满足判断条件，则以 i+1 为结尾的数组的连续递增的子序列长度 一定等于 以i为结尾的数组的连续递增的子序列长度 + 1 。
  • 因为本题要求连续递增子序列，所以就必要比较nums[i + 1]与nums[i]，而不用去比较nums[j]与nums[i] （j是在0到i之间遍历）。既然不用j了，那么也不用两层for循环，本题一层for循环就行，比较nums[i + 1] 和 nums[i]。

• 3、dp数组初始化

  • 以下标i为结尾的数组的连续递增的子序列长度最少也应该是1，即就是nums[i]这一个元素。
  • 所以dp[i]应该初始1;

• 4、确定遍历顺序

  • 从递推公式上可以看出， dp[i + 1]依赖dp[i]，所以一定是从前向后遍历。

总结

​ 子序列 VS 子数组（连续子序列） 的处理不一样，好好细品上面几道题哦 ~

6、编辑距离

第392题 判断子序列

这道题目 其实是可以用双指针或者贪心的的

​ 这道题目算是编辑距离的入门题目（毕竟这里只是涉及到减法），也是动态规划解决的经典题型。

​ 这一类题都是题目读上去感觉很复杂，模拟一下也发现很复杂，用动规分析完了也感觉很复杂，但是最终代码却很简短。

​ 编辑距离的题目最能体现出动规精髓和巧妙之处

动态规划五部曲

• 1、确定dp数组以及下标的含义

  • dp[i] [j] 表示以下标 i-1 为结尾的字符串s，和以下标j-1为结尾的字符串t，相同子序列的长度为dp[i] [j]。
  • 本题是判断 s 是否为 t 的子序列，也就是判断，t 的长度时否 大于等于 s。
  • 也就是 行 是较小的字符串，列 是较大的字符串。
  • 在第 3 步中解释了为什么要定义为 i-1 和 j-1 ，而不是 i 和 j 。

• 2、确定递推公式

  • 操作一：if (s[i - 1] == t[j - 1])
    • t 中找到了一个字符在s中也出现了
    • 那么dp[i] [j] = dp[i - 1] [j - 1] + 1
  • 操作二：if (s[i - 1] != t[j - 1])
    • 相当于 t 要删除元素，继续匹配，t 如果把当前元素t[j - 1]删除，那么dp[i] [j] 的数值就是 看s[i - 1]与 t[j - 2]的比较结果了
    • 也就是等于左边的值。 dp[i] [j] = dp[i] [j - 1]

• 3、dp 数组初始化

  • 由递推公式看，dp[i] [0] 和 dp[0] [j] 都是需要初始化的
  • 从递推公式可以解释，为什么要把 dp 数组定义为 i-1 结尾 和 j-1 结尾的字符串，
  • 因为这样的定义在 dp 二维矩阵中可以留出初始化的空间
  • 如果要是定义的dp[i] [j]是以下标i为结尾的字符串s和以下标j为结尾的字符串t，初始化就比较麻烦了。

• 4、确定遍历顺序

  • dp[i] [j] 都是依赖于前一个的状态，因此遍历顺序一定是从上到下，从左往右。

第115题 不同的子序列

这道题如果是求连续的子序列，那么就可以考虑 KMP 算法，这道题目双指针法可就做不了，然而本题是求 子序列。

动态规划五部曲：

• 1、确定 dp 数组以及下标的含义

  • dp[i] [j]： 以 i-1 结尾的 s 字符串的子序列 出现在 以 j-1 结尾的 t 字符串中的个数为 dp[i] [j]
  • 也就是 行 是较小的字符串，列 是较大的字符串。

• 2、确定递推公式

  • 情况一：s[i - 1] 与 t[j - 1]相等，dp[i] j] = dp[i - 1] [j - 1] + dp[i - 1] [j]。
    • 此时 dp[i] [j] 由两部分组成
    • 操作一：用 s[i - 1] 来匹配，那么个数为 dp[i - 1] [j - 1]
    • 操作二：不用s[i - 1]来匹配，那么个数为dp[i - 1] [j]。
    • 举个例子：s：bagg 和 t：bag 。
      • 用 s[3] 来匹配，s[0] s[1] s[3]组成的 bag。
      • 不用 s[3] 来匹配，s[0] s[1] s[2]组成的 bag。
  • 情况二：s[i - 1] 与 t[j - 1]不相等，dp[i] [j] = dp[i - 1] [j]
    • 此时只有一种操作，那就是不用 s[i - 1]

• 3、dp 数组初始化

  • 从递推公式看出，dp[i] [0] 和 dp[0] [j] 是一定要初始化的，初始化的时候不要凭空来想象，回想一下 dp 数组的定义。
    • dp[i] [0] ：以i-1为结尾的s可以随便删除元素，出现空字符串的个数，所以把以i-1为结尾的s，删除所有元素，出现空字符串的个 数就是1。所以 dp[i] [0] = 1;
    • dp[0] [j]：空字符串 s 可以随便删除元素，出现以 j-1 为结尾的字符串t的个数。此时dp[0] [j]一定都是0，s如论如何也变成不了t 。 所以 dp[0] [j] = 0。
    • dp[0] [0]：这个位置表示 空字符串 s 可以删除 0 个元素，变成空字符串 t。所以 dp[0] [0] = 0。

• 4、确定遍历顺序

  • 由递推公式可以看出，dp[i] [j] 都是根据左上方 和 正上方推出来的。所以遍历的顺序一定是从上到下，从左到右。

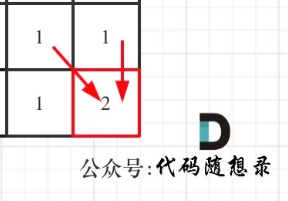
第583题 两个字符串的删除

本题与 第115题 不同的就是，两个字符串都可以做删除操作，情况虽然复杂了，但是整体的思路是不变的。本题是两个字符串可以互相删。

动态规划五部曲：

• 1、确定 dp 数组以及下标含义

  • 题意是：找到使word1和word2相同所需的最下步数，每一步可以删除任意一个字符串中的一个字符。
  • dp[i] [j] ：以 i-1 结尾的 word1，和以 j-1 结尾的 word2，达到相同所走的最小步数，也就是删除元素的最少次数。

• 2、确定递推公式

  • 情况一：word1[i - 1] = word2[j - 1]
    • dp[i] [j] = dp[i - 1] [j - 1] 这个时候不需要删除嘛
  • 情况二：word1[i - 1] != word2[j - 1]
    • 操作一：删除word1[i - 1]，则 dp[i] [j] = dp[i - 1] [j] + 1
    • 操作二：删除word2[i - 1]，则 dp[i] [j] = dp[i] [j - 1] + 1
    • 操作三：删除word1[i - 1]同时删除word2[i - 1]，则 dp[i] [j] = dp[i - 1] [j] + 2
    • 所以要取三者的最小值。 dp[i] [j] = min({dp[i - 1] [j - 1] + 2, dp[i - 1] [j] + 1, dp[i] [j - 1] + 1}) 注意三个元素取最小值，则用大括号

• 3、dp 数组初始化

  • 从递推公式可以看出，dp[i] [0] 和 dp[0] [j] 是一定需要初始化的。
  • dp[i] [0]：word2为空字符串，以 i-1 为结尾的字符串word2要删除多少个元素，才能和word1相同呢，很明显 dp[i] [0] = i。
  • dp[0] [j]：word1为空字符串，以 j-1 为结尾的字符串word1要删除多少个元素，才能和word2相同呢，很明显 dp[0] [j] = j。

• 4、确定遍历顺序

  • 从递推公式可以看出，dp[i] [j] 是根据 左上方、正上方、正左方 推导出的，
  • 所以遍历顺序是 从上到下，从左到右。

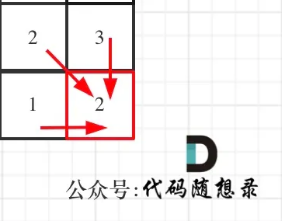
第72题 编辑距离

编辑距离是用动规解决的经典题目，这题目看起来好像很复杂，但是实际上用动规可以很巧妙的算出最少的编辑距离。

动态规划五部曲

• 1、确定 dp 数组以及下标含义

  • dp[i] [j] 表示以下标 i-1 为结尾的字符串 word1 和 以下标 j-1 为结尾的字符串 word2，最少的编辑距离为 dp[i] [j]
  • 这部分题中有好多次出现表示的都是 i-1 和 j-1 ，这样为了将初始化和后面的递推相统一，简化操作。

• 2、确定递推公式

  • 在确定递推公式的时候，首先需要考虑清楚 以下 4 种情况。
  • 情况一：word1[i - 1] == word2[j - 1]
    • 不做任何操作，dp[i] [j] = dp[i - 1] [j - 1]
    • word1[i - 1] 与 word2[j - 1]相等了，那么就不用编辑了，
    • 就可以直接以下标 i-2 为结尾的字符串word1和以下标 j-2 为结尾的字符串word2的最近编辑距离dp[i - 1] [j - 1] 就是 dp[i] [j]了。
  • 情况二：word1[i - 1] != word2[j - 1]
    • 操作一：增
      • word1 增加一个元素，使 word1[i - 1] == word2[j - 1]，那么就是以下标为 i-2 为结尾的 word1 与 下标为 j-1 为结尾的 word2的最近编辑距离 加上1，表示为： dp[i] [j] = dp[i - 1] [j] + 1
    • 操作二：删
      • 这里要想明白一个点：word2添加一个元素，相当于word1删除一个元素
      • 对 word1 的删除操作，就相当于对 word2 添加元素，所以这种操作就可以表示为dp[i] [j] = dp[i] [j - 1] + 1
    • 操作三：换
      • word1 替换为 word[i - 1]，使其与 word2 [j - 1] 相同
      • 刚刚愣了一下神，在想为啥是 i -1 和 j -1，傻了吧，本来 dp 数组的定义就是这样呀，你在看看 dp 数组的定义嘛
      • 所以此时 dp[i] [j] = dp[i - 1] [j - 1] + 1
    • 综上，第二种情况下，要取三种操作的最小值。
      • dp[i] [j] = min({dp[i - 1] [j - 1], dp[i - 1] [j], dp[i] [j - 1]}) + 1;

• 3、dp 数组初始化

  • dp[i] [0] ：以下标 i-1 为结尾的字符串word1，和 空字符串word2，最近编辑距离为dp[i] [0]， dp[i] [0] = i
  • dp[0] [j] ：以下标 j-1 为结尾的字符串word2，和 空字符串word1，最近编辑距离为dp[0] [j]， dp[0] [j] = j

• 4、确定遍历顺序

  • 从递推公式可以看出，dp[i] [j] 是根据 左上方、正上方、正左方 推导出的，
  • 所以遍历顺序是 从上到下，从左到右。

总结 绝杀编辑距离的三个铺垫

真的很哇塞！

7、回文串

question 1、回文串定义：

​ 正着读和反着读都一样的字符串。

question 2、回文子串 VS 回文子序列

回文子串是要连续的，回文子序列可不是连续的

回文子串，回文子序列都是动态规划经典题目。

第647题 回文子串

解题方法：

• 解法一：暴力解法
  • 时间复杂度：O(n^3)
• 解法二：动态规划
  • 时间复杂度：O(n^2）
  • 空间复杂度：O(n^2)
• 解法三：双指针法
  • 时间复杂度：O(n^2)
  • 空间复杂度：O(1)

解法二：

动态规划五部曲：

• 1、确定 dp 数组以及下标的含义

  • 本题比较特殊哦，使用了 布尔类型的 dp 数组
  • dp[i] [j] ：表示区间范围是 [i, j] （注意是左闭右闭区间）的子串是否是回文子串，
  • 如果是 dp[i] [j] = true， 如果不是 dp[i] [j] =false

• 2、确定递推公式

  • 情况一：s[i] = s[j]
    • 操作一：下标 i 与下标 j 相同，也就是说区间内只有一个字符，那当然是回文串，此时 dp[i] [j] = true
    • 操作二：下标 i 与下标 j 相差为 1，这也是回文串呀，此时 dp[i] [j] = true
    • 操作三：下标 i 与下标 j 相差大于 1，例如cabac，此时s[i]与s[j]已经相同了，我们看i到j区间是不是回文子串就看aba是不是回文就可以了，那么aba的区间就是 i+1 与 j-1区间，这个区间是不是回文就看dp[i + 1] [j - 1]是否为true。
  • 情况二：s[i] != s[j]
    • 此时 dp[i] [j] = false

• 3、dp 数组初始化

  • dp[i] [j] 肯定不是全部初始化为 true ，所以将其初始化为 false

• 4、确定遍历顺序

  • 这题的遍历顺序就有讲究了
  • 从递推公式可以看出，操作三 是根据 dp[i + 1] [j - 1]是否为 true 来对 dp[i] [j] 进行赋值的
  • dp[i + 1] [j - 1] 在 dp[i] [j]的左下角，所以一定要从下到上，从左到右遍历，这样保证dp[i + 1] [j - 1]都是经过计算的。

解法三：双指针法

先找中心，以中心向两边扩散，看看是不是对称，由此来判断是否是回文串。

在遍历中心点的时候，要注意中心点有两种情况。

• 一个元素可以作为中心，（三个元素作为中心跟一个元素作为中心是类似的，相当于在一个元素的左右各添加一个元素得到。）
• 两个元素也可以作为中心，（同理四个元素作为中心和两个元素作为中心也是等价的。）

第516题 最长回文子序列

本题是求回文子序列，也就是不要求连续咯~

本题可以用马拉车算法

动态规划五部曲：

• 1、确定 dp 数组以及下标的含义
  • dp[i] [j] ： 字符串 s 在 [i, j] 范围内最长的回文子序列的长度 dp[i] [j]
• 2、确定递推公式
  • 情况一：s[i] = s[j]
    • dp[i] [j] = dp[i + 1] [j - 1] + 2
  • 情况二：s[i] ！= s[j]
    • 说明s[i]和s[j]的同时加入 并不能增加[i,j]区间回文子串的长度，那么分别加入s[i]、s[j]看看哪一个可以组成最长的回文子序列。
    • 加入s[j]的回文子序列长度为dp[i + 1] [j]。
    • 加入s[i]的回文子序列长度为dp[i] [j - 1]。
    • 所以此时： dp[i] j] = max(dp[i + 1] [j], dp[i] [j - 1]);

• 3、dp 数组初始化

  • 首先要考虑当 i 和 j 相同的情况，从递推公式可以看出，是计算不到 i=j 的情况的，所以需要手动初始化一下，
  • i=j ，则 dp[i] [j] = 1，也就是一个字符的回文子序列的长度就是 1。
  • 其他情况的 dp[i] [j] 初始化为 0 即可。
  • 这样情况二中的递推公式 dp[i] [j] 才不会被初始值覆盖。

• 4、确定遍历顺序

  • 从递推公式可以看出，dp[i] [j] 依赖于 dp[i + 1] [j - 1] 和 dp[i + 1] [j]
  • 所以遍历顺序一定是从下到上，从左到右，才能保证CIA一行的数据是经过计算的

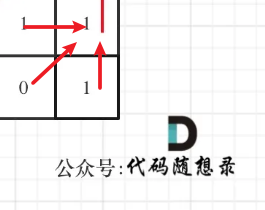
8、总结：

8.1 编辑距离

• 这几道题给定的是两个字符串，
• 要区分是等价为求 子序列（不连续） 还是 子数组（连续）
• 还有个比较新颖的点是 dp 数组中 用 dp[i] [j] 来表征 i-1 、j-1 相关的信息

8.2 回文串

• 区分是求 **回文子序列（不连续）**还是 回文子串（连续）
• 这个类型题中的 dp 数组，需要把一个字符串从两个维度来分析，展成一个二维的，有点不太习惯，需要画图做题适应一下。
• 这个二维图推断的时候，都是左下角的部分不参与，最后只有右上角参与了判断。
• 这个题型的 dp 数组，是把两个维度当做一个闭区间进行判断，因为是闭区间，所以天生就有 i <= j
  • 判断回文子串时，设为 bool 类型，判断区间内是否是回文子串
  • 判断回文子序列时，设为 int 类型，用来存储区间内的最长回文子序列，这里的初始化也很特别，i=j 时初始化为 1， 其余为0，
• dp 数组的遍历顺序也很巧妙
  • 回文子串时，i 是从 s.size()-1 到 0，j 是从 i 到 s.size()-1
  • 回文子序列时，i 是从 s.size()-1 到 0，j 是从 i+1 到 s.size()-1，这里为啥是 i+1 呢，因为 i=j 已经初始化时赋值了，我们就是要根据这个初始化来进行接下来的所有推理呀