LCS/LIS/LCIS

LCS

这里仅仅记录一下LCS算法的思路：典型的DP,空间换时间

step 1: 先比较两个子串的对应位是否相同，如果相同，则b[i][j]='\',并且c[i][j]=c[i-1][j-1]+1，否则转向step2

step 2:如果上角的值>=左角的值，那么将上角的值赋给c[i][j]，同时b[i][j]箭头指向大值(指向上角)。如果上角的值<左角的值，箭头指向大值(指向左)，左角的值赋给c[i][j]

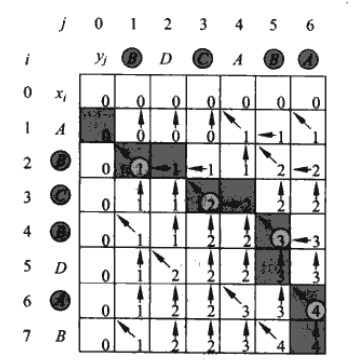
实例：

求X=<A,B,C,B,D,A,B>和Y=<B,D,C,A,B,A>的最长公共子序列，在第一行中，第一行为A和第4列第6列的值A相同，

于是b[][]中存储的箭头指向上对角。同时c[][]的值为上对角的值+1。如果X,Y对应的相应位不同，那么b[][]的箭头总是

指向大值，如果两值相等，则指向上面那一个。遍历完之后，就可以得出b[][]和c[][],就能确定LCS。

要点：

1.b[i][j]存放的是箭头，若Xi=＝Yi，则箭头指向对角线b[i-1][j-1]，否则箭头总是指向大值，

若上值b[i-1][j]和左值b[i][j-1]相等，优先指向上值。
2.c[i][j]存放的是数值，若Xi==Yi,则c[i][j]值为上对角值c[i-1][j-1]+1,否则c[i][j]＝max(c[i][j-1],c[i-1][j])

代码:

#include<iostream>
using namespace std;
#define M 7
#define N 6
int b[M+1][N+1]={0};//保存箭头
int c[M+1][N+1]={0};//保存值

void Lcs_Length(char* X,char* Y)
{
	int i,j;
	for(i=1;i<=M;i++)//第0列置0
		c[i][0]=0;
	for(j=0;j<=N;j++)
		c[0][j]=0;  //第0行置0
	for(i=1;i<=M;i++)
	{
		for(j=1;j<=N;j++)
		{
			if(X[i]==Y[j])//比较两个字串对应位，如果相等，则=对角+1
			{
				c[i][j]=c[i-1][j-1]+1;
				b[i][j]=1;//1代表↖　
			}
			else if(c[i-1][j]>=c[i][j-1])//如果上面值>=下面值
			{
				c[i][j]=c[i-1][j];//c[i][j]=大值
				b[i][j]=2;//2代表↑
			}
			else 
			{
				c[i][j]=c[i][j-1];//赋的总是大值，箭头总是指向大值
				b[i][j]=3;//3代表←
			}
		}
	}
}
void Print_Lcs(char* X,int i,int j)
{
	if(i==0 || j==0)
		return ;
	if(b[i][j]==1)
	{
		Print_Lcs(X,i-1,j-1);
		cout<<X[i]<<' ';//只需输出↖对应的值
	}
	else if(b[i][j]==2)
		Print_Lcs(X,i-1,j);
	else Print_Lcs(X,i,j-1);
}
void main()
{
	 char  X[M+1] = {'0','A','B','C','B','D','A','B'};  
	 char  Y[N+1] = {'0','B','D','C','A','B','A'};  
    Lcs_Length(X, Y);  
    Print_Lcs(X, M, N);  
	cout<<endl;
	for(int i=0;i<=M;i++)
	{
		for(int j=0;j<=N;j++)
		{
			cout<<c[i][j]<<' ';
		}
		cout<<endl;
	}
	cout<<endl;
	for(int i=0;i<=M;i++)
	{
		for(int j=0;j<=N;j++)
		{
			switch(b[i][j])
			{
			case 0:
				{
					cout<<b[i][j]<<"  ";
					break;
				}
			case 1:
				{
					cout<<"↖"<<' ';
					break;
				}
			case 2:
				{
					cout<<"↑"<<' ';
					break;
				}
			case 3:
				{
					cout<<"←"<<' ';
					break;
				}
			}
		}
		cout<<endl;
	}
}

LCIS

以下来自百度文库：

最长公共上升子序列（LCIS）的O(n^2)算法

预备知识：动态规划的基本思想，LCS，LIS。

问题：字符串a，字符串b，求a和b的LCIS（最长公共上升子序列）。

首先我们可以看到，这个问题具有相当多的重叠子问题。于是我们想到用DP搞。DP的首要任务是什么？定义状态。

1定义状态F[i][j]表示以a串的前i个字符b串的前j个字符且以b[j]为结尾构成的LCIS的长度。

为什么是这个而不是其他的状态定义？最重要的原因是我只会这个，还有一个原因是我知道这个定义能搞到平方的算

法。而我这只会这个的原因是，这个状态定义实在是太好用了。这一点我后面再说。