hashtable

Hash

From Wikipedia, the free encyclopedia

Jump to: navigation, search

Look up hash in Wiktionary, the free dictionary.

Hash may refer to:

Substances

• Hash (food), a coarse mixture of ingredients
• Hashish, a cannabis product

Organizations

• Hash House Harriers, a running club

Hash mark

• Hash marks, a marking on hockey rinks and gridiron football fields
• Hatch mark, a form of mathematical notation
• Service stripe, a military decoration
• Tally mark, a counting notation

In linguistics

• Hash symbol or hash mark, the glyph #

In computing

• Hash function, a derivation of data, notably seen in cryptographic hash functions
• Hashtag, a form of metadata often used on social networking websites
• Cryptographic hash function, a derivation of data used to authenticate message integrity
• Hash table, a data structure
• hash (Unix), an operating system command
• Fragment identifier, in computer hypertext, a string of characters that refers to a subordinate resource
• Geohash, a spatial data structure which subdivides space into buckets of grid shape
• Hash chain, a method of producing many one-time keys from a single key or password

Hash function

From Wikipedia, the free encyclopedia

Jump to: navigation, search

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. (July 2010)

A hash function that maps names to integers from 0 to 15. There is a collision between keys "John Smith" and "Sandra Dee".

A hash function is any algorithm that maps data of variable length to data of a fixed length. The values returned by a hash function are called hash values, hash codes, hash sums, checksums or simply hashes.

Description

This section may require copy editing for veering off-topic and not giving a comprehensive description of the properties of hash functions. You can assist by editing it. (May 2013)

Hash functions are primarily used to generate fixed-length output data that acts as a shortened reference to the original data. This is useful when the output data is too cumbersome to use in its entirety.

One practical use is a data structure called a hash table where the data is stored associatively. Searching for a person's name in a list is slow, but the hashed value can be used to store a reference to the original data and retrieve constant time (barring collisions). Another use is in cryptography, the science of encoding and safeguarding data. It is easy to generate hash values from input data and easy to verify that the data matches the hash, but hard to 'fake' a hash value to hide malicious data. This is the principle behind the Pretty Good Privacy algorithm for data validation.

Hash functions are also used to accelerate table lookup or data comparison tasks such as finding items in a database, detecting duplicated or similar records in a large file, finding similar stretches in DNA sequences, and so on.

A hash function should be referentially transparent (stable), i.e., if called twice on input that is "equal" (for example, strings that consist of the same sequence of characters), it should give the same result. There is a construct in many programming languages that allows the user to override equality and hash functions for an object: if two objects are equal, their hash codes must be the same. This is crucial to finding an element in a hash table quickly, because two of the same element would both hash to the same slot.

Hash functions are destructive, akin to lossy compression, as the original data is lost when hashed. Unlike compression algorithms, where something resembling the original data can be decompressed from compressed data, the goal of a hash value is to uniquely identify a reference to the object so that it can be retrieved in its entirety. Unfortunately, all hash functions that map a larger set of data to a smaller set of data cause collisions. Such hash functions try to map the keys to the hash values as evenly as possible because collisions become more frequent as hash tables fill up. Thus, single-digit hash values are frequently restricted to 80% of the size of the table. Depending on the algorithm used, other properties may be required as well, such as double hashing and linear probing. Although the idea was conceived in the 1950s, the design of good hash functions is still a topic of active research.^[1]

Hash functions are related to (and often confused with) checksums, check digits, fingerprints, randomization functions, error correcting codes, and cryptographic hash functions. Although these concepts overlap to some extent, each has its own uses and requirements and is designed and optimized differently. The HashKeeper database maintained by the American National Drug Intelligence Center, for instance, is more aptly described as a catalog of file fingerprints than of hash values.

Hash tables

Hash functions are primarily used in hash tables, to quickly locate a data record (e.g., a dictionary definition) given its search key (the headword). Specifically, the hash function is used to map the search key to an index; the index gives the place in the hash table where the corresponding record should be stored. Hash tables, in turn, are used to implement associative arrays and dynamic sets.

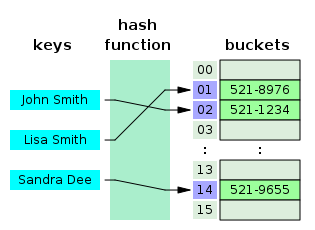
Typically, the domain of a hash function (the set of possible keys) is larger than its range (the number of different table indexes), and so it will map several different keys to the same index. Therefore, each slot of a hash table is associated with (implicitly or explicitly) a set of records, rather than a single record. For this reason, each slot of a hash table is often called a bucket, and hash values are also called bucket indices.

Thus, the hash function only hints at the record's location—it tells where one should start looking for it. Still, in a half-full table, a good hash function will typically narrow the search down to only one or two entries.

Caches

Hash functions are also used to build caches for large data sets stored in slow media. A cache is generally simpler than a hashed search table, since any collision can be resolved by discarding or writing back the older of the two colliding items. This is also used in file comparison.

Bloom filters

Main article: Bloom filter

Hash functions are an essential ingredient of the Bloom filter, a space-efficient probabilistic data structure that is used to test whether an element is a member of a set.

Finding duplicate records

Main article: Hash table

When storing records in a large unsorted file, one may use a hash function to map each record to an index into a table T, and collect in each bucket T[i] a list of the numbers of all records with the same hash value i. Once the table is complete, any two duplicate records will end up in the same bucket. The duplicates can then be found by scanning every bucket T[i] which contains two or more members, fetching those records, and comparing them. With a table of appropriate size, this method is likely to be much faster than any alternative approach (such as sorting the file and comparing all consecutive pairs).

Finding similar records

Main article: Locality sensitive hashing

Hash functions can also be used to locate table records whose key is similar, but not identical, to a given key; or pairs of records in a large file which have similar keys. For that purpose, one needs a hash function that maps similar keys to hash values that differ by at most m, where m is a small integer (say, 1 or 2). If one builds a table T of all record numbers, using such a hash function, then similar records will end up in the same bucket, or in nearby buckets. Then one need only check the records in each bucket T[i] against those in buckets T[i+k] where k ranges between −m and m.

This class includes the so-called acoustic fingerprint algorithms, that are used to locate similar-sounding entries in large collection of audio files. For this application, the hash function must be as insensitive as possible to data capture or transmission errors, and to "trivial" changes such as timing and volume changes, compression, etc.^[2]

Finding similar substrings

The same techniques can be used to find equal or similar stretches in a large collection of str

Geometric hashing

This principle is widely used in computer graphics, computational geometry and many other disciplines, to solve many proximity problems in the plane or in three-dimensional space, such as finding closest pairs in a set of points, similar shapes in a list of shapes, similar images in an image database, and so on. In these applications, the set of all inputs is some sort of metric space, and the hashing function can be interpreted as a partition of that space into a grid of cells. The table is often an array with two or more indices (called a grid file, grid index, bucket grid, and similar names), and the hash function returns an index tuple. This special case of hashing is known as geometric hashing or the grid method. Geometric hashing is also used in telecommunications (usually under the name vector quantization) to encode and compress multi-dimensional signals.

Properties

Good hash functions, in the original sense of the term, are usually required to satisfy certain properties listed below. Note that different requirements apply to the other related concepts (cryptographic hash functions, checksums, etc.).

Determinism

A hash procedure must be deterministic—meaning that for a given input value it must always generate the same hash value. In other words, it must be a function of the data to be hashed, in the mathematical sense of the term. This requirement excludes hash functions that depend on external variable parameters, such as pseudo-random number generators or the time of day. It also excludes functions that depend on the memory address of the object being hashed, because that address may change during execution (as may happen on systems that use certain methods of garbage collection), although sometimes rehashing of the item is possible.

Uniformity

A good hash function should map the expected inputs as evenly as possible over its output range. That is, every hash value in the output range should be generated with roughly the same probability. The reason for this last requirement is that the cost of hashing-based methods goes up sharply as the number of collisions—pairs of inputs that are mapped to the same hash value—increases. Basically, if some hash values are more likely to occur than others, a larger fraction of the lookup operations will have to search through a larger set of colliding table entries.

Note that this criterion only requires the value to be uniformly distributed, not random in any sense. A good randomizing function is (barring computational efficiency concerns) generally a good choice as a hash function, but the converse need not be true.

Hash tables often contain only a small subset of the valid inputs. For instance, a club membership list may contain only a hundred or so member names, out of the very large set of all possible names. In these cases, the uniformity criterion should hold for almost all typical subsets of entries that may be found in the table, not just for the global set of all possible entries.

In other words, if a typical set of m records is hashed to n table slots, the probability of a bucket receiving many more than m/n records should be vanishingly small. In particular, if m is less than n, very few buckets should have more than one or two records. (In an ideal "perfect hash function", no bucket should have more than one record; but a small number of collisions is virtually inevitable, even if n is much larger than m – see the birthday paradox).

When testing a hash function, the uniformity of the distribution of hash values can be evaluated by the chi-squared test.

Variable range

In many applications, the range of hash values may be different for each run of the program, or may change along the same run (for instance, when a hash table needs to be expanded). In those situations, one needs a hash function which takes two parameters—the input data z, and the number n of allowed hash values.

A common solution is to compute a fixed hash function with a very large range (say, 0 to 2³² − 1), divide the result by n, and use the division's remainder. If n is itself a power of 2, this can be done by bit masking and bit shifting. When this approach is used, the hash function must be chosen so that the result has fairly uniform distribution between 0 and n − 1, for any value of n that may occur in the application. Depending on the function, the remainder may be uniform only for certain values of n, e.g. odd or prime numbers.

We can allow the table size n to not be a power of 2 and still not have to perform any remainder or division operation, as these computations are sometimes costly. For example, let n be significantly less than 2^b. Consider a pseudo random number generator (PRNG) function P(key) that is uniform on the interval [0, 2^b − 1]. A hash function uniform on the interval [0, n-1] is n P(key)/2^b. We can replace the division by a (possibly faster) right bit shift: nP(key) >> b.

Variable range with minimal movement (dynamic hash function)

When the hash function is used to store values in a hash table that outlives the run of the program, and the hash table needs to be expanded or shrunk, the hash table is referred to as a dynamic hash table.

A hash function that will relocate the minimum number of records when the table is resized is desirable. What is needed is a hash function H(z,n) – where z is the key being hashed and n is the number of allowed hash values – such that H(z,n + 1) = H(z,n) with probability close to n/(n + 1).

Linear hashing and spiral storage are examples of dynamic hash functions that execute in constant time but relax the property of uniformity to achieve the minimal movement property.

Extendible hashing uses a dynamic hash function that requires space proportional to n to compute the hash function, and it becomes a function of the previous keys that have been inserted.

Several algorithms that preserve the uniformity property but require time proportional to n to compute the value of H(z,n) have been invented.

Data normalization

In some applications, the input data may contain features that are irrelevant for comparison purposes. For example, when looking up a personal name, it may be desirable to ignore the distinction between upper and lower case letters. For such data, one must use a hash function that is compatible with the data equivalence criterion being used: that is, any two inputs that are considered equivalent must yield the same hash value. This can be accomplished by normalizing the input before hashing it, as by upper-casing all letters.

Continuity

A hash function that is used to search for similar (as opposed to equivalent) data must be as continuous as possible; two inputs that differ by a little should be mapped to equal or nearly equal hash values.^{[citation needed]}

Note that continuity is usually considered a fatal flaw for checksums, cryptographic hash functions, and other related concepts. Continuity is desirable for hash functions only in some applications, such as hash tables used in Nearest neighbor search.

Hash function algorithms

For most types of hashing functions the choice of the function depends strongly on the nature of the input data, and their probability distribution in the intended application.

Trivial hash function

If the datum to be hashed is small enough, one can use the datum itself (reinterpreted as an integer in binary notation) as the hashed value. The cost of computing this "trivial" (identity) hash function is effectively zero. This hash function is perfect, as it maps each input to a distinct hash value.

The meaning of "small enough" depends on the size of the type that is used as the hashed value. For example, in Java, the hash code is a 32-bit integer. Thus the 32-bit integer Integer and 32-bit floating-point Float objects can simply use the value directly; whereas the 64-bit integer Long and 64-bit floating-point Double cannot use this method.

Other types of data can also use this perfect hashing scheme. For example, when mapping character strings between upper and lower case, one can use the binary encoding of each character, interpreted as an integer, to index a table that gives the alternative form of that character ("A" for "a", "8" for "8", etc.). If each character is stored in 8 bits (as in ASCII or ISO Latin 1), the table has only 2⁸ = 256 entries; in the case of Unicode characters, the table would have 17×2¹⁶ = 1114112 entries.

The same technique can be used to map two-letter country codes like "us" or "za" to country names (26²=676 table entries), 5-digit zip codes like 13083 to city names (100000 entries), etc. Invalid data values (such as the country code "xx" or the zip code 00000) may be left undefined in the table, or mapped to some appropriate "null" value.

Perfect hashing

Main article: Perfect hash function

A perfect hash function for the four names shown

A hash function that is injective—that is, maps each valid input to a different hash value—is said to be perfect. With such a function one can directly locate the desired entry in a hash table, without any additional searching.

Minimal perfect hashing

A minimal perfect hash function for the four names shown

A perfect hash function for n keys is said to be minimal if its range consists of n consecutive integers, usually from 0 to n−1. Besides providing single-step lookup, a minimal perfect hash function also yields a compact hash table, without any vacant slots. Minimal perfect hash functions are much harder to find than perfect ones with a wider range.

Hashing uniformly distributed data

If the inputs are bounded-length strings (such as telephone numbers, car license plates, invoice numbers, etc.), and each input may independently occur with uniform probability, then a hash function need only map roughly the same number of inputs to each hash value. For instance, suppose that each input is an integer z in the range 0 to N−1, and the output must be an integer h in the range 0 to n−1, where N is much larger than n. Then the hash function could be h = z mod n (the remainder of z divided by n), or h = (z × n) ÷ N (the value z scaled down by n/N and truncated to an integer), or many other formulas.

Warning: h = z mod n was used in many of the original random number generators, but was found to have a number of issues. One of which is that as n approaches N, this function becomes less and less uniform.

Hashing data with other distributions

These simple formulas will not do if the input values are not equally likely, or are not independent. For instance, most patrons of a supermarket will live in the same geographic area, so their telephone numbers are likely to begin with the same 3 to 4 digits. In that case, if m is 10000 or so, the division formula (z × m) ÷ M, which depends mainly on the leading digits, will generate a lot of collisions; whereas the remainder formula z mod m, which is quite sensitive to the trailing digits, may still yield a fairly even distribution.

Hashing variable-length data

When the data values are long (or variable-length) character strings—such as personal names, web page addresses, or mail messages—their distribution is usually very uneven, with complicated dependencies. For example, text in any natural language has highly non-uniform distributions of characters, and character pairs, very characteristic of the language. For such data, it is prudent to use a hash function that depends on all characters of the string—and depends on each character in a different way.

In cryptographic hash functions, a Merkle–Damgård construction is usually used. In general, the scheme for hashing such data is to break the input into a sequence of small units (bits, bytes, words, etc.) and combine all the units b[1], b[2], ..., b[m] sequentially, as follows

S ← S0;                         // Initialize the state.
for k in 1, 2, ..., m do       // Scan the input data units:
  S ← F(S, b[k]);               //   Combine data unit k into the state.
return G(S, n)                 // Extract the hash value from the state.

This schema is also used in many text checksum and fingerprint algorithms. The state variable S may be a 32- or 64-bit unsigned integer; in that case, S0 can be 0, and G(S,n) can be just S mod n. The best choice of F is a complex issue and depends on the nature of the data. If the units b[k] are single bits, then F(S,b) could be, for instance

 if highbit(S) = 0 then
   return 2 * S + b
 else
   return (2 * S + b) ^ P

Here highbit(S) denotes the most significant bit of S; the '*' operator denotes unsigned integer multiplication with lost overflow; '^' is the bitwise exclusive or operation applied to words; and P is a suitable fixed word.^[3]

Special-purpose hash functions

In many cases, one can design a special-purpose (heuristic) hash function that yields many fewer collisions than a good general-purpose hash function. For example, suppose that the input data are file names such as FILE0000.CHK, FILE0001.CHK, FILE0002.CHK, etc., with mostly sequential numbers. For such data, a function that extracts the numeric part k of the file name and returns k mod n would be nearly optimal. Needless to say, a function that is exceptionally good for a specific kind of data may have dismal performance on data with different distribution.

Rolling hash

Main article: rolling hash

In some applications, such as substring search, one must compute a hash function h for every k-character substring of a given n-character string t; where k is a fixed integer, and n is k. The straightforward solution, which is to extract every such substring s of t and compute h(s) separately, requires a number of operations proportional to k·n. However, with the proper choice of h, one can use the technique of rolling hash to compute all those hashes with an effort proportional to k + n.

Universal hashing

A universal hashing scheme is a randomized algorithm that selects a hashing function h among a family of such functions, in such a way that the probability of a collision of any two distinct keys is 1/n, where n is the number of distinct hash values desired—independently of the two keys. Universal hashing ensures (in a probabilistic sense) that the hash function application will behave as well as if it were using a random function, for any distribution of the input data. It will however have more collisions than perfect hashing, and may require more operations than a special-purpose hash function.

Hashing with checksum functions

One can adapt certain checksum or fingerprinting algorithms for use as hash functions. Some of those algorithms will map arbitrary long string data z, with any typical real-world distribution—no matter how non-uniform and dependent—to a 32-bit or 64-bit string, from which one can extract a hash value in 0 through n − 1.

This method may produce a sufficiently uniform distribution of hash values, as long as the hash range size n is small compared to the range of the checksum or fingerprint function. However, some checksums fare poorly in the avalanche test, which may be a concern in some applications. In particular, the popular CRC32 checksum provides only 16 bits (the higher half of the result) that are usable for hashing^{[citation needed]}. Moreover, each bit of the input has a deterministic effect on each bit of the CRC32, that is one can tell without looking at the rest of the input, which bits of the output will flip if the input bit is flipped; so care must be taken to use all 32 bits when computing the hash from the checksum.^[4]

Hashing with cryptographic hash functions

Some cryptographic hash functions, such as SHA-1, have even stronger uniformity guarantees than checksums or fingerprints, and thus can provide very good general-purpose hashing functions.

In ordinary applications, this advantage may be too small to offset their much higher cost.^[5] However, this method can provide uniformly distributed hashes even when the keys are chosen by a malicious agent. This feature may help to protect services against denial of service attacks.

Hashing By Nonlinear Table Lookup

Tables of random numbers (such as 256 random 32 bit integers) can provide high-quality nonlinear functions to be used as hash functions or for other purposes such as cryptography. The key to be hashed would be split into 8-bit (one byte) parts and each part will be used as an index for the nonlinear table. The table values will be added by arithmetic or XOR addition to the hash output value. Because the table is just 1024 bytes in size, it will fit into the cache of modern microprocessors and allow for very fast execution of the hashing algorithm. As the table value is on average much longer than 8 bits, one bit of input will affect nearly all output bits. This is different to multiplicative hash functions where higher-value input bits do not affect lower-value output bits.

This algorithm has proven to be very fast and of high quality for hashing purposes (especially hashing of integer number keys).

Efficient Hashing Of Strings

Modern microprocessors will allow for much faster processing, if 8-bit character Strings are not hashed by processing one character at a time, but by interpreting the string as an array of 32 bit or 64 bit integers and hashing/accumulating these "wide word" integer values by means of arithmetic operations (e.g. multiplication by constant and bit-shifting). The remaining characters of the string which are smaller than the word length of the CPU must be handled differently (e.g. being processed one character at a time).

This approach has proven to speed up hash code generation by a factor of five or more on modern microprocessors of a word size of 64 bit.^{[citation needed]}

Another approach^[6] is to convert strings to a 32 or 64 bit numeric value and then apply a hash function. One method that avoids the problem of strings having great similarity ("Aaaaaaaaaa" and "Aaaaaaaaab") is to use a Cyclic redundancy check (CRC) of the string to compute a 32- or 64-bit value. While it is possible that two different strings will have the same CRC, the likelihood is very small and only requires that one check the actual string found to determine whether one has an exact match. The CRC approach works for strings of any length. CRCs will differ radically^{[dubious – discuss]} for strings such as "Aaaaaaaaaa" and "Aaaaaaaaab".

Locality Sensitive Hashing

Locality-sensitive hashing (LSH) is a method of performing probabilistic dimension reduction of high-dimensional data. The basic idea is to hash the input items so that similar items are mapped to the same buckets with high probability (the number of buckets being much smaller than the universe of possible input items). This is different from the conventional hash functions, such as those used in cryptography, as in this case the goal is to maximize the probability of "collision" of similar items rather than to avoid collisions.^[7]

One example of LSH is MinHash algorithm used for finding similar documents (such as web-pages):

Let h be a hash function that maps the members of A and B to distinct integers, and for any set S define h_min(S) to be the member x of S with the minimum value of h(x). Then h_min(A) = h_min(B) exactly when the minimum hash value of the union A ∪ B lies in the intersection A ∩ B. Therefore,

Pr[h_min(A) = h_min(B)] = J(A,B). where J is Jaccard index.

In other words, if r is a random variable that is one when h_min(A) = h_min(B) and zero otherwise, then r is an unbiased estimator of J(A,B), although it has too high a variance to be useful on its own. The idea of the MinHash scheme is to reduce the variance by averaging together several variables constructed in the same way.

Origins of the term

The term "hash" comes by way of analogy with its non-technical meaning, to "chop and mix". Indeed, typical hash functions, like the mod operation, "chop" the input domain into many sub-domains that get "mixed" into the output range to improve the uniformity of the key distribution.

Donald Knuth notes that Hans Peter Luhn of IBM appears to have been the first to use the concept, in a memo dated January 1953, and that Robert Morris used the term in a survey paper in CACM which elevated the term from technical jargon to formal terminology.^[1]

List of hash functions

Main article: List of hash functions

• NIST hash function competition
• Bernstein hash^[8]
• Fowler-Noll-Vo hash function (32, 64, 128, 256, 512, or 1024 bits)
• Jenkins hash function (32 bits)
• Pearson hashing (8 bits) (64 bit hash C code provided)
• Zobrist hashing

See also

Computer science portal

• Bloom filter
• Coalesced hashing
• Cuckoo hashing
• Hopscotch hashing
• Cryptographic hash function
• Distributed hash table
• Geometric hashing
• Hash table
• HMAC
• Identicon
• Linear hash
• List of hash functions
• Locality sensitive hashing
• MD5
• Perfect hash function
• Rabin–Karp string search algorithm
• Rolling hash
• Transposition table
• Universal hashing
• MinHash
• Low-discrepancy sequence

References

1. ^ ^{a b} Knuth, Donald (1973). The Art of Computer Programming, volume 3, Sorting and Searching. pp. 506–542.
2. ^ "Robust Audio Hashing for Content Identification by Jaap Haitsma, Ton Kalker and Job Oostveen"
3. ^ Broder, A. Z. (1993). "Some applications of Rabin's fingerprinting method". Sequences II: Methods in Communications, Security, and Computer Science. Springer-Verlag. pp. 143–152.
4. ^ Bret Mulvey, Evaluation of CRC32 for Hash Tables, in Hash Functions. Accessed April 10, 2009.
5. ^ Bret Mulvey, Evaluation of SHA-1 for Hash Tables, in Hash Functions. Accessed April 10, 2009.
6. ^ http://citeseer.ist.psu.edu/viewdoc/summary?doi=10.1.1.18.7520 Performance in Practice of String Hashing Functions
7. ^ A. Rajaraman and J. Ullman (2010). "Mining of Massive Datasets, Ch. 3.".
8. ^ "Hash Functions". cse.yorku.ca. September 22, 2003. Retrieved November 1, 2012. "the djb2 algorithm (k=33) was first reported by dan bernstein many years ago in comp.lang.c."

External links

Look up hash in Wiktionary, the free dictionary.

• General purpose hash function algorithms (C/C++/Pascal/Java/Python/Ruby)
• Hash Functions and Block Ciphers by Bob Jenkins
• The Goulburn Hashing Function (PDF) by Mayur Patel
• Hash Function Construction for Textual and Geometrical Data Retrieval Latest Trends on Computers, Vol.2, pp. 483–489, CSCC conference, Corfu, 2010

List of hash functions

From Wikipedia, the free encyclopedia

Jump to: navigation, search

This is a list of hash functions, including cyclic redundancy checks, checksum functions, and cryptographic hash functions.

Cyclic redundancy checks

Main article: Cyclic redundancy check

Name	Length	Type
BSD checksum	16 bits	CRC
checksum	32 bits	CRC
crc16	16 bits	CRC
crc32	32 bits	CRC
crc32 mpeg2	32 bits	CRC
crc64	64 bits	CRC
SYSV checksum	16 bits	CRC

Adler-32 is often classified as a CRC, but it uses a different algorithm.

Checksums

Main article: Checksum

Name	Length	Type
sum (Unix)	16 or 32 bits	sum
sum8	8 bits	sum
sum16	16 bits	sum
sum24	24 bits	sum
sum32	32 bits	sum
fletcher-4	4 bits	sum
fletcher-8	8 bits	sum
fletcher-16	16 bits	sum
fletcher-32	32 bits	sum
Adler-32	32 bits	sum
xor8	8 bits	sum
Luhn algorithm	4 bits	sum
Verhoeff algorithm	4 bits	sum
Damm algorithm	1 decimal digit	Quasigroup operation

Non-cryptographic hash functions

Name	Length	Type
Pearson hashing	8 bits
Fowler–Noll–Vo hash function (FNV Hash)	32, 64, 128, 256, 512, or 1024 bits	xor/product or product/xor
Zobrist hashing	variable	xor
Jenkins hash function	32 or 64 bits	xor/addition
Java hashCode()	32 bits
Bernstein hash[1]	32 bits
elf64	64 bits	hash
MurmurHash	32, 64, or 128 bits	product/rotation
SpookyHash	128 bits	see Jenkins hash function
CityHash	64, 128, or 256 bits

Cryptographic hash functions

Main article: cryptographic hash function

Name	Length	Type
BLAKE-256	256 bits	HAIFA structure
BLAKE-512	512 bits	HAIFA structure
ECOH	224 to 512 bits	hash
FSB	160 to 512 bits	hash
GOST	256 bits	hash
Grøstl	256 to 512 bits	hash
HAS-160	160 bits	hash
HAVAL	128 to 256 bits	hash
JH	512 bits	hash
MD2	128 bits	hash
MD4	128 bits	hash
MD5	128 bits	Merkle-Damgård construction
MD6	512 bits	Merkle tree NLFSR
RadioGatún	Up to 1216 bits	hash
RIPEMD-64	64 bits	hash
RIPEMD-160	160 bits	hash
RIPEMD-320	320 bits	hash
SHA-1	160 bits	Merkle-Damgård construction
SHA-224	224 bits	Merkle-Damgård construction
SHA-256	256 bits	Merkle-Damgård construction
SHA-384	384 bits	Merkle-Damgård construction
SHA-512	512 bits	Merkle-Damgård construction
SHA-3 (originally known as Keccak)	arbitrary	Sponge function
Skein	arbitrary	Unique Block Iteration
SipHash	64 bits	non-collision-resistant PRF
Snefru	128 or 256 bits	hash
Spectral Hash	512 bits	Wide Pipe Merkle-Damgård construction
SWIFFT	512 bits	hash
Tiger	192 bits	hash
Whirlpool	512 bits	hash

Also see

• NIST hash function competition

Notes

1. ^ http://www.partow.net/programming/hashfunctions/index.html

Jenkins hash function

From Wikipedia, the free encyclopedia

Jump to: navigation, search

The Jenkins hash functions are a collection of (non-cryptographic) hash functions for multi-byte keys designed by Bob Jenkins. They can be used also as checksums to detect accidental data corruption or detect identical records in a database. The first one was formally published in 1997.

The hash functions

one-at-a-time

Jenkins's one-at-a-time hash is adapted here from a WWW page by Bob Jenkins,^[1] which is an expanded version of his Dr. Dobbs article.^[2]

uint32_t jenkins_one_at_a_time_hash(char *key, size_t len)
{
    uint32_t hash, i;
    for(hash = i = 0; i < len; ++i)
    {
        hash += key[i];
        hash += (hash << 10);
        hash ^= (hash >> 6);
    }
    hash += (hash << 3);
    hash ^= (hash >> 11);
    hash += (hash << 15);
    return hash;
}

Avalanche behavior of Jenkins One-at-a-time hash over 3-byte keys

The avalanche behavior of this hash is shown on the right.

Each of the 24 rows corresponds to a single bit in the 3-byte input key, and each of the 32 columns corresponds to a bit in the output hash. Colors are chosen by how well the input key bit affects the given output hash bit: a green square indicates good mixing behavior, a yellow square weak mixing behavior, and red would indicate no mixing. Only a few bits in the last byte of the input key are weakly mixed to a minority of bits in the output hash.

The standard implementation of the Perl programming language includes Jenkins's one-at-a-time hash and SipHash, and uses Jenkins's one-at-a-time hash by default.^[3][4][5]

lookup2

The lookup2 function was an interim successor to one-at-a-time. It is the function referred to as "My Hash" in the 1997 Dr. Dobbs journal article, though it has been obsoleted by subsequent functions that Jenkins has released.

lookup3

The lookup3 function consumes input in 12 byte (96 bit) chunks.^[6] It may be appropriate when speed is more important than simplicity. Note, though, that any speed improvement from the use of this hash is only likely to be useful for large keys, and that the increased complexity may also have speed consequences such as preventing an optimizing compiler from inlining the hash function.

SpookyHash

In 2011 Jenkins released a new 128-bit hash function called SpookyHash.^[7] SpookyHash is significantly faster than lookup3.

See also

• CityHash
• Fowler Noll Vo hash
• MurmurHash

References

1. ^ Jenkins, Bob (ca. 2006). "A hash function for hash Table lookup". Retrieved April 16, 2009.
2. ^ Jenkins, Bob (September 1997). "Hash functions". Dr. Dobbs Journal.
3. ^ "What hashing function/algorithm does Perl use ?"
4. ^ "RFC: perlfeaturedelta": "one-at-a-time hash algorithm ... [was added in version] 5.8.0"
5. ^ "perl: hv_func.h"
6. ^ Jenkins, Bob. "lookup3.c source code". Retrieved April 16, 2009.
7. ^ Jenkins, Bob. "SpookyHash: a 128-bit noncryptographic hash". Retrieved Jan 29, 2012.

Hash table

From Wikipedia, the free encyclopedia

Jump to: navigation, search

Not to be confused with Hash list or Hash tree.

Hash table
Type	Unordered associative array
Invented	1953
Time complexity in big O notation
	Average	Worst case
Space	O(n)[1]	O(n)
Search	O(1)	O(n)
Insert	O(1)	O(n)
Delete	O(1)	O(n)

A small phone book as a hash table

In computing, a hash table (also hash map) is a data structure used to implement an associative array, a structure that can map keys to values. A hash table uses a hash function to compute an index into an array of buckets or slots, from which the correct value can be found.

Ideally, the hash function should assign each possible key to a unique bucket, but this ideal situation is rarely achievable in practice (unless the hash keys are fixed; i.e. new entries are never added to the table after it is created). Instead, most hash table designs assume that hash collisions—different keys that are assigned by the hash function to the same bucket—will occur and must be accommodated in some way.

In a well-dimensioned hash table, the average cost (number of instructions) for each lookup is independent of the number of elements stored in the table. Many hash table designs also allow arbitrary insertions and deletions of key-value pairs, at (amortized^[2]) constant average cost per operation.^[3][4]

In many situations, hash tables turn out to be more efficient than search trees or any other table lookup structure. For this reason, they are widely used in many kinds of computer software, particularly for associative arrays, database indexing, caches, and sets.

Hashing

Main article: Hash function

The idea of hashing is to distribute the entries (key/value pairs) across an array of buckets. Given a key, the algorithm computes an index that suggests where the entry can be found:

 index = f(key, array_size)

Often this is done in two steps:

 hash = hashfunc(key)

 index = hash % array_size

In this method, the hash is independent of the array size, and it is then reduced to an index (a number between 0 and array_size − 1) using a remainder operation (%).

In the case that the array size is a power of two, the remainder operation is reduced to masking, which improves speed, but can increase problems with a poor hash function.

Choosing a good hash function

A good hash function and implementation algorithm are essential for good hash table performance, but may be difficult to achieve.

A basic requirement is that the function should provide a uniform distribution of hash values. A non-uniform distribution increases the number of collisions and the cost of resolving them. Uniformity is sometimes difficult to ensure by design, but may be evaluated empirically using statistical tests, e.g. a Pearson's chi-squared test for discrete uniform distributions ^{[5] [6]}

The distribution needs to be uniform only for table sizes s that occur in the application. In particular, if one uses dynamic resizing with exact doubling and halving of s, the hash function needs to be uniform only when s is a power of two. On the other hand, some hashing algorithms provide uniform hashes only when s is a prime number.^[7]

For open addressing schemes, the hash function should also avoid clustering, the mapping of two or more keys to consecutive slots. Such clustering may cause the lookup cost to skyrocket, even if the load factor is low and collisions are infrequent. The popular multiplicative hash^[3] is claimed to have particularly poor clustering behavior.^[7]

Cryptographic hash functions are believed to provide good hash functions for any table size s, either by modulo reduction or by bit masking. They may also be appropriate if there is a risk of malicious users trying to sabotage a network service by submitting requests designed to generate a large number of collisions in the server's hash tables. However, the risk of sabotage can also be avoided by cheaper methods (such as applying a secret salt to the data, or using a universal hash function).

Some authors claim that good hash functions should have the avalanche effect; that is, a single-bit change in the input key should affect, on average, half the bits in the output. Some popular hash functions do not have this property.^{[citation needed]}

Perfect hash function

If all keys are known ahead of time, a perfect hash function can be used to create a perfect hash table that has no collisions. If minimal perfect hashing is used, every location in the hash table can be used as well.

Perfect hashing allows for constant time lookups in the worst case. This is in contrast to most chaining and open addressing methods, where the time for lookup is low on average, but may be very large (proportional to the number of entries) for some sets of keys.

Key statistics

A critical statistic for a hash table is called the load factor. This is simply the number of entries divided by the number of buckets, that is, n/k where n is the number of entries and k is the number of buckets.

If the load factor is kept reasonable, the hash table should perform well, provided the hashing is good. If the load factor grows too large, the hash table will become slow, or it may fail to work (depending on the method used). The expected constant time property of a hash table assumes that the load factor is kept below some bound. For a fixed number of buckets, the time for a lookup grows with the number of entries and so does not achieve the desired constant time.

Second to that, one can examine the variance of number of entries per bucket. For example, two tables both have 1000 entries and 1000 buckets; one has exactly one entry in each bucket, the other has all entries in the same bucket. Clearly the hashing is not working in the second one.

A low load factor is not especially beneficial. As load factor approaches 0, the proportion of unused areas in the hash table increases, but there is not necessarily any reduction in search cost. This results in wasted memory.

Collision resolution

Hash collisions are practically unavoidable when hashing a random subset of a large set of possible keys. For example, if 2,500 keys are hashed into a million buckets, even with a perfectly uniform random distribution, according to the birthday problem there is a 95% chance of at least two of the keys being hashed to the same slot.

Therefore, most hash table implementations have some collision resolution strategy to handle such events. Some common strategies are described below. All these methods require that the keys (or pointers to them) be stored in the table, together with the associated values.

Separate chaining

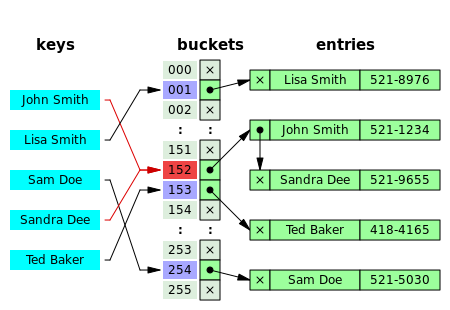
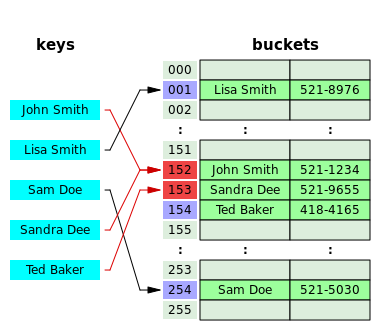
Hash collision resolved by separate chaining.

In the method known as separate chaining, each bucket is independent, and has some sort of list of entries with the same index. The time for hash table operations is the time to find the bucket (which is constant) plus the time for the list operation. (The technique is also called open hashing or closed addressing.)

In a good hash table, each bucket has zero or one entries, and sometimes two or three, but rarely more than that. Therefore, structures that are efficient in time and space for these cases are preferred. Structures that are efficient for a fairly large number of entries are not needed or desirable. If these cases happen often, the hashing is not working well, and this needs to be fixed.

Separate chaining with linked lists

Chained hash tables with linked lists are popular because they require only basic data structures with simple algorithms, and can use simple hash functions that are unsuitable for other methods.

The cost of a table operation is that of scanning the entries of the selected bucket for the desired key. If the distribution of keys is sufficiently uniform, the average cost of a lookup depends only on the average number of keys per bucket—that is, on the load factor.

Chained hash tables remain effective even when the number of table entries n is much higher than the number of slots. Their performance degrades more gracefully (linearly) with the load factor. For example, a chained hash table with 1000 slots and 10,000 stored keys (load factor 10) is five to ten times slower than a 10,000-slot table (load factor 1); but still 1000 times faster than a plain sequential list, and possibly even faster than a balanced search tree.

For separate-chaining, the worst-case scenario is when all entries are inserted into the same bucket, in which case the hash table is ineffective and the cost is that of searching the bucket data structure. If the latter is a linear list, the lookup procedure may have to scan all its entries, so the worst-case cost is proportional to the number n of entries in the table.

The bucket chains are often implemented as ordered lists, sorted by the key field; this choice approximately halves the average cost of unsuccessful lookups, compared to an unordered list^{[citation needed]}. However, if some keys are much more likely to come up than others, an unordered list with move-to-front heuristic may be more effective. More sophisticated data structures, such as balanced search trees, are worth considering only if the load factor is large (about 10 or more), or if the hash distribution is likely to be very non-uniform, or if one must guarantee good performance even in a worst-case scenario. However, using a larger table and/or a better hash function may be even more effective in those cases.

Chained hash tables also inherit the disadvantages of linked lists. When storing small keys and values, the space overhead of the next pointer in each entry record can be significant. An additional disadvantage is that traversing a linked list has poor cache performance, making the processor cache ineffective.

Separate chaining with list heads

Hash collision by separate chaining with head records in the bucket array.

Some chaining implementations store the first record of each chain in the slot array itself.^[4] The number of pointer traversals is decreased by one for most cases. The purpose is to increase cache efficiency of hash table access.

The disadvantage is that an empty bucket takes the same space as a bucket with one entry. To save memory space, such hash tables often have about as many slots as stored entries, meaning that many slots have two or more entries.

Separate chaining with other structures

Instead of a list, one can use any other data structure that supports the required operations. For example, by using a self-balancing tree, the theoretical worst-case time of common hash table operations (insertion, deletion, lookup) can be brought down to O(log n) rather than O(n). However, this approach is only worth the trouble and extra memory cost if long delays must be avoided at all costs (e.g. in a real-time application), or if one must guard against many entries hashed to the same slot (e.g. if one expects extremely non-uniform distributions, or in the case of web sites or other publicly accessible services, which are vulnerable to malicious key distributions in requests).

The variant called array hash table uses a dynamic array to store all the entries that hash to the same slot.^[8][9][10] Each newly inserted entry gets appended to the end of the dynamic array that is assigned to the slot. The dynamic array is resized in an exact-fit manner, meaning it is grown only by as many bytes as needed. Alternative techniques such as growing the array by block sizes or pages were found to improve insertion performance, but at a cost in space. This variation makes more efficient use of CPU caching and the translation lookaside buffer (TLB), because slot entries are stored in sequential memory positions. It also dispenses with the next pointers that are required by linked lists, which saves space. Despite frequent array resizing, space overheads incurred by operating system such as memory fragmentation, were found to be small.

An elaboration on this approach is the so-called dynamic perfect hashing,^[11] where a bucket that contains k entries is organized as a perfect hash table with k² slots. While it uses more memory (n² slots for n entries, in the worst case and n*k slots in the average case), this variant has guaranteed constant worst-case lookup time, and low amortized time for insertion.

Open addressing

Hash collision resolved by open addressing with linear probing (interval=1). Note that "Ted Baker" has a unique hash, but nevertheless collided with "Sandra Dee", that had previously collided with "John Smith".

In another strategy, called open addressing, all entry records are stored in the bucket array itself. When a new entry has to be inserted, the buckets are examined, starting with the hashed-to slot and proceeding in some probe sequence, until an unoccupied slot is found. When searching for an entry, the buckets are scanned in the same sequence, until either the target record is found, or an unused array slot is found, which indicates that there is no such key in the table.^[12] The name "open addressing" refers to the fact that the location ("address") of the item is not determined by its hash value. (This method is also called closed hashing; it should not be confused with "open hashing" or "closed addressing" that usually mean separate chaining.)

Well-known probe sequences include:

• Linear probing, in which the interval between probes is fixed (usually 1)
• Quadratic probing, in which the interval between probes is increased by adding the successive outputs of a quadratic polynomial to the starting value given by the original hash computation
• Double hashing, in which the interval between probes is computed by another hash function

A drawback of all these open addressing schemes is that the number of stored entries cannot exceed the number of slots in the bucket array. In fact, even with good hash functions, their performance dramatically degrades when the load factor grows beyond 0.7 or so. Thus a more aggressive resize scheme is needed. Separate linking works correctly with any load factor, although performance is likely to be reasonable if it is kept below 2 or so. For many applications, these restrictions mandate the use of dynamic resizing, with its attendant costs.

Open addressing schemes also put more stringent requirements on the hash function: besides distributing the keys more uniformly over the buckets, the function must also minimize the clustering of hash values that are consecutive in the probe order. Using separate chaining, the only concern is that too many objects map to the same hash value; whether they are adjacent or nearby is completely irrelevant.

Open addressing only saves memory if the entries are small (less than four times the size of a pointer) and the load factor is not too small. If the load factor is close to zero (that is, there are far more buckets than stored entries), open addressing is wasteful even if each entry is just two words.

This graph compares the average number of cache misses required to look up elements in tables with chaining and linear probing. As the table passes the 80%-full mark, linear probing's performance drastically degrades.

Open addressing avoids the time overhead of allocating each new entry record, and can be implemented even in the absence of a memory allocator. It also avoids the extra indirection required to access the first entry of each bucket (that is, usually the only one). It also has better locality of reference, particularly with linear probing. With small record sizes, these factors can yield better performance than chaining, particularly for lookups.

Hash tables with open addressing are also easier to serialize, because they do not use pointers.

On the other hand, normal open addressing is a poor choice for large elements, because these elements fill entire CPU cache lines (negating the cache advantage), and a large amount of space is wasted on large empty table slots. If the open addressing table only stores references to elements (external storage), it uses space comparable to chaining even for large records but loses its speed advantage.

Generally speaking, open addressing is better used for hash tables with small records that can be stored within the table (internal storage) and fit in a cache line. They are particularly suitable for elements of one word or less. If the table is expected to have a high load factor, the records are large, or the data is variable-sized, chained hash tables often perform as well or better.

Ultimately, used sensibly, any kind of hash table algorithm is usually fast enough; and the percentage of a calculation spent in hash table code is low. Memory usage is rarely considered excessive. Therefore, in most cases the differences between these algorithms are marginal, and other considerations typically come into play.^{[citation needed]}

Coalesced hashing

A hybrid of chaining and open addressing, coalesced hashing links together chains of nodes within the table itself.^[12] Like open addressing, it achieves space usage and (somewhat diminished) cache advantages over chaining. Like chaining, it does not exhibit clustering effects; in fact, the table can be efficiently filled to a high density. Unlike chaining, it cannot have more elements than table slots.

Cuckoo hashing

Another alternative open-addressing solution is cuckoo hashing, which ensures constant lookup time in the worst case, and constant amortized time for insertions and deletions. It uses two or more hash functions, which means any key/value pair could be in two or more locations. For lookup, the first hash function is used; if the key/value is not found, then the second hash function is used, and so on. If a collision happens during insertion, then the key is re-hashed with the second hash function to map it to another bucket. If all hash functions are used and there is still a collision, then the key it collided with is removed to make space for the new key, and the old key is re-hashed with one of the other hash functions, which maps it to another bucket. If that location also results in a collision, then the process repeats until there is no collision or the process traverses all the buckets, at which point the table is resized. By combining multiple hash functions with multiple cells per bucket, very high space utilisation can be achieved.

Robin Hood hashing

One interesting variation on double-hashing collision resolution is Robin Hood hashing.^[13] The idea is that a new key may displace a key already inserted, if its probe count is larger than that of the key at the current position. The net effect of this is that it reduces worst case search times in the table. This is similar to Knuth's ordered hash tables except that the criterion for bumping a key does not depend on a direct relationship between the keys. Since both the worst case and the variation in the number of probes is reduced dramatically, an interesting variation is to probe the table starting at the expected successful probe value and then expand from that position in both directions.^[14] External Robin Hashing is an extension of this algorithm where the table is stored in an external file and each table position corresponds to a fixed-sized page or bucket with B records.^[15]

2-choice hashing

2-choice hashing employs 2 different hash functions, h₁(x) and h₂(x), for the hash table. Both hash functions are used to compute two table locations. When an object is inserted in the table, then it is placed in the table location that contains fewer objects (with the default being the h₁(x) table location if there is equality in bucket size). 2-choice hashing employs the principle of the power of two choices.

Hopscotch hashing

Another alternative open-addressing solution is hopscotch hashing,^[16] which combines the approaches of cuckoo hashing and linear probing, yet seems in general to avoid their limitations. In particular it works well even when the load factor grows beyond 0.9. The algorithm is well suited for implementing a resizable concurrent hash table.

The hopscotch hashing algorithm works by defining a neighborhood of buckets near the original hashed bucket, where a given entry is always found. Thus, search is limited to the number of entries in this neighborhood, which is logarithmic in the worst case, constant on average, and with proper alignment of the neighborhood typically requires one cache miss. When inserting an entry, one first attempts to add it to a bucket in the neighborhood. However, if all buckets in this neighborhood are occupied, the algorithm traverses buckets in sequence until an open slot (an unoccupied bucket) is found (as in linear probing). At that point, since the empty bucket is outside the neighborhood, items are repeatedly displaced in a sequence of hops. (This is similar to cuckoo hashing, but with the difference that in this case the empty slot is being moved into the neighborhood, instead of items being moved out with the hope of eventually finding an empty slot.) Each hop brings the open slot closer to the original neighborhood, without invalidating the neighborhood property of any of the buckets along the way. In the end, the open slot has been moved into the neighborhood, and the entry being inserted can be added to it.

Dynamic resizing

To keep the load factor under a certain limit, e.g. under 3/4, many table implementations expand the table when items are inserted. For example, in Java's HashMap class the default load factor threshold for table expansion is 0.75.

Since buckets are usually implemented on top of a dynamic array and any constant proportion for resizing greater than 1 will keep the load factor under the desired limit, the exact choice of the constant is determined by the same space-time tradeoff as for dynamic arrays.

Resizing is accompanied by a full or incremental table rehash whereby existing items are mapped to new bucket locations.

To limit the proportion of memory wasted due to empty buckets, some implementations also shrink the size of the table—followed by a rehash—when items are deleted. From the point of space-time tradeoffs, this operation is similar to the deallocation in dynamic arrays.

Resizing by copying all entries

A common approach is to automatically trigger a complete resizing when the load factor exceeds some threshold r_max. Then a new larger table is allocated, all the entries of the old table are removed and inserted into this new table, and the old table is returned to the free storage pool. Symmetrically, when the load factor falls below a second threshold r_min, all entries are moved to a new smaller table.

If the table size increases or decreases by a fixed percentage at each expansion, the total cost of these resizings, amortized over all insert and delete operations, is still a constant, independent of the number of entries n and of the number m of operations performed.

For example, consider a table that was created with the minimum possible size and is doubled each time the load ratio exceeds some threshold. If m elements are inserted into that table, the total number of extra re-insertions that occur in all dynamic resizings of the table is at most m − 1. In other words, dynamic resizing roughly doubles the cost of each insert or delete operation.

Incremental resizing

Some hash table implementations, notably in real-time systems, cannot pay the price of enlarging the hash table all at once, because it may interrupt time-critical operations. If one cannot avoid dynamic resizing, a solution is to perform the resizing gradually:

• During the resize, allocate the new hash table, but keep the old table unchanged.
• In each lookup or delete operation, check both tables.
• Perform insertion operations only in the new table.
• At each insertion also move r elements from the old table to the new table.
• When all elements are removed from the old table, deallocate it.

To ensure that the old table is completely copied over before the new table itself needs to be enlarged, it is necessary to increase the size of the table by a factor of at least (r + 1)/r during resizing.

Monotonic keys

If it is known that key values will always increase (or decrease) monotonically, then a variation of consistent hashing can be achieved by keeping a list of the single most recent key value at each hash table resize operation. Upon lookup, keys that fall in the ranges defined by these list entries are directed to the appropriate hash function—and indeed hash table—both of which can be different for each range. Since it is common to grow the overall number of entries by doubling, there will only be O(lg(N)) ranges to check, and binary search time for the redirection would be O(lg(lg(N))). As with consistent hashing, this approach guarantees that any key's hash, once issued, will never change, even when the hash table is later grown.

Other solutions

Linear hashing^[17] is a hash table algorithm that permits incremental hash table expansion. It is implemented using a single hash table, but with two possible look-up functions.

Another way to decrease the cost of table resizing is to choose a hash function in such a way that the hashes of most values do not change when the table is resized. This approach, called consistent hashing, is prevalent in disk-based and distributed hashes, where rehashing is prohibitively costly.

Performance analysis

In the simplest model, the hash function is completely unspecified and the table does not resize. For the best possible choice of hash function, a table of size k with open addressing has no collisions and holds up to k elements, with a single comparison for successful lookup, and a table of size k with chaining and n keys has the minimum max(0, n-k) collisions and O(1 + n/k) comparisons for lookup. For the worst choice of hash function, every insertion causes a collision, and hash tables degenerate to linear search, with Ω(n) amortized comparisons per insertion and up to n comparisons for a successful lookup.

Adding rehashing to this model is straightforward. As in a dynamic array, geometric resizing by a factor of b implies that only n/bⁱ keys are inserted i or more times, so that the total number of insertions is bounded above by bn/(b-1), which is O(n). By using rehashing to maintain n < k, tables using both chaining and open addressing can have unlimited elements and perform successful lookup in a single comparison for the best choice of hash function.

In more realistic models, the hash function is a random variable over a probability distribution of hash functions, and performance is computed on average over the choice of hash function. When this distribution is uniform, the assumption is called "simple uniform hashing" and it can be shown that hashing with chaining requires Θ(1 + n/k) comparisons on average for an unsuccessful lookup, and hashing with open addressing requires Θ(1/(1 - n/k)).^[18] Both these bounds are constant, if we maintain n/k < c using table resizing, where c is a fixed constant less than 1.

Features

Advantages

The main advantage of hash tables over other table data structures is speed. This advantage is more apparent when the number of entries is large. Hash tables are particularly efficient when the maximum number of entries can be predicted in advance, so that the bucket array can be allocated once with the optimum size and never resized.

If the set of key-value pairs is fixed and known ahead of time (so insertions and deletions are not allowed), one may reduce the average lookup cost by a careful choice of the hash function, bucket table size, and internal data structures. In particular, one may be able to devise a hash function that is collision-free, or even perfect (see below). In this case the keys need not be stored in the table.

Drawbacks

Although operations on a hash table take constant time on average, the cost of a good hash function can be significantly higher than the inner loop of the lookup algorithm for a sequential list or search tree. Thus hash tables are not effective when the number of entries is very small. (However, in some cases the high cost of computing the hash function can be mitigated by saving the hash value together with the key.)

For certain string processing applications, such as spell-checking, hash tables may be less efficient than tries, finite automata, or Judy arrays. Also, if each key is represented by a small enough number of bits, then, instead of a hash table, one may use the key directly as the index into an array of values. Note that there are no collisions in this case.

The entries stored in a hash table can be enumerated efficiently (at constant cost per entry), but only in some pseudo-random order. Therefore, there is no efficient way to locate an entry whose key is nearest to a given key. Listing all n entries in some specific order generally requires a separate sorting step, whose cost is proportional to log(n) per entry. In comparison, ordered search trees have lookup and insertion cost proportional to log(n), but allow finding the nearest key at about the same cost, and ordered enumeration of all entries at constant cost per entry.

If the keys are not stored (because the hash function is collision-free), there may be no easy way to enumerate the keys that are present in the table at any given moment.

Although the average cost per operation is constant and fairly small, the cost of a single operation may be quite high. In particular, if the hash table uses dynamic resizing, an insertion or deletion operation may occasionally take time proportional to the number of entries. This may be a serious drawback in real-time or interactive applications.

Hash tables in general exhibit poor locality of reference—that is, the data to be accessed is distributed seemingly at random in memory. Because hash tables cause access patterns that jump around, this can trigger microprocessor cache misses that cause long delays. Compact data structures such as arrays searched with linear search may be faster, if the table is relatively small and keys are integers or other short strings. According to Moore's Law, cache sizes are growing exponentially and so what is considered "small" may be increasing. The optimal performance point varies from system to system.

Hash tables become quite inefficient when there are many collisions. While extremely uneven hash distributions are extremely unlikely to arise by chance, a malicious adversary with knowledge of the hash function may be able to supply information to a hash that creates worst-case behavior by causing excessive collisions, resulting in very poor performance, e.g. a denial of service attack.^[19] In critical applications, universal hashing can be used; a data structure with better worst-case guarantees may be preferable.^[20]

Uses

This section does not cite any references or sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (July 2013)

Associative arrays

Hash tables are commonly used to implement many types of in-memory tables. They are used to implement associative arrays (arrays whose indices are arbitrary strings or other complicated objects), especially in interpreted programming languages like AWK, Perl, and PHP.

When storing a new item into a multimap and a hash collision occurs, the multimap unconditionally stores both items.

When storing a new item into a typical associative array and a hash collision occurs, but the actual keys themselves are different, the associative array likewise stores both items. However, if the key of the new item exactly matches the key of an old item, the associative array typically erases the old item and overwrites it with the new item, so every item in the table has a unique key.

Database indexing

Hash tables may also be used as disk-based data structures and database indices (such as in dbm) although B-trees are more popular in these applications.

Caches

Hash tables can be used to implement caches, auxiliary data tables that are used to speed up the access to data that is primarily stored in slower media. In this application, hash collisions can be handled by discarding one of the two colliding entries—usually erasing the old item that is currently stored in the table and overwriting it with the new item, so every item in the table has a unique hash value.

Sets

Besides recovering the entry that has a given key, many hash table implementations can also tell whether such an entry exists or not.

Those structures can therefore be used to implement a set data structure, which merely records whether a given key belongs to a specified set of keys. In this case, the structure can be simplified by eliminating all parts that have to do with the entry values. Hashing can be used to implement both static and dynamic sets.

Object representation

Several dynamic languages, such as Perl, Python, JavaScript, and Ruby, use hash tables to implement objects. In this representation, the keys are the names of the members and methods of the object, and the values are pointers to the corresponding member or method.

Unique data representation

Hash tables can be used by some programs to avoid creating multiple character strings with the same contents. For that purpose, all strings in use by the program are stored in a single hash table, which is checked whenever a new string has to be created. This technique was introduced in Lisp interpreters under the name hash consing, and can be used with many other kinds of data (expression trees in a symbolic algebra system, records in a database, files in a file system, binary decision diagrams, etc.)

String interning

Main article: String interning

Implementations

In programming languages

Many programming languages provide hash table functionality, either as built-in associative arrays or as standard library modules. In C++11, for example, the unordered_map class provides hash tables for keys and values of arbitrary type.

In PHP 5, the Zend 2 engine uses one of the hash functions from Daniel J. Bernstein to generate the hash values used in managing the mappings of data pointers stored in a hash table. In the PHP source code, it is labelled as DJBX33A (Daniel J. Bernstein, Times 33 with Addition).

Python's built-in hash table implementation, in the form of the dict type, as well as Perl's hash type (%) are highly optimized as they are used internally to implement namespaces.

In the .NET Framework, support for hash tables is provided via the non-generic Hashtable and generic Dictionary classes, which store key-value pairs, and the generic HashSet class, which stores only values.

Independent packages

• SparseHash (formerly Google SparseHash) An extremely memory-efficient hash_map implementation, with only 2 bits/entry of overhead. The SparseHash library has several C++ hash map implementations with different performance characteristics, including one that optimizes for memory use and another that optimizes for speed.
• SunriseDD An open source C library for hash table storage of arbitrary data objects with lock-free lookups, built-in reference counting and guaranteed order iteration. The library can participate in external reference counting systems or use its own built-in reference counting. It comes with a variety of hash functions and allows the use of runtime supplied hash functions via callback mechanism. Source code is well documented.
• uthash This is an easy-to-use hash table for C structures.

History

The idea of hashing arose independently in different places. In January 1953, H. P. Luhn wrote an internal IBM memorandum that used hashing with chaining.^[21] G. N. Amdahl, E. M. Boehme, N. Rochester, and Arthur Samuel implemented a program using hashing at about the same time. Open addressing with linear probing (relatively prime stepping) is credited to Amdahl, but Ershov (in Russia) had the same idea.^[21]

See also

• Rabin–Karp string search algorithm
• Stable hashing
• Consistent hashing
• Extendible hashing
• Lazy deletion
• Pearson hashing

Related data structures

There are several data structures that use hash functions but cannot be considered special cases of hash tables:

• Bloom filter, memory efficient data-structure designed for constant-time approximate lookups; uses hash function(s) and can be seen as an approximate hash table.
• Distributed hash table (DHT), a resilient dynamic table spread over several nodes of a network.
• Hash array mapped trie, a trie structure, similar to the array mapped trie, but where each key is hashed first.

References

1. ^ Thomas H. Cormen [et al.] (2009). Introduction to Algorithms (3rd ed.). Massachusetts Institute of Technology. pp. 253–280. ISBN 978-0-262-03384-8. Unknown parameter |note= ignored (help)
2. ^ Charles E. Leiserson, Amortized Algorithms, Table Doubling, Potential Method Lecture 13, course MIT 6.046J/18.410J Introduction to Algorithms—Fall 2005
3. ^ ^{a b} Donald Knuth (1998). 'The Art of Computer Programming'. 3: Sorting and Searching (2nd ed.). Addison-Wesley. pp. 513–558. ISBN 0-201-89685-0. Unknown parameter |note= ignored (help)
4. ^ ^{a b} Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001). Introduction to Algorithms (2nd ed.). MIT Press and McGraw-Hill. 221–252. ISBN 978-0-262-53196-2.
5. ^ Karl Pearson (1900). "On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling". Philosophical Magazine, Series 5 50 (302). pp. 157–175.
6. ^ Robin Plackett (1983). "Karl Pearson and the Chi-Squared Test". International Statistical Review (International Statistical Institute (ISI)) 51 (1). pp. 59–72.
7. ^ ^{a b} Thomas Wang (1997), Prime Double Hash Table. Retrieved April 27, 2012
8. ^ Askitis, Nikolas; Zobel, Justin (October 2005). "Cache-conscious Collision Resolution in String Hash Tables". Proceedings of the 12th International Conference, String Processing and Information Retrieval (SPIRE 2005). 3772/2005. pp. 91–102. doi:10.1007/11575832_11. ISBN 978-3-540-29740-6.
9. ^ Askitis, Nikolas; Sinha, Ranjan (2010). "Engineering scalable, cache and space efficient tries for strings". The VLDB Journal 17 (5): 633–660. doi:10.1007/s00778-010-0183-9. ISSN 1066-8888.
10. ^ Askitis, Nikolas (2009). "Fast and Compact Hash Tables for Integer Keys". Proceedings of the 32nd Australasian Computer Science Conference (ACSC 2009) 91. pp. 113–122. ISBN 978-1-920682-72-9.
11. ^ Erik Demaine, Jeff Lind. 6.897: Advanced Data Structures. MIT Computer Science and Artificial Intelligence Laboratory. Spring 2003. http://courses.csail.mit.edu/6.897/spring03/scribe_notes/L2/lecture2.pdf
12. ^ ^{a b} Tenenbaum, Aaron M.; Langsam, Yedidyah; Augenstein, Moshe J. (1990). Data Structures Using C. Prentice Hall. pp. 456–461, p. 472. ISBN 0-13-199746-7.
13. ^ Celis, Pedro (1986). Robin Hood hashing (Technical report CS-86-14). Computer Science Department, University of Waterloo.
14. ^ Viola, Alfredo (October 2005). "Exact distribution of individual displacements in linear probing hashing". Transactions on Algorithms (TALG) (ACM) 1 (2,): 214–242. doi:10.1145/1103963.1103965.
15. ^ Celis, Pedro (March 1988). External Robin Hood Hashing (Technical report TR246). Computer Science Department, Indiana University.
16. ^ Herlihy, Maurice and Shavit, Nir and Tzafrir, Moran (2008). "Hopscotch Hashing". DISC '08: Proceedings of the 22nd international symposium on Distributed Computing. Arcachon, France: Springer-Verlag. pp. 350–364. Unknown parameter |address= ignored (help)
17. ^ Litwin, Witold (1980). "Linear hashing: A new tool for file and table addressing". Proc. 6th Conference on Very Large Databases. pp. 212–223.
18. ^ Doug Dunham. CS 4521 Lecture Notes. University of Minnesota Duluth. Theorems 11.2, 11.6. Last modified April 21, 2009.
19. ^ Alexander Klink and Julian Wälde's Efficient Denial of Service Attacks on Web Application Platforms, December 28, 2011, 28th Chaos Communication Congress. Berlin, Germany.
20. ^ Crosby and Wallach's Denial of Service via Algorithmic Complexity Attacks.
21. ^ ^{a b} Mehta, Dinesh P.; Sahni, Sartaj. Handbook of Datastructures and Applications. pp. 9–15. ISBN 1-58488-435-5.

Further reading

Tamassia, Roberto; Michael T. Goodrich (2006). "Chapter Nine: Maps and Dictionaries". Data structures and algorithms in Java : [updated for Java 5.0] (4th ed.). Hoboken, N.J.: Wiley. pp. 369–418. ISBN 0-471-73884-0.

McKenzie, B. J.; R. Harries, T.Bell (Feb 1990). "Selecting a hashing algorithm". Software -- Practice & Experience 20 (2): 209–224.

External links

Wikimedia Commons has media related to: Hash tables

• A Hash Function for Hash Table Lookup by Bob Jenkins.
• Hash Tables by SparkNotes—explanation using C
• Hash functions by Paul Hsieh
• Design of Compact and Efficient Hash Tables for Java link not working
• Libhashish hash library
• NIST entry on hash tables
• Open addressing hash table removal algorithm from ICI programming language, ici_set_unassign in set.c (and other occurrences, with permission).
• A basic explanation of how the hash table works by Reliable Software
• Lecture on Hash Tables
• Hash-tables in C—two simple and clear examples of hash tables implementation in C with linear probing and chaining
• Open Data Structures - Chapter 5 - Hash Tables
• MIT's Introduction to Algorithms: Hashing 1 MIT OCW lecture Video
• MIT's Introduction to Algorithms: Hashing 2 MIT OCW lecture Video
• How to sort a HashMap (Java) and keep the duplicate entries