原地归并

问题I:

传统归并排序需要O(n)的空间发杂度，但是否能够实现原地归并排序呢？即O（1）的空间复杂度。时间复杂度还是否是O（nlogn）？

对于这个问题，网上有很多资料，讲的比较清楚的有下面这个文章：

http://www.ahathinking.com/archives/103.html

在了解原地归并的思想之前，先回忆一下一般的归并算法，先是将有序子序列分别放入临时数组，然后设置两个指针依次从两个子序列的开始寻找最小元素放入归并数组中；那么原地归并的思想亦是如此，就是归并时要保证指针i之前的数字始终是两个子序列中最小的那些元素。文字叙述多了无用，见示例图解，一看就明白。

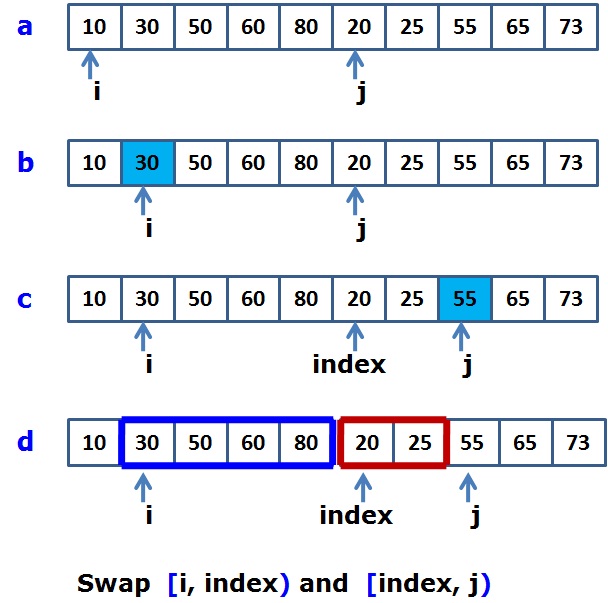
假设我们现在有两个有序子序列如图a，进行原地合并的图解示例如图b开始

如图b，首先第一个子序列的值与第二个子序列的第一个值20比较，如果序列一的值小于20，则指针i向后移，直到找到比20大的值，即指针i移动到30；经过b，我们知道指针i之前的值一定是两个子序列中最小的块。

如图c，先用一个临时指针记录j的位置，然后用第二个子序列的值与序列一i所指的值30比较，如果序列二的值小于30，则j后移，直到找到比30大的值，即j移动到55的下标；

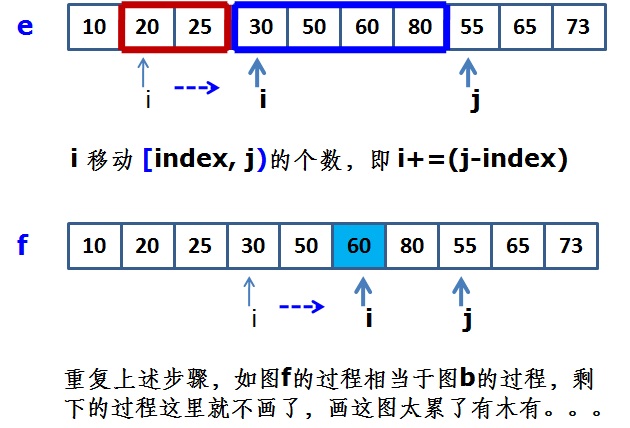
如图d，经过图c的过程，我们知道数组块 [index, j) 中的值一定是全部都小于指针i所指的值30，即数组块 [index, j) 中的值全部小于数组块 [i, index) 中的值，为了满足原地归并的原则：始终保证指针i之前的元素为两个序列中最小的那些元素，即i之前为已经归并好的元素。我们交换这两块数组的内存块，交换后i移动相应的步数，这个“步数”实际就是该步归并好的数值个数，即数组块[index, j)的个数。从而得到图e如下：

重复上述的过程，如图f，相当于图b的过程，直到最后，这就是原地归并的一种实现思想。

这里A、B两块的交换，可以通过对A翻转变为A‘，对B翻转变为B’，再对A‘B'翻转来求得。

上面的算法空间复杂度确实O（1），但时间复杂度就不再是O（nlogn）了，不知道是否有更好的原地快排？（注意：这里指的是对数组归并，不是链表）

此算法最坏的情况就是对[1,3,5,7,9,11]和 [2,4,6,8,10,12]类型的数据进行原地归并，就需要O（n^2）的时间复杂度。

问题II：

输入数组[a1,a2,...,an,b1,b2,...,bn]，做最少的操作，使得输出为，[a1,b1,a2,b2,...,an,bn]，注意：方法要是in-place的。

分析I：

这个问题正好是上面“原地归并”的最坏的情况，可以用上面的方法求解，但时间复杂度是O（n^2），其实，也就变成了插入排序了：

a1,a2,...,an的相对位置是对的，不需要做插入排序，

对b1，将b1向前移动n-1个位置，即插入到正确位置。

对b2，将b2向前移动n-2个位置，即插入到正确位置。

依次对b3,..bn做相同的操作（插入排序），即可得到要求的输出。

时间复杂度仍然是O（n^2）

分析II：

利用快排的思想：

假设区间由4段组成【A1，A2，B1，B2】。这里：

A1，A2分别对应于原来a1,a2,...,an的前半段和后半段。

B1，B2分别对应于原来b1,b2,...,bn的前半段和后半段。

将A2、B1交换位置，变为【A1，B1，A2，B2】。

这样，就可将问题转化为对【A1，B1】和【A2，B2】分别处理的两个子问题。

这样递归地求解下去，就可in-place地得到所要求的输出。

此算法的本质是快排，时间复杂度O（nlogn）。

分析III：

循环将元素放到最终的位置上，即

将a2放到a3的位置，将a3放到a5的位置，将a5放到a9的位置，这样依次做下去，直到所有元素都放到最终位置。

但对有些数据不是一个circle就可以解决的，如对下图A中的数据：

a2放到a3的位置，a3放到a5的位置，a5放到b4的位置，b4放到b3的位置，b3放到b1的位置，b1放到a2的位置，这是一个circle。经过这个circle的处理，序列变为图B所示，彩色元素均已交换过，即已经在最终位置了。但是还有部分元素没有处理，还需要对剩下的元素做循环shift的处理。

但，问题是：如何判断一个元素有没有在最终位置上，其实就是如何判找出下一个circle的起始位置。

这就需要对每个元素做标记（用位存储），需要O（n）的空间复杂度。

此算法的时间复杂度为O（n），空间复杂度为O（n）。

特殊情况：如果要处理的数据比较特殊，比如处理的是都大于零的数，那么：

将每个放到最终位置的元素取反，这样就可以通过元素的正负来判断是否在最终位置。

当所有元素都在最终位置上时，所有元素都被取反了。

然后再将每个元素取反，变回原来的值，就得到所要求的输出了，

时间复杂度为O（n），空间复杂度仅为O（1）。

分析IV：

在分析III中，由于需要找出下一个circle的起始位置，所以用了O（n）的空间复杂度。

其实，下一个circle的起始位置可以在常数时间内找出，不需要额外的存储空间。

具体分析，可参考以下资料：

参考论文：A Simple In-Place Algorithm for In-Shuffle

参考资料：http://www.newsmth.net/bbscon.php?bid=1032&id=47005

稍有不同的是，论文中处理的数组下标从1开始，而且每个元素都会移动位置。

其实，只要如下图所示：去掉两端元素，仅处理中间元素；这样就将问题转化为论文中的问题了。

算法的本质就要是运用数论的知识，找出规律：当2n=3^k-1时，每个circle的起始位置都为3^i。

然后，对于任意数组，只需将其分成若干满足2n=3^k-1的子数组，每个子数组单独处理即可。

算法流程：

时间复杂度O（n），空间复杂度O（1）

代码实现：

void rightShift(vector<int>::iterator it, int n, int m){
	reverse(it, it + (n - m));
	reverse(it + (n - m), it + n);
	reverse(it, it + n);
}
void circleShift(vector<int>::iterator it, int n){
	for(int i = 1; i <= n; i *= 3){
		int next = i * 2 % (2 * n + 1);
		int tmp = *(it + i - 1);
		while(true){
			swap(tmp, *(it + next -1));
			if(next == i)
				break;
			next = (next * 2) % (2 * n + 1);
		}
	}
}
void merger(vector<int>::iterator it, int n){
	int m = 0, tmp = 1;
	while(tmp * 3 - 1 <= 2 * n){
		m = (tmp * 3 - 1) / 2;
		tmp *= 3;
	}
	if(m == n){
		circleShift(it, n);
		return;
	}
	rightShift(it + m, n, m);
	circleShift(it, m);
	merger(it + 2 * m, n - m);
}

测试代码：

int main() {
	int n = 7;
	vector<int> v(2*n);
	for(int i = 0; i < n; ++i)
		v[i] = 2 * i;
	for(int i = n; i < 2*n; ++i)
		v[i] = 2 * (i - n) + 1;
	merger(v.begin()+1, n -1);
	for(auto i : v)
		cout << i << " ";
	cout << endl;
	return 0;
}