2.6.6制药CMC统计应用之预测区间与耐受区间

本文是《Statistical Applications for Chemistry Manufacturing and Controls CMC in the Pharmaceutical Industry》第2章2.6.6~2.6.7节的python解决方案

2.6.6下一观测值的预测区间

下一观测值的100（1-α）%双侧置预测区间的计算公式为：

以表01的8批药品的纯度数据为例，

用表2.10的统计量计算95%双侧预测区间为：

import numpy as np

from scipy import stats

y1 = [94.20,92.68,94.47,94.14,95.17,94.47,94.14,95.17]

x1 = [1,2,3,4,5,6,7,8]

n1 =len(y1)

x1_mean=np.mean(y1)

sv1=np.var(y1)*n1/(n1-1)

L=x1_mean-stats.t(n1-1).ppf(0.975)*((1+1/n1)*sv1)**0.5

U=x1_mean+stats.t(n1-1).ppf(0.975)*((1+1/n1)*sv1)**0.5

>>> L

92.3491245044999

>>> U

96.26087549550012

用t1-α/2:n-1替代等式（2.21）中的t1-α/2:n-1可以计算包含m个未来值的具有指定的置信水平的预测区间。如果m很大时，用下一节介绍的耐受区间更有用。

2.6.8未来值的耐受区间

双侧耐受区间是一种耐受区间希望包含总体最低100P%具有100（1-α）%置信系数。例如，如果P=0.99，α=0:05，我们可以说有95%的信心说99%的总体将落在计算的区间内。对于模型（2.7),双侧耐受区间为:

其中，和S2由表2.9确定。K值是常数从统计软件得到或查表得到。

n=8时查表得包含99%的95%耐受区间的K值为K =4:889。

使用这个K值和表2.10，

因此有95%的信心希望90.49 到 98.12%会包含99%的未来值。

有多种方法简单的近似K值。Howe (1969)的很好的近似为

其中χ2α:ν是自由度为ν，左边面积为α的卡方分位数。Z2 (1+P）/2是正态分位数，左边的面积为（1 + P）=2。项ne是用于预测的样本数，即有效样本数n，ν=n-1。本例K的近似为

这与准确的K值4.889很接近。

某公司在爱尔兰的工厂生产的8批药品的纯度数据如下，计算未来所有值的的100（1-α）%双侧耐受区间为：

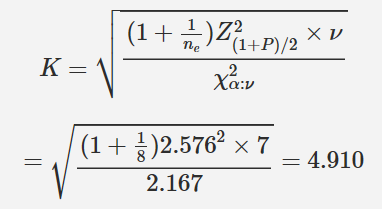
import numpy as np

from scipy import stats

y1 = [94.20,92.68,94.47,94.14,95.17,94.47,94.14,95.17]

x1 = [1,2,3,4,5,6,7,8]

n1 =len(y1)

x1_mean=np.mean(y1)

sv1=np.var(y1)*n1/(n1-1)

K=4.889

L=x1_mean-K*(sv1**0.5)

U=x1_mean+K*(sv1**0.5)

L

U

>>> L

90.49238596429096

>>> U

98.11761403570905

import numpy as np

from scipy import stats

y1 = [94.20,92.68,94.47,94.14,95.17,94.47,94.14,95.17]

x1 = [1,2,3,4,5,6,7,8]

n1 =len(y1)

ne=n1

x1_mean=np.mean(y1)

sv1=np.var(y1)*n1/(n1-1)

ne=n1

v=n1-1

P=0.99

a=0.05

K=(((1+1/ne)*(stats.norm.ppf((1+P)/2)**2)*v)/stats.chi2(v).ppf(a))**0.5

>>> K

4.909958765048029

如本例所示，最典型的是，ne等于样本量n，而ν等于n - 1。但是并不总是这样。在第9章给出一个例子，区间的中心用样本量为n1的数据集的均值，标准偏差为这个数据集为样本量为n2的数据集的联合方差估计。这种情况，ne=n1，ν=n1 + n2 -2。

有时候只需要计算单侧置信带。典型的，希望下侧耐受区带被总体100P%超过，或者上耐受带超过总体最少100P%，P> 0:5。准确耐受带可以用非中心t分布计算。

占总体的至少100P%的100（1-α）%下侧耐受带为:

其中t1-α:n1, ncp是非中心t分布的分位数，左边的面积为1-α，自由度为n-1，非中心参数为ncp，ZP是标准正态分位数左边的面积为P。占总体的至少100P%的100（1-α）%上侧耐受带为:

K1可以查表或由统计软件得到。

考虑占比90%的99%上耐受带。使用（2.28），α =0.01，P =0.90,

以表01的8批药品的纯度数据为例，计算占总体90%的99%上侧耐受区间为：

import numpy as np

from scipy import stats

y1 = [94.20,92.68,94.47,94.14,95.17,94.47,94.14,95.17]

x1 = [1,2,3,4,5,6,7,8]

n1 =len(y1)

ne=n1

x1_mean=np.mean(y1)

sv1=np.var(y1)*n1/(n1-1)

ne=n1

v=n1-1

P=0.90

a=0.01

ncp=stats.norm.ppf(P)*n1**0.5

K1=scipy.special.nctdtrit(v, ncp, 1-a)/n1**0.5

#scipy.special.nctdtrit(df, nc, p)

scipy.special.nctdtrit(v, ncp, 1-a)

L=x1_mean-K1*sv1**0.5

U=x1_mean+K1*sv1**0.5

L

U

>>> L

91.57775463730393

>>> U

97.03224536269609

计算得的耐受区间和预测区间的真实性很大程度取决于数据的正态假设。下面的章节会介绍如保验证这种假设。如果正态假设不成立，可以计算非中心耐受区间。这需要更多的数据。