2.6.10制药CMC统计应用之非正态数据

本文是《Statistical Applications for Chemistry Manufacturing and Controls CMC in the Pharmaceutical Industry》第2章2.6.10节

如前面的例子，除非数据可以很好地用正态模型表示，否则不能使用前面介绍的统计区间的计算公式，特别是预测区间和耐受区间，但是对均值的置信区间影响不大。均值的置信区间对于正态性的假定并不敏感，因为它基于样本均值的抽样分布。中心极限定理能确保抽样分布趋于正态分布个体值服从什么分布。所以对于足够大的数据，等式（2.8）工作得很好，即便不是正态分布。但是如果不是正态分布，预测区间和耐受区间的表现就不好。这些区间的有效性取决于不受中心极限定理影响的个体值。

确定数据是不是正态分布的有用的图是正态分位数图（也称为正态概率图）。图2.9展示了表2.1的纯度值的正态分位数图。水平轴表示测定值，垂直轴表示个体值在数据集中的分位数。垂直轴经过规范化以便数据可以用正态模型描述，测量值将范在直线上以被“胖的铅笔”覆盖。

看起业有理由认为测量值落在图2.9的直线上，所以使用前面的统计量计算区间是合理的。

统计检验可以用来检验正态假设。便是与统计检验相比我们更喜欢用图形表示。统计检验的结果取决于样本量，大的样本通常会得出非正态的结论，小样本通常态少而不能拒绝正态假设。另外，正态假设可以使人们发现从“理想”状态的偏离，猜测可能的数据变换或识别离群值。

当数据不能体现正态模型时，有三种方法进行处理。

1. 确定一种变换使数据拟合正态模型。
2. 用更合适的分布模型化数据。
3. 应用分布自由的或非参数的方法。

第一种方法是确定一种变换以便变换后的数据能通过正态曲线很好的建模。变换后的值T是原测量Y的函数。即使Y没有正态分布，也可以用正态模型表示T。表2.13报告一些常见的变换和条件使Y成功变换。

幂变换，最常见的是Box-Cox变换，是有用的工具。这种变换的形式为

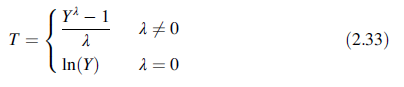
选择λ使变换后的数据符合正态分布。

表2.14 25 μm不溶性微粒的计数

瓶中粒子数    粒数

0              4

1              21

2              11

3               2

用变换后的数据（T）完成分析后，将结果再变回原来值（Y）。例如，如果变换的数据T=ln（Y）用等式（2.23）计算下置信带L，则用原单位报告下置信带为eL。

根据我们的经验，反变换后的预测区间和耐受区间通常太宽而不能使用，当原始数据极度偏斜有及数据量大小时。从实践的角度看，变换数据的策略能于在CMC应用中使用。另外数据分析的客户不喜欢“改变数据”这一事实，即便从统计的角度看分析的结果很好。

作为替代，可以使用更合适的分布来计算统计区间。随着统计软件的发展，这种方法在许多研究者的能力范围内。

用西林瓶内或预充针内的不溶性微粒的例子来说明这种方法。历史上，时间或空间上的计数变量使用泊松分布，这种模型可以很好的体现不溶性微粒的计数。表2.14汇总了38个西林瓶中大于25um的不溶性微粒的计数。例如，38瓶中，有4瓶不存在粒子，有21瓶有1个粒子。用泊松分布计算平均值λ的单侧和双侧耐受区间，基于准确的或规一化的 λ的置信区间。要计算包含100P%总体的双侧100（1-α）%耐受区间，从泊松均值λ的100（1-2α）%置信区间开始，推荐的λ的100（1-2α）%置信区间为

其中n为样本量且m为所有n个值的和。上置信带现在为均值为U的泊松分布的（1+P）/2分位数,下置信带为均值为L的泊松分布的（1-P）/2分位数。

这种计算可以用python的stats.poisson.cdf计算。使用表2.14的数据，n=38且m =0 × 4+ 1 × 21+ 2×11+ 3×2=49。构建包含99.5%的未来值的95%双侧耐受区间，α =0:025 且P=0:995。从（2.34）式计算λ的双侧置信区间。

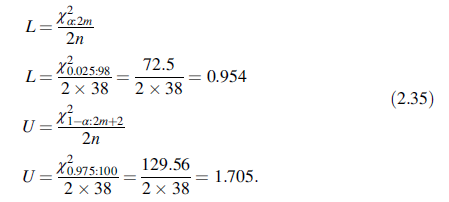
>>> stats.poisson(mu=1.705).cdf(6)

0.9980941068819913

>>> stats.poisson(mu=0.954).cdf(0)

0.38519714916775516

备注：EXCEL 里POISSON(x,mean,cumulative)

X 必需。事件数。Mean 必需。期望值。Cumulative 必需。一逻辑值，确定所返回的概率分布的形式。如果 cumulative 为 TRUE，函数 POISSON 返回泊松累积分布概率，即，随机事件发生的次数在 0 到 x 之间（包含 0 和 1）的概率；如果为 FALSE，则返回泊松概率密度函数，即，随机事件发生的次数恰好为 x 的泊松概率密度函数。

要计算耐受区间的上置信带，stats.poisson.cdf找到最小的整数使概率超过（1+P）/2=0.9975，均值U=1.705。这得到“stats.poisson(mu=1.705).cdf(6)=0.9981”。所以上置信带为6个粒子。下置信带为0因为”stats.poisson(mu=0.954).cdf(0)=0.3852“超过（1-P）/2=0.0025，且下置信带不可能小于零。

直觉上发现如果这些数据用基于正态分布的公式（2.23）计算双侧耐受区间，L =-1.292,及U=3.871。从这个结果可以看出基于正态的上置信带太小因为它没有考虑数据的偏斜。也可以用二项分布。广义线性回归提供更通用的方法来构建不同概率分布模型的统计区间。对于大数据集也可以使用非参数的方法。