二叉树的前驱和后继

最新推荐文章于 2024-10-21 18:32:33 发布

划船不靠桨2022

最新推荐文章于 2024-10-21 18:32:33 发布

阅读量2.8w

点赞数 20

分类专栏： Linux-C++ 文章标签：前驱后继二叉树父子节点

本文链接：https://blog.csdn.net/liuchaoswu/article/details/45456707

版权

本文探讨了二叉树中结点的前驱和后继节点的概念，通过先序、中序和后序遍历的方式详细阐述了如何找到这些节点，并给出了C++实现的讨论及代码测试。

摘要由CSDN通过智能技术生成

前提

二叉树的几何结构和遍历路径，是查找前驱和后继的基础。

结点分类

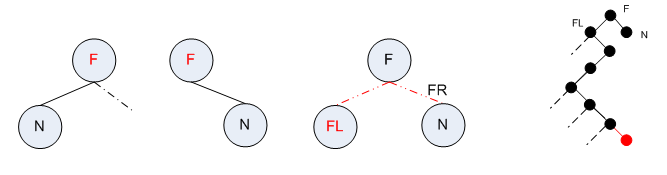
几何结构千变万化，但单个结点必然和至多3点邻接：左（或右）父，左子和右子。按照“X”型助记，交叉点为研究对象。为求结点N的前驱结点Pre和后继结点Suc，设N的左子lchild，右子rchildm，N的左父亲lparent，右父亲rparent；
二叉树的结构

先后顺序

同一几何结构，不同的遍历方式得到不同的遍历路径；具体到单个结点，也就有不同的前驱结点和后继结点。

定义的二叉树数据结构(C++)

template<typename T> struct BNode
{
    T m_data;
    BNode<T>* rchild;
    BNode<T>* lchild;
    BNode<T>* parent;
    int ltag;
    int rtag;
    BNode(T data=0):m_data(data),rchild(NULL),lchild(NULL),parent(NULL),ltag(0),rtag(0){}
};
template<typename T> struct BTree
{
    BNode<T>* m_root;
    BNode<T>* index;
    BNode<T>* pre;
    T m_data;
    BTree(BNode<T>* root=NULL,T data=0):m_root(root),m_data(data),pre(NULL){}
}

具体讨论

4.1 先序遍历
先序前驱与后序后继，先序后继与后续前驱，和中序前驱与中序后继，分别形成3对镜像过程。
4.1.1 先序前驱
这里写图片描述

若当前节点拥有右父亲节点,则Pre=node->parent；

若当前节点拥有左父亲节点,且父亲节点左子树为空，则Pre=node->parent;

若当前节点拥有左父亲节点,且父亲节点左子树不为空,则Pre等于父亲节点左子树的最右的末节点（至右至左）；

T get_pre_pre(BNode<T>* root)//先序遍历的前驱节点
{
    if(root==NULL)
    {
        return 0;
    }
    BNode<T>* father=root->parent;
    if(!father)
    {
        return 0;
    }
    if(root==father->lchild)
    {
        return father->m_data;
    }
    else if(root==father->rchild)
    {
        if(!father->lchild)
        {
            return 0;
        }
        BNode<T>* child=father->lchild;
        while(child->rchild||child->lchild)
        {
            while(child->rchild)
            {