0034算法笔记——【分支限界法】最优装载问题

最新推荐文章于 2021-06-09 14:30:04 发布

风仲达

最新推荐文章于 2021-06-09 14:30:04 发布

阅读量2w

点赞数 13

分类专栏：算法算法笔记——《算法设计与分析》文章标签：最优装载问题分支限界法算法笔记最大堆优先队列式

本文链接：https://blog.csdn.net/liufeng_king/article/details/8910956

版权

本文介绍了如何使用队列式和优先队列式分支限界法解决最优装载问题。通过策略优化，首先尽可能填满第一艘船，再装第二艘。详细探讨了算法流程，包括结点的左子树表示装船，右子树表示不装，以及剪枝条件。同时提供了算法代码实现，包括Queue.h和MaxHeap.h文件。

摘要由CSDN通过智能技术生成

问题描述

有一批共个集装箱要装上2艘载重量分别为C1和C2的轮船，其中集装箱i的重量为Wi，且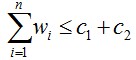装载问题要求确定是否有一个合理的装载方案可将这个集装箱装上这2艘轮船。如果有，找出一种装载方案。

容易证明：如果一个给定装载问题有解，则采用下面的策略可得到最优装载方案。
(1)首先将第一艘轮船尽可能装满；
(2)将剩余的集装箱装上第二艘轮船。

1、队列式分支限界法求解

在算法的循环体中，首先检测当前扩展结点的左儿子结点是否为可行结点。如果是则将其加入到活结点队列中。然后将其右儿子结点加入到活结点队列中(右儿子结点一定是可行结点)。2个儿子结点都产生后，当前扩展结点被舍弃。

活结点队列中的队首元素被取出作为当前扩展结点，由于队列中每一层结点之后都有一个尾部标记-1，故在取队首元素时，活结点队列一定不空。当取出的元素是-1时，再判断当前队列是否为空。如果队列非空，则将尾部标记-1加入活结点队列，算法开始处理下一层的活结点。

节点的左子树表示将此集装箱装上船，右子树表示不将此集装箱装上船。设bestw是当前最优解；ew是当前扩展结点所相应的重量；r是剩余集装箱的重量。则当ew+r<bestw时，可将其右子树剪去，因为此时若要船装最多集装箱，就应该把此箱装上船。另外，为了确保右子树成功剪枝，应该在算法每一次进入左子树的时候更新bestw的值。

为了在算法结束后能方便地构造出与最优值相应的最优解，算法必须存储相应子集树中从活结点到根结点的路径。为此目的，可在每个结点处设置指向其父结点的指针，并设置左、右儿子标志。

找到最优值后，可以根据parent回溯到根节点，找到最优解。

算法具体代码实现如下：

1、Queue.h

#include<iostream>
using namespace std;

template <class T>
class Queue
{
	public:
		Queue(int MaxQueueSize=50);
		~Queue(){delete [] queue;}
		bool IsEmpty()const{return front==rear;}
		bool IsFull(){return ( (  (rear+1)  %MaxSize==front )?1:0);}
		T Top() const;
		T Last() const;
		Queue<T>& Add(const T& x);
		Queue<T>& AddLeft(const T& x);
		Queue<T>& Delete(T &x);
		void Output(ostream& out)const;
		int Length(){return (rear-front);}
	private:
		int front;
		int rear;
		int MaxSize;
		T *queue;
};

template<class T>
Queue<T>::Queue(int MaxQueueSize)
{
	MaxSize=MaxQueueSize+1;
	queue=new T[MaxSize];
	front=rear=0;
}

template<class T >
T Queue<T>::Top()const
{
	if(IsEmpty())
	{
		cout<<"queue:no element,no!"<<endl;
		return 0;
	}
	else return queue[(front+1) % MaxSize];
}

template<class T>
T Queue<T> ::Last()const
{
	if(IsEmpty())
	{
		cout<<"queue:no element"<<