凸包问题

凸包问题的六种解决方案–Graham算法

目录：

• 凸包定义
• 要解决问题
• Graham算法
• 代码块

---

凸包定义

设平面上有一点集S，存在一最小的凸多边形P，使S中的点或在P的边界上或在P的内部，我们称P为S的凸包。

要解决问题

    （poj1113） Wall

Time Limit: 1000MS Memory Limit: 10000K

Description

Once upon a time there was a greedy King who ordered his chief Architect to build a wall around the King’s castle. The King was so greedy, that he would not listen to his Architect’s proposals to build a beautiful brick wall with a perfect shape and nice tall towers. Instead, he ordered to build the wall around the whole castle using the least amount of stone and labor, but demanded that the wall should not come closer to the castle than a certain distance. If the King finds that the Architect has used more resources to build the wall than it was absolutely necessary to satisfy those requirements, then the Architect will loose his head. Moreover, he demanded Architect to introduce at once a plan of the wall listing the exact amount of resources that are needed to build the wall.

Your task is to help poor Architect to save his head, by writing a program that will find the minimum possible length of the wall that he could build around the castle to satisfy King’s requirements.

The task is somewhat simplified by the fact, that the King’s castle has a polygonal shape and is situated on a flat ground. The Architect has already established a Cartesian coordinate system and has precisely measured the coordinates of all castle’s vertices in feet.

Input

The first line of the input file contains two integer numbers N and L separated by a space. N (3 <= N <= 1000) is the number of vertices in the King’s castle, and L (1 <= L <= 1000) is the minimal number of feet that King allows for the wall to come close to the castle.

Next N lines describe coordinates of castle’s vertices in a clockwise order. Each line contains two integer numbers Xi and Yi separated by a space (-10000 <= Xi, Yi <= 10000) that represent the coordinates of ith vertex. All vertices are different and the sides of the castle do not intersect anywhere except for vertices.

Output

Write to the output file the single number that represents the minimal possible length of the wall in feet that could be built around the castle to satisfy King’s requirements. You must present the integer number of feet to the King, because the floating numbers are not invented yet. However, you must round the result in such a way, that it is accurate to 8 inches (1 foot is equal to 12 inches), since the King will not tolerate larger error in the estimates.

Sample Input
9 100
200 400
300 400
300 300
400 300
400 400
500 400
500 200
350 200
200 200

Sample Output
1628

Hint
结果四舍五入就可以了

Graham算法

时间复杂度：nlogn
思想描述：找出给定点集中的一个点，以这个点为起点以逆时针方向开始找凸包上的点。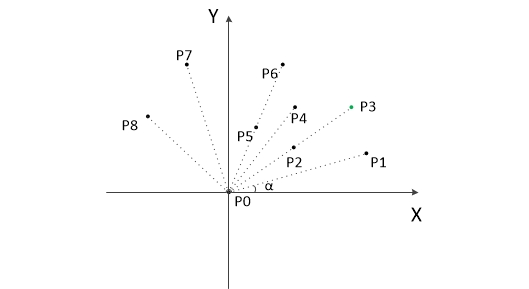
步骤：
准备工作：
1、将给定点集中的点放在笛卡尔坐标系中，找到最下方的点（如果存在多个点的y坐标相同，则取最左边的点）p0。
2、移动坐标系使p0为原点。如上图所示。
3、计算各个点相对于p0的幅角 α ，按从小到大的顺序将各个点排序，如果幅角相同，则距离p0较近的点排在前面。如上图所示，各个点的排列顺序为：p0,p1,p2,p3,p4,p5,p6,p7,p8。

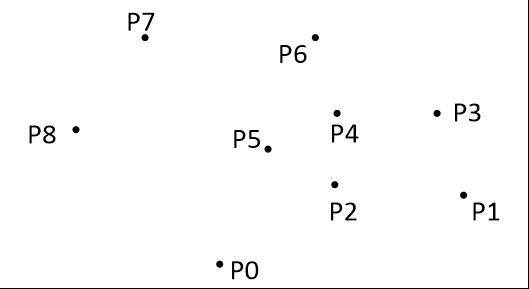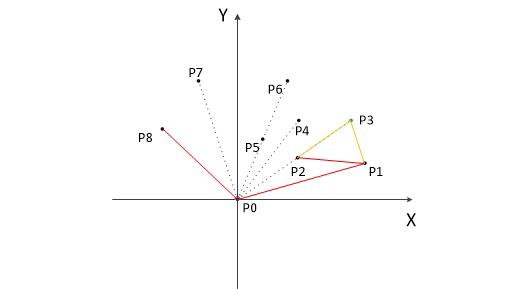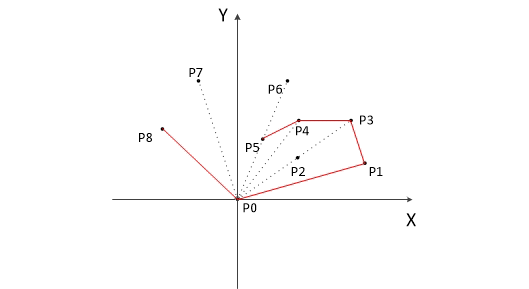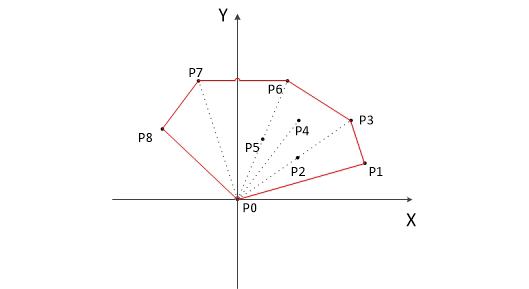
将p0和p1放到栈stack中，并取p1后面的点p2作为当前点。接下来准备找第三个：

4、连接栈stack[top-1]中的点和栈顶的点stack[top]，形成直线L，判断当前点在L的左边还是右边，如果在直线的右边，则执行步骤5；如果在直线的左边，则执行步骤6。
5、如果当前点在直线的右边，则栈顶的点不是凸包上的点，将栈顶的点弹出，执行步骤4。
6、如果当前点在直线的左边，则当前点是凸包上的点，将次点压栈，执行步骤7。
7、判断压入栈的点是否是步骤3中排列后的最后一个点，如果是，结束；如果不是，继续把当前点的后面一个点做为当前点，继续执行步骤4。

最后栈中的元素即为凸包上的所有点。
以下是Graham算法动态求凸包的过程：

代码块

poj1113：

#include<stdio.h>
#include<iostream>
#include<math.h>
#include<algorithm>

const double PI = acos(-1.0);//acos是余弦的反函数，printf("%g",PI)，则PI = 3.14159 
const int maxn = 1000;

using namespace std;

struct Point
{
    int x,y;
};

Point list[maxn];
int stack[maxn],top;

double Dis(Point p0, Point p1)
{
    double dis = sqrt((double)((p0.x - p1.x) * (p0.x - p1.x) + (p0.y - p1.y) * (p0.y - p1.y)));
    return dis;
}

int cross(Point p0, Point p1, Point p2)//计算叉积 
{
    return ( (p1.x - p0.x) * (p2.y - p0.y) - (p1.y - p0.y) * (p2.x - p0.x) );//结果大于0则返回1 
}

bool cmp(Point p0, Point p1)//极角排序，极角相等（向量重合）时按距离从小到大排序 
{
    int temp = cross(list[0],p0,p1);
    if(temp > 0)return true;
    else if(temp == 0 && (Dis(list[0], p0) < Dis(list[0], p1)))return true;
    else return false;
}

void init(int n)
{
    int i, k;
    Point p0;
    scanf("%d %d",&list[0].x, &list[0].y);
    p0.x = list[0].x;
    p0.y = list[0].y;
    k = 0;
    找出最下最左方点赋值给list[0] 
    for(i = 1; i < n; i++)
    {
        scanf("%d %d",&list[i].x, &list[i].y);
        if(p0.y > list[i].y || ((p0.y == list[i].y) && (p0.x > list[i].x)) )
        {
            p0.x = list[i].x;
            p0.y = list[i].y;
            k = i; 
        }
    }
    list[k] = list[0];
    list[0] = p0;

    sort(list+1, list+n, cmp);

}

void GraHam(int n)
{
    int i;
    if(n == 1)
    {
        top = 0;
        stack[0] = 0;
    }
    if(n == 2)
    {
        top = 1;
        stack[0] = 0;
        stack[1] = 1;
    }
    if(n > 2)
    {
        for(i = 0; i <= 1; i++)stack[i] = i;
        top = 1;

        for(i = 2; i < n; i++)
        {
            while(top > 0 && cross(list[stack[top-1]],list[stack[top]],list[i]) <= 0) top--;
            top++;
            stack[top] = i;
        }
    }
}

int main()
{
    int N,L;
    while(scanf("%d %d",&N, &L) != EOF)
    {
        init(N);
        GraHam(N);
        double res = 0;
        for(int i = 0; i < top; i++)
            {
                res += Dis(list[stack[i]],list[stack[i+1]]);
                //printf("%d ",(int)(res));
            }
        res += Dis(list[stack[0]],list[stack[top]]);
        //printf("%d ",(int)(res));
        res += 2 * PI * L;
        printf("%d\n",(int)(res+0.5));
    }
    return 0;
}

脚注

参考链接http://blog.csdn.net/bone_ace/article/details/46239187.