蓝桥杯 ADV-298 算法提高和谐宿舍2

最新推荐文章于 2022-04-06 09:47:47 发布

liulizhi1996

最新推荐文章于 2022-04-06 09:47:47 发布

阅读量1.6k

点赞数 3

CC 4.0 BY-SA版权

分类专栏：蓝桥杯

本文链接：https://blog.csdn.net/liulizhi1996/article/details/104223810

蓝桥杯专栏收录该内容

232 篇文章

订阅专栏

本文探讨了在有限资源下，如何通过算法优化来解决宿舍作品覆盖问题，旨在找到使用最少面积的木板覆盖所有作品的方法，介绍了动态规划的递推关系及其实现过程。

算法提高和谐宿舍2

时间限制：1.0s 内存限制：256.0MB

问题描述

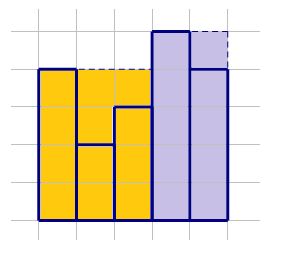
　　我的某室友学过素描，墙上有n张他的作品。这些作品都是宽度为1，高度不定的矩形，从左到右排成一排，且底边在同一水平线上。
　　宿舍评比就要来了，为了及格，我们决定买不多于m块的矩形木板，把这些作品和谐掉。要求木板也从左到右排成一排，且底边与作品的底边在同一水平线上。
　　在能够把所有作品和谐掉的前提下，我们希望这些木板的面积和最小，问最小面积和。

输入格式

　　第一行两个数n和m，表示作品数和木板数；
　　第二行n个数Hi，表示从左到右第i个作品的高度。

输出格式

　　一行一个数ans，表示答案。

样例输入

5 2
4 2 3 5 4

样例输出

数据规模和约定

　　对于30%的数据：1<=n，m<=10；
　　对于100%的数据：1<=n，m<=100，1<=Hi<=10000。

分析：记这些作品依次为 $a_1, a_2, \cdots, a_n$ ，记 $MAX[i][j]$ 为 $a_i, a_{i+1}, \cdots, a_{j-1}, a_{j}$ 中的最大值。设 $f(i, j)$ 为使用 $j$ 块木板覆盖第1至第 $i$ 件作品的最小面积和。递推关系式为

$f(i, j) = \min_{k=1 .. i-j+1} \{ f(i-k, j-1) + k \cdot MAX[i-k+1][i] \}, j \le \min\{i, m\}$ $(j \ge 2)$

初始条件： $f(i, 1) = i \cdot MAX[1][i]$

#include <stdio.h>

#define INF 0x3F3F3F3F

int max(int a, int b)
{
    return a > b ? a : b;
}

int min(int a, int b)
{
    return a < b ? a : b;
}

int main()
{
    int n, m;
    int heights[105] = { 0 };
    int max_height[105][105] = { 0 };
    int f[105][105] = { 0 };

    scanf("%d %d", &n, &m);
    for (int i = 1; i <= n; ++i)
        scanf("%d", &heights[i]);

    for (int i = 1; i <= n; ++i)
    {
        max_height[i][i] = heights[i];
        for (int j = i + 1; j <= n; ++j)
            max_height[i][j] = max(max_height[i][j-1], heights[j]);
    }

    for (int i = 1; i <= n; ++i)
    {
        f[i][1] = i * max_height[1][i];
        for (int j = 2; j <= i && j <= m; ++j)
        {
            f[i][j] = INF;
            for (int k = 1; k <= i-j+1; ++k)
                f[i][j] = min(f[i][j], f[i-k][j-1] + k * max_height[i-k+1][i]);
        }
    }
    printf("%d", f[n][m]);

    return 0;
}