T-tree原理与实现

T-tree

In computer science a T-tree is a type of binary tree data structure that is used by main-memory databases, such as Datablitz, eXtremeDB, MySQL Cluster, Oracle TimesTen and KairosMobileLite.

A T-tree is a balanced index tree data structure optimized for cases where both the index and the actual data are fully kept in memory, just as a B-tree is an index structure optimized for storage on block oriented secondary storage devices like hard disks. T-trees seek to gain the performance benefits of in-memory tree structures such as AVL trees while avoiding the large storage space overhead which is common to them.

T-trees do not keep copies of the indexed data fields within the index tree nodes themselves. Instead, they take advantage of the fact that the actual data is always in main memory together with the index so that they just contain pointers to the actual data fields.

The 'T' in T-tree refers to the shape of the node data structures in the original paper that first described this type of index.^[1]

[edit] Performance

Although T-trees seem to be widely used for main-memory databases, recent research indicates that they actually do not perform better than B-trees on modern hardware:

Rao, Jun; Kenneth A. Ross (1999). "Cache conscious indexing for decision-support in main memory". Proceedings of the 25th International Conference on Very Large Databases (VLDB 1999). Morgan Kaufmann. pp. 78–89. http://www.vldb.org/dblp/db/conf/vldb/RaoR99.html. 

Kim, Kyungwha; Junho Shim, and Ig-hoon Lee (2007). "Cache conscious trees: How do they perform on contemporary commodity microprocessors?". Proceedings of the 5th International Conference on Computational Science and Its Applications (ICCSA 2007). Springer. pp. 189–200. doi:10.1007/978-3-540-74472-6_15. 

The main reason seems to be that the traditional assumption of memory references having uniform cost is no longer valid given the current speed gap between cache access and main memory access.

[edit] Node structures

A T-tree node usually consists of pointers to the parent node, the left and right child node, an ordered array of data pointers and some extra control data. Nodes with two subtrees are called internal nodes, nodes without subtrees are called leaf nodes and nodes with only one subtree are named half-leaf nodes. A node is called the bounding node for a value if the value is between the node's current minimum and maximum value, inclusively.

Bound values.

For each internal node leaf or half leaf nodes exist that contain the predecessor of its smallest data value (called the greatest lower bound) and one that contains the successor of its largest data value (called the least upper bound). Leaf and half-leaf nodes can contain any number of data elements from one to the maximum size of the data array. Internal nodes keep their occupancy between predefined minimum and maximum numbers of elements

[edit] Algorithms

This section requires expansion.

[edit] Search

• Search starts at the root node
• If the current node is the bounding node for the search value then search its data array. Search fails if the value is not found in the data array.
• If the search value is less than the minimum value of the current node then continue search in its left subtree. Search fails if there is no left subtree.
• If the search value is greater than the maximum value of the current node then continue search in its right subtree. Search failes if there is no right subtree.

[edit] Insertion

• Search for a bounding node for the new value. If such a node exist then
  • check whether there is still space in its data array, if so then insert the new value and finish
  • if no space is available then remove the minimum value from the node's data array and insert the new value. Now proceed to the node holding the greatest lower bound for the node that the new value was inserted to. If the removed minimum value still fits in there then add it as the new maximum value of the node, else create a new right subnode for this node.
• If no bounding node was found then insert the value into the last node searched if it still fits into it. In this case the new value will either become the new minimum or maximum value. If the value doesn't fit anymore then create a new left or right subtree.

If a new node was added then the tree might need to be rebalanced, as described below.

[edit] Deletion

• Search for bounding node of the value to be deleted. If no bounding node is found then finish.
• If the bounding node does not contain the value then finish.
• delete the value from the node's data array

Now we have to distinguish by node type:

• Internal node:

If the node's data array now has less than the minimum number of elements then move the greatest lower bound value of this node to its data value. Proceed with one of the following two steps for the half leaf or leaf node the value was removed from.

• Leaf node:

If this was the only element in the data array then delete the node. Rebalance the tree if needed.

• Half leaf node:

If the node's data array can be merged with its leaf's data array without overflow then do so and remove the leaf node. Rebalance the tree if needed.

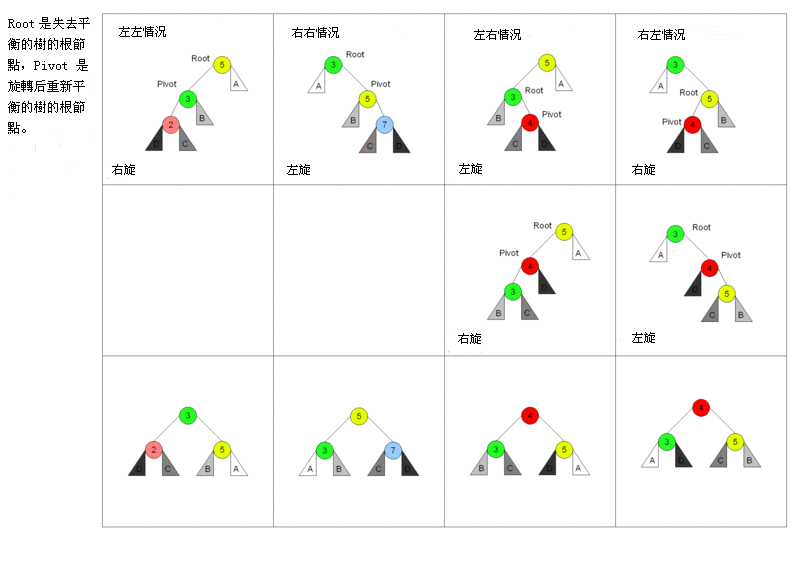
[edit] Rotation and balancing

This section requires expansion.

A T-tree is implemented on top of an underlying self-balancing binary search tree. Specifically, Lehman and Carey's article describes a T-tree balanced like an AVL tree: it becomes out of balance when a node's child trees differ in height by at least two levels. This can happen after an insertion or deletion of a node. After an insertion or deletion, the tree is scanned from the leaf to the root. If an imbalance is found, one tree rotation or pair of rotations is performed, which is guaranteed to balance the whole tree.

When the rotation results in an internal node having fewer than the minimum number of items, items from the node's new child(ren) are moved into the internal node.

  

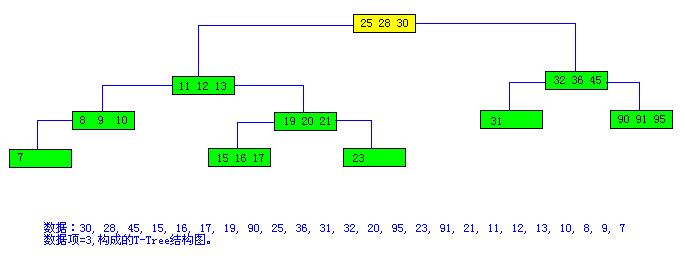
典型T-Tree图