对于C(n, m) mod p。这里的n,m,p(p为素数)都很大的情况。就不能再用C(n, m) = C(n - 1,m) + C(n - 1, m - 1)的公式递推了。
这里用到Lusac定理
A、B是非负整数。
AB写成p进制:
A=a[n]a[n-1]...a[0],B=b[n]b[n-1]...b[0]。
则组合数C(A,B)与C(a[n],b[n])*C(a[n-1],b[n-1])*...*C(a[0],b[0]) mod p同余
即:Lucas(n,m,p)=c(n%p,m%p)*Lucas(n/p,m/p,p)
For non-negative integers m and n and a prime p, the following congruence relation holds:
where
and
are the base p expansions of m and n respectively.
对于单独的C(ni, mi) mod p,已知C(n, m) mod p = n!/(m!(n - m)!) mod p。显然除法取模,这里要用到m!(n-m)!的逆元。
根据费马小定理:
已知(a, p) = 1,则 ap-1 ≡ 1 (mod p), 所以 a*ap-2 ≡ 1 (mod p)。
也就是 (m!(n-m)!)关于p的逆元为 (m!(n-m)!)p-2 ;
定义:
满足a*k≡1 (mod p)的k值就是a关于p的乘法逆元。
为什么要有乘法逆元呢?
当我们要求(a/b) mod p的值,且a很大,无法直接求得a/b的值时,我们就要用到乘法逆元。
我们可以通过求b关于p的乘法逆元k,将a乘上k再模p,即(a*k) mod p。其结果与(a/b) mod p等价。
证:(其实很简单。。。)
根据b*k≡1 (mod p)有b*k=p*x+1。
k=(p*x+1)/b。
把k代入(a*k) mod p,得:
(a*(p*x+1)/b) mod p
=((a*p*x)/b+a/b) mod p
=[((a*p*x)/b) mod p +(a/b)] mod p
=[(p*(a*x)/b) mod p +(a/b)] mod p
//p*[(a*x)/b] mod p=0
所以原式等于:(a/b) mod p
将不大于m颗种子存放在n颗树中,问有多少种存法。
首先是不大于m颗种子,我没可以认为少于m的那些种子存放在了第n+1颗树上,这样的话,问题就转化成了将m颗种子存放在n+1颗树上的方案数。ok这个是组合数学里面的公式,亦即插板法,也就是X1+X2+X3+……+Xn+1 = m;ok,答案是C(n+m,m);
然后就是上面说的Lucas定理解决大组合数问题了
1 <= n, m <= 1000000000, 1 < p < 100000
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
typedef long long LL;
using namespace std;
LL exp_mod(LL a, LL b, LL p) { //快速幂
LL res = 1;
while(b != 0) {
if(b&1) res = (res * a) % p;
a = (a*a) % p;
b >>= 1;
}
return res;
}
LL Comb(LL a, LL b, LL p) {
if(a < b) return 0;
if(a == b) return 1;
if(b > a - b) b = a - b;
LL ans = 1, ca = 1, cb = 1;
for(LL i = 0; i < b; ++i) {
ca = (ca * (a - i))%p;
cb = (cb * (b - i))%p;
}
ans = (ca*exp_mod(cb, p - 2, p)) % p; //乘法逆元的应用
return ans;
}
LL Lucas(int n, int m, int p) {
LL ans = 1;
while(n&&m&&ans) {
ans = (ans*Comb(n%p, m%p, p)) % p; //Lucas的应用
n /= p;
m /= p;
}
return ans;
}
int main() {
LL n, m, p;
int t;
scanf("%d",&t);
while(t--) {
scanf("%lld%lld%lld", &n, &m, &p);
printf("%lld\n", Lucas(n+m, m, p));
}
return 0;
}









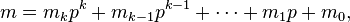
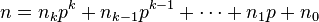














 577
577











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








