Cantor展开、全排列问题、魔板问题（JAVA实现）

Cantor展开、全排列问题、魔板问题（JAVA实现）

本文由全排列问题的递归和非递归写法入手，引出Cantor展开的公式及其应用，最后讨论Cantor数的经典应用之魔板问题

• 全排列问题
• Cantor展开
• 魔板问题

---

目录

问题：给定字符串S[0…N-1]，设计算法，枚举S的全排列

以一个简单的示例来表示解题过程
示例 枚举0123的全排列
0123 0132 0213 0231 0312 0321
1023 1032 1203 1230 1302 1320
2013 2031 2103 2130 2301 2310
3012 3021 3102 3120 3201 3210
手动写出这些序列的时候，实际上是脑补了一个树形结构，如下：

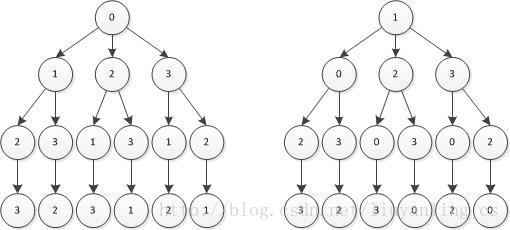
画出这个树的过程实际上是一个深度搜索的过程，每次到达叶子节点时就产生一个输出，之后再回溯，搜索下一个叶子节点。
深度搜索的过程实际上就是一个入栈出栈的过程，也就是一个递归过程。

全排列之递归解法

使用递归时，代码结构是很清晰，也容易理解，便不再赘述，直接上代码。

//无重复的全排列递归写法
public class Permutation {
    public static final int N = 4;
    public static void main(String[] args){
        //初始化
        int[] sequence = new int[N];
        for(int i = 0;i < N;i++){
            sequence[i] = i+1;
        }
        permutation(sequence,N,0);
    }

    private static void print(int[] sequence){
        for(int i : sequence){
            System.out.print(i);
        }
        System.out.println();
    }

    private static void swap(int[] sequence,int i, int j){
        int tmp = sequence[i];
        sequence[i] = sequence[j];
        sequence[j] = tmp;
    }
    //固定前n位的全排列
    public static void permutation(int[] sequence, int size, int n){
        if(n == size - 1) print(sequence);

        for(int i = n; i < size;i++){
            //用其他位来交换第n位
            swap(sequence,i,n);
            permutation(sequence,size,n+1);
            swap(sequence,i,n);
        }
    }
}

当出现重复元素时，在用其他位交换第n位时，会有相同的两个位均与n位发生了交换。所以我们需要在交换时判断该位是否在之前已经被放置到n位过。
为了判断某个元素是否已经被访问过，另增加一个duplication数组。
与无重复元素的序列全排列相比，仅在permutation函数中增加了一个参数及两行代码。
代码如下

//有重复的递归写法
public class PermutationWithDuplicate {
   
    public static final int N = 4;

    public static void main(String[] args){
        //初始化
        int[] sequence = {
  1,2,3,4};
        boolean[] duplication = new boolean[N];
        permutation(duplication,sequence,N,0);
    }

    private