AOV网和拓扑序列

AOV网

AOV网可以用 DAG图（有向无环图） 来表示，AOV网常常用于表示完成一项工作的顺序，如：

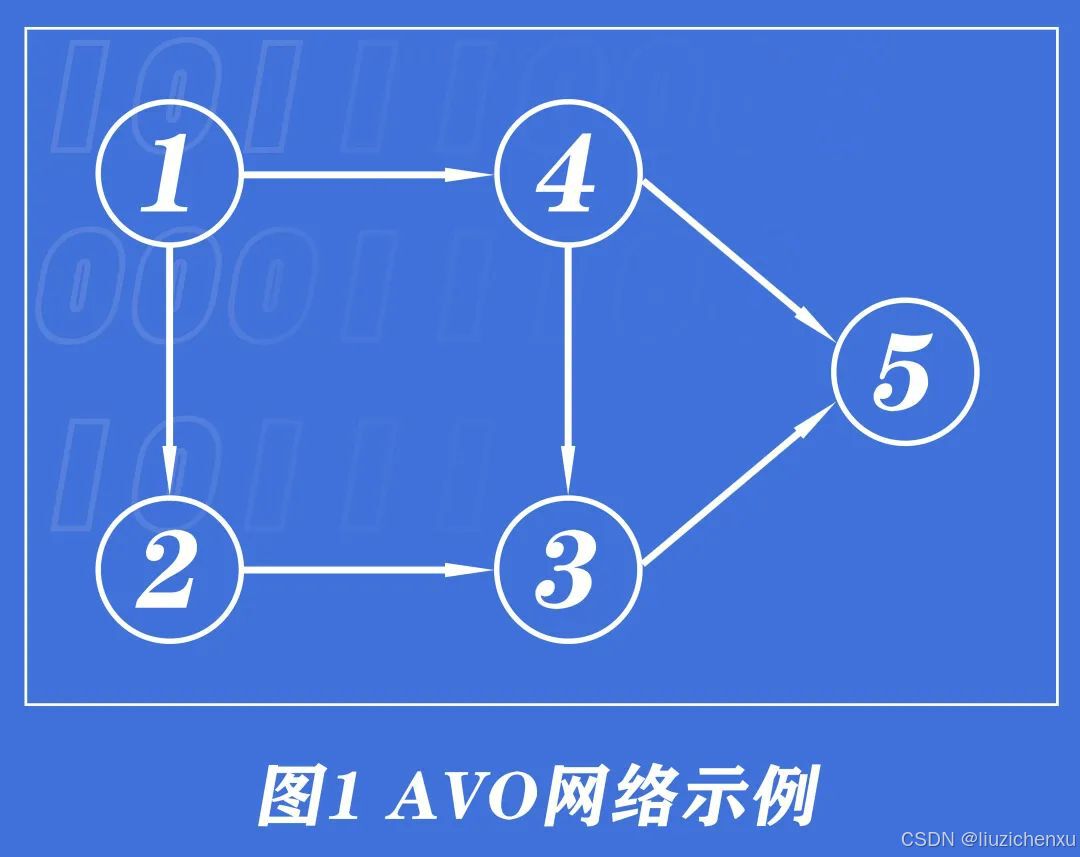
在这里有5个事情要做，分别用1-5来表示，在做2之前，必须先做1。
在AOV网里没有环，比如在做1之前要做2，在做2之前要做3，在做3之前又要先做1，这种情况是不会存在的。
那我们该如何判断AOV网是否合法呢，我们可以用dfs（深度优先搜索）去判断。我们先从入度为0的点开始搜索，当我们搜索到一个已经标记的点时再看一下是不是在同一次搜索当中，如：
先从1开始搜，然后搜到2，在搜到4、5、6，再搜的时候发现又搜到了4，这就是一个不合法的AOV网。
代码如下：

	bool dfs(int x){
 		vis[x]=1;
    	for(auto i:e[x]){
        	if(vis[i]==1) return fales;
        	if(!dfs(i)) return fales;
    	}
    	vis[x]=0;
    	return ture;
	}

在这里还要提到一个知识点，就是前驱和后继，一个点可以有很多前驱或很多后继，如图一 AVO网络试图：1、2、4都是3的前驱，但是2、4是3的直接前驱。1的后继有4、5、3、2，但是只有2和4是1的直接后继。
那我们怎样能遍历一个网呢，这就要用到拓扑排序。

拓扑排序

拓扑排序需要满足以下两个条件：
1、每个顶点出现且只出现一次；
2、若A在序列中排在B的前面，则在图中不存在从B到A的路径。
最经典的例子就是先修课例子了。

拓扑有序序列不唯一，给出一个答案：
C1 → C3 → C2 → C4 → C6 → C5 → C7
那我们如何用代码实现呢，我们可以先把所有点的入度用数组记录一下，再用vector（动态数组）存一下谁是谁的直接前驱，在建立一个queue（队列）把入度为0的点入队，在队列不为空的前提下，先用一个变量存一下队首，出队首，输出，一个个遍历队首的直接后继，并且把他们的入度减一，再入队。最终就可以遍历并输出。
代码如下：

#include<bits/stdc++.h>
using namespace std;
int n,m,x,y,ans[101],cnt;
int a[105]={0},out[105];
vector<int> v[105];
queue<int> q;
int main(){
    cin>>n>>m;
    for(int i=1;i<=m;i++){
        cin>>x>>y;
        a[y]++;
        out[x]++;
        v[x].push_back(y);
    }
    for(int i=1;i<=n;i++){
        if(a[i]==0){
           q.push(i);
        }
    }
    while(!q.empty()){
        int x=q.top();
        q.pop(); 
        cout<<x<<" ";
        for(auto i:v[x]){
            if(--a[i]==0){
                q.push(i);
            }
        }
    }
    return 0;
}

如果让用字典序最大或最小来输出就可以用小顶堆或大顶堆，时间复杂度为O(n*log[n])。