面试官夺命三连
KMP 是啥?KMP 能干啥?手写 KMP ?

在计算机科学中,Knuth-Morris-Pratt字符串查找算法(简称为KMP算法)可在一个主文本字符串S内查找一个词W的出现位置。此算法通过运用对这个词在不匹配时本身就包含足够的信息来确定下一个匹配将在哪里开始的发现,从而避免重新检查先前匹配的字符。
这个算法是由高德纳(Donald Ervin Knuth)和沃恩·普拉特在1974年构思,同年詹姆斯·H·莫里斯也独立地设计出该算法,最终由三人于1977年联合发表。
上面这段内容摘自wikipedia,大概就说明了 KMP 这个算法的作用,就是查找一个字符串中某个模式串的出现位置,并且采用的是一种高效的查找方式,这种查找方式通过借助之前已经部分匹配的有效信息来提高匹配的效率。
一、暴力匹配算法
那么 KMP 是怎么具有很高的匹配效率的呢?
首先我们先来看一下暴力匹配算法,然后再去讲解 KMP 是怎么做的,从而对比出 KMP 算法的优势。
现在我们要在字符串S中查找模式串P的位置(为了方便阅读,我把每个字符用空格隔开了,但是实际字符串中并无空格,实际字符串中有空格的地方使用’_’表示,对照下标大家应该可以看得懂)

说明:指针 i 指向字符串S中当前匹配的位置,指针 j 指向模式串P中当前匹配的位置
1.
一开始,i 和 j 都指向数组下标为 0 的位置,也就是从 S[0] 和 P[0] 开始匹配,目前S[0] = ‘L’,S[0] = ‘A’,即 S[0] != P[0] ,当前字符失配。

那么此时我们令 “ i = i - (j - 1), j = 0 ”,也就是让 i 回溯,且 j 重置为0,这就相当于将模式串P向后移动了一位。
2.
移动之后,发现 S[1] 和 P[0] 还是失配,那么我们继续令 “ i = i - (j - 1), j = 0 ”,此时 i = 2,j = 0。

3.
模式串P继续向后移动,直到匹配到 i = 4,此时 S[4] = P[0],匹配成功,令 “ i++, j++ ”,继续向后匹配

4.
当 i = 10,j = 6 时,S[10] = ’ ‘, p[6] = ‘D’,S[10] != P[6],此时失配,令 “ i = i - (j - 1), j = 0 ”,此时 i = 5,j = 0

5.
这个时候,i 指针又回溯到了 5 这个位置,然后重新进行比较

而这就是该算法低效的主要原因,因为之前在比较的时候已经判断过,我们知道 S[4] = P[0],S[5] = P[1],且 P[0] != P[1],所以 P[0] 肯定和 S[5] 不相等,这样继续比较 P[0] 和 S[5] 是重复的。
而 KMP 算法的高效就在于对这种情况的优化,因为在之前已经积累了足够的信息,它 利用之前部分匹配的有效信息来修改指针 j 的位置,从而使得指针 i 不需要再进行回溯,那么这个问题就变成了在每个位置计算模式串的最长前缀后缀,其实就是一个动态规划问题。
接下来,我们来看看 KMP 是怎么做到的。
二、KMP算法
我们还是从上面那个例子继续说

如图,当我们匹配到 S[10] 和 P[6] 时,此时失配,KMP 算法并不会像暴力匹配那样,将模式串P向右移动一位,然后继续比较。它采用的方式是,如果发生失配,则 i 不变,令 j = next[j](先知道 next[6] = 2,后面我再解释 next[] 数组是怎么得来的),那么此时模式串P相当于向右移动了 4 个位置。

为什么要这样移动呢?因为在 P[2] 前面的 ” AB ” 又可以和 S[10] 前面的 ” AB ” 匹配上,从这里继续向后比较是有可能匹配成功的,并且我们没有重复的去比较不可能匹配成功的前几个字符,从而能提高模式串P移动的速率,即提高的算法的效率。
到这里,就可以看出来 KMP 算法的核心就在于那个 next[] 数组,接下来我们来看看这个 next[] 数组到底是怎么得来的。
三、对于 next[] 数组的理解
这个 next[] 数组,其实和一个 最大长度表密切相关,我们先来看怎样得到这个表。
首先,我们先清楚一个概念,最长前缀后缀
前缀,指的就是除去末尾元素,该字符串的所有头部组合的集合;
后缀,指的就是除去头部元素,该字符串的所有尾部组合的集合;
那么,最长前缀后缀,指的就是前缀与后缀这两个集合中,公共元素的最大长度。
举个栗子:“ AABA ” 这个字符串的前缀就是 [A, AA, AAB] ,后缀是 [ABA, BA, A],则公共元素只有 ” A “,则最长前缀后缀为 1 。
明白最长前缀后缀之后,我们便可以计算得出最大长度表了,下面就是得到字符串 “ ABCDABD ” 的最大长度表的过程:
- " A " 的前缀和后缀都为空集,则该字符串的最长前缀后缀为 0 ,因为没有公共元素;
- " AB " 的前缀为 [A] ,后缀为 [B] ,则该字符串的最长前缀后缀为 0 ,因为没有公共元素;
- " ABC " 的前缀为 [A, AB] ,后缀为 [BC, C] ,则该字符串的最长前缀后缀为 0 ,因为没有公共元素;
- " ABCD " 的前缀为 [A, AB, ABC] ,后缀为 [BCD, CD, D] ,则该字符串的最长前缀后缀为 0 ,因为没有公共元素;
- " ABCDA " 的前缀为 [A, AB, ABC, ABCD] ,后缀为 [BCDA, CDA, DA, A] ,共有元素为 " A " ,则该字符串的最长前缀后缀为 1;
- " ABCDAB " 的前缀为 [A, AB, ABC, ABCD, ABCDA] ,后缀为 [BCDAB, CDAB, DAB, AB, B] ,共有元素为 " AB " ,则该字符串的最长前缀后缀为 2;
- " ABCDABD " 的前缀为 [A, AB, ABC, ABCD, ABCDA, ABCDAB] ,后缀为 [BCDABD, CDABD, DABD, ABD, BD, D] ,则该字符串的最长前缀后缀为 0 ,因为没有公共元素。、根据以上计算得到字符串 ” ABCDABD ” 的每个子串的 最长前缀后缀,可以得到这样一个 最大长度表

这个表就是:模式串子串对应的各个前缀后缀的公共元素的最大长度表
因为模式串中首尾可能会有重复的字符,所以得到如下结论:
遇到失配时,模式串向右移动的位数为:
已匹配字符数 - 失配字符的上一位字符所对应的最大长度值 ,如果已匹配字符数为0,则直接向右移动一位
下面,我们来看一下具体是怎么匹配的:
还是以这两个字符串为例
1.
一开始字符是不匹配的,直接将模式串P右移即可。

2.
直到找到第一个匹配成功的字符,然后继续向后比较

3.
当比较到 i = 10,j = 6 ,发现失配,令 j = next[j],其中,next[j] = 2,根据前面得到的结论:模式串向右移动的位数为 已匹配字符数 - 失配字符的上一位字符所对应的最大长度值 ,那么,此时模式串移动的位数就是:6 - 2,即向右移动 4 位。

4.
移动后,继续比较,此时 i = 10,j = 2,发现失配,那么根据结论,模式串向右移动的位数是: 2 - 0 ,即向右移动 2 位

5.
此时仍然失配,且已匹配的字符数为 0 ,则向右移动一位

6.
右移一位后匹配成功,i ,j 指针继续向后走,直到 i = 17,j = 6,此时失配,那么应该向右移动:6 - 2 位,即右移 4 位。

7.
右移 4 位之后,匹配成功,最终找到了模式串P在字符串S中的位置。

这个过程走下来,可以看出关键就是找到每个失配字符前面的字符的最长前缀后缀,根据这个来移动模式串,而 next[] 数组就是最大长度表的体现。
在使用最大长度表进行匹配时,可以观察到,其实我们没有必要去考虑当前失配的字符,只需要当前失配字符的前一个字符就可以,因此,next[] 数组和最大长度表的区别就是,整个 next[] 数组将最大长度表中的值向后移了一位,并且第一个值置为 -1,即在 next[] 数组中每个字符对应的值其实是它前一个字符在最大长度表中对应的值。

四、递推计算 next[] 数组
我们已经比较感性的去理解了 next[] 数组存放的值是通过计算子串的最长前缀后缀得来的,那么在代码中,具体是怎么计算的呢?
首先,我们在计算 next[j] 的时候,需要分类讨论一下
1.
j = 0 时,next[j] = -1。这个很好理解,因为 j = 0 时,肯定不能再向前移动了。
2.
j = 1 时,next[j] = 0。因为此时 j 只能移动到 0 ,所以 next[j] = 0。
3.
前面两种属于特殊一点的情况,接下来就要考虑普遍的情况了。
对于k,已知P[0 ~ k-1] = P[j-k ~ j-1]。意思就是next[j] = k。
那么接下来我们就需要计算 next[j + 1] 才能完成递推
当 P[k] = P[j] 时,则 next[j + 1] = next[j] + 1 = k + 1。这种情况的证明如下,这个证明很直白,大家不要一看到证明就头疼~
已知 next[j] = k ,且 P[k] = P[j],则 P[0 ~ k-1] + P[k] = p[j-k ~ j-1] + P[j]。
即:P[0 ~ k] = P[j-k ~ j],即next[j + 1] = k + 1 = next[j] + 1。
4.
比较难理解的是 P[k] != P[j] 这种情况
从图里可以看到,此时 P[k] != P[j]

看上面这个图,此时 P[j + 1] 指向的字符是 ‘E’ ,并且 k = 2,那么我们可以看出来 ‘E’ 前面的模式串的最长前缀后缀是 2 ,即 ” AB ” ,很明显,此时是对于 ‘E’ 前面的模式串是不存在最长前缀后缀为 k + 1 = 3,也就是 ” ABC ” 这种情况的,所以我们只能缩小这个范围,去找是不是有长度更短的公共前缀后缀。
在代码中的对这种情况的处理就是令 k = next[k] ,那么为什么要不断递归 k = next[k] 就能找到更短的公共前缀后缀呢?

上图中这个模式串,现在把它变成下面图中的样子

我们现在是将 ” ABAC ” 这一段字符串(也就是 k 及其之前的字符串)拿出来,这样方便肉眼比较。
现在我们拿前缀 ” ABAC ” 去跟后缀 ” ABAB ” 匹配,如果 P[k] != P[j],下一步就是用p[next[k]] 去跟 P[j] 继续匹配,然后重复这个过程,因为这个时候我们是肯定找不到 ” ABAB ” 这个最长的后缀串了,但是我们可以尝试得到更短的,那么这个递归,其实就相当于在图中上面的字符串 ” DABABC ” 中查找 ” ABAC ” 位置的过程!最后得到的就是更短的公共前缀后缀 or 没有最短的公共前缀后缀。
终于,我们可以写出第一份 KMP 代码了
public static int kmp(String string, String pattern) {
char[] s = string.toCharArray();
char[] p = pattern.toCharArray();
int len_s = string.length;
int len_p = pattern.length;
int i = 0, j = 0;
int[] next = getNext(pattern);
while (i < len_s && j < len_p) {
if (j == -1 || s[i] == p[j]) {
i++;
j++;
} else {
j = next[j];
}
}
if (j == p.length) {
return i - j;
} else {
return -1;
}
}
public static int[] getNext(String pattern) {
char[] p = pattern.toCharArray();
int[] next = new int[p.length];
next[0] = -1;
int j = 0;
int k = -1;
while (j < p.length - 1) {
if (k == -1 || p[j] == p[k]) {
j++;
k++;
next[j] = k;
} else {
k = next[k];
}
}
return next;
}但是,这份代码还是存在一个问题的。
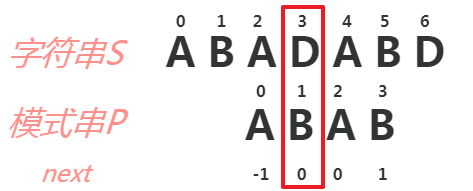
我们来看,现在对这个模式串 ” ABAB ” 进行查找,可以得出这个模式串的 next[] 数组值为 [-1, 0, 0, 1]

在当前位置发生失配,计算后该模式串应向右移动 3 - 1 = 2 位。
 g
g
移动之后,我们发现在这个位置又发生了失配,需要再次计算并移动。
但是,其实在上一步,已经可以得到 P[3] = ‘B’,S[3] = ‘C’,且 P[3] != S[3],而 P[next[3]],即 P[1] = ‘B’ = P[3] 这些信息,所以可以判断得出 P[1] != S[3],但是根据之前的算法,我们还是需要再次判断,并没有利用到之前的有效信息,这是我们所不希望的。
那么,为什么会出现这样的问题呢?
这是因为,我们举例的这个模式串 ” ABAB “,是我们之前没有考虑到的一种模式串情况,这种情况就是 P[j] = P[next[j]] 的情况。
因为当发生失配后,根据算法,一定会继续移动模式串,然后继续比较 P[next[j]] 与 S[j],又因为 P[j] = P[next[j]] 且 P[j] != S[j],所以必然 P[next[j]] != S[j]。
因此,为了解决这个问题,我们应对算法进行一些改进,在出现 P[j] = P[next[j]] 这种情况时,需要继续递归,让 k = next[k] = next[next[k]];
改进后的代码:
public static int[] getNext(String pattern) {
char[] p = pattern.toCharArray();
int[] next = new int[p.length];
next[0] = -1;
int j = 0;
int k = -1;
while (j < p.length - 1) {
if (k == -1 || p[j] == p[k]) {
j++;
k++;
if (p[j] != p[k]) {
next[j] = k;
} else {
next[j] = next[k];
}
} else {
k = next[k];
}
}
return next;
}参考资料:
《算法导论》 字符串匹配
https://blog.csdn.net/v_july_v/article/details/7041827
http://www.ruanyifeng.com/blog/2013/05/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm.html
https://kirainmoe.com/blog/post/kmp-algorithm-for-matching-string/






















 2154
2154

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








