数据挖掘与机器学习入门

导论：

机器学习算法最适用的场景就是：不便用规则处理的场合

数据挖掘（Data Mining）：是有组织有目的地收集数据，通过分析数据使之成为信息，从而在大量数据中寻找潜在规律以形成规则或知识的技术。

机器学习(Machine Learning, ML)：是一门多领域交叉学科，涉及概率论、统计学、逼近论、凸分析、算法复杂度理论等多门学科。专门研究计算机怎样模拟或实现人类的学习行为，以获取新的知识或技能，重新组织已有的知识结构使之不断改善自身的性能。它是人工智能的核心，是使计算机具有智能的根本途径，其应用遍及人工智能的各个领域。目前，世界上共有几百种不同的机器学习算法。

数据挖掘与机器学习的关系：

1. 机器学习可以用来作为数据挖掘的一种工具或手段；
2. 数据挖掘的手段不限于机器学习，譬如还有诸如统计学等众多方法；
3. 机器学习的应用也远不止数据挖掘，其应用领域非常广泛，譬如人工智能；

一、机器学习算法类别

1.1、分类与聚类：

Classification (分类)：给定一堆样本数据，以及这些数据所属的类别标签，通过算法来对预测新数据的类别（有先验知识）

Clustering(聚类 )：事先并不知道一堆数据可以被划分到哪些类，通过算法来发现数据之间的相似性，从而将相似的数据划入相应的类，简单地说就是把相似的东西分到一组（没有先验知识）

1.2、常见的分类与聚类算法

• 常用的分类算法：KNN最邻近算法(k-nearest neighbor，kNN)，决策树分类法，朴素贝叶斯分类算法(Naive Bayesian classifier)、支持向量机(SVM)的分类器，神经网络法，模糊分类法等等。
• 常见聚类算法： K-means聚类算法(K-means clustering)、K-MEDOIDS算法、CLARANS算法；BIRCH算法、CURE算法、CHAMELEON算法等；基于密度的方法（DBSCAN算法、OPTICS算法、DENCLUE算法等）；基于网格的方法（STING算法、CLIQUE算法、WAVE-CLUSTER算法）；

1.3、监督学习与无监督学习

机器学习按照训练数据是否有“先验知识”，一般划分为三类：

1. 监督学习(supervised learning)
2. 无监督学习(unsupervised learning)
3. 半监督学习(semi-supervised learning)

• 监督式学习技术需要关于结果的先验知识

例如，如果我们正在研究一个市场活动的历史数据，我们可以根据市场是否产生预期的反应来对数据进行分类，或决定下一步要花多少钱。监督式学习技术为预测和分类提供了强大的工具。

• 无监督学习技术不需要先验知识。

例如，在某些欺诈的案例中，只有当事情发生很久以后，我们才可能知道某次交易是不是欺诈。在这种情况下，与其试图预测哪些交易是欺诈，我们不如使用机器学习来识别那些可疑的交易，并做出标记，以备后续观察。我们对某种特定的结果缺乏先验知识、但仍希望从数据中汲取有用的洞察时，就要用到无监督式学习。

二、机器学习的应用步骤

1. 需求分析
2. 收集数据
3. 探索数据特性
4. 提取数据特征并建模[dht3] 
5. 开发代码（常用语言：R语言，Python语言，spark mllib库）
6. 训练模型[dht4] 
7. 应用系统集成（比如将训练好的算法模型集成到推荐系统中）

通用机器学习算法应用工程技术架构

三、 机器学习必需数学知识

在数据挖掘所用的机器学习算法中，很大一部分问题都可以归结为以下三个方面的数学知识：概率、距离、线性方程

3.1、概率论

朴素贝叶斯公式

          

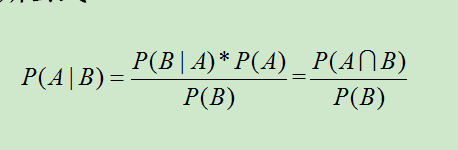
也可以简写为： 

其中:

P(A)叫做A事件的先验概率，即一般情况下，认为A发生的概率。

P(B|A)叫做似然度，是A假设条件成立的情况下发生B的概率。

P(A|B)叫做后验概率，在B发生的情况下发生A的概率，也就是要求的概率。P(B)叫做标准化常量，即在一般情况下，认为B发生的概率。

3.2、 距离（相似度）

欧式距离：也称欧几里得距离，在一个N维度的空间里，求两个点的距离，这个距离肯定是一个大于等于零的数字，那么这个距离需要用两个点在各自维度上的坐标相减，平方后加和再开方。一维，二维，三维的欧式距离计算方法：

平方欧式距离：就是欧式距离的平方。

曼哈顿距离：相比欧式距离简单的多，曼哈顿距离只要把两个点坐标的x坐标相减取绝对值，y坐标相减取绝对值，再加和， 。三维，四维以此类推。

余弦距离：也叫余弦相似度，是用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小的度量。如果两个向量的方向一致，即夹角接近零，那么这两个向量就越相近。要确定两个向量方向是否一致，要用到余弦定理计算向量的夹角。

闵可夫斯基距离：闵式距离不是一种距离，而是一组距离的定义，是对多个距离度量公式的概括性表述。两个n维变量（可以理解为n维数组，就是有n个元素）a()与b()间的闵可夫斯基距离定义为： 其中p是一个变参数，当p=1时，就是曼哈顿距离，当p=2时，就是欧式距离，当p 就是切比雪夫距离。

切比雪夫距离：国际象棋中，国王可以直行、横行、斜行。国王走一步，可以移动到相邻的8个方格的任意一个。国王从格子 到格子最少需要多少步？这个距离就是切比雪夫距离。

 

切比雪夫距离公式简单理解为就是各坐标数值差的最大值，在2维空间中的计算公式为： 。

谷本距离：同时考虑余弦距离和欧式距离的测度。

加权距离测度：可以指定某一维度的权重比例，从而使某个权重的影响力更大。

3.3、 线性方程

3.4、向量和矩阵

四、算法学习

4.1、回归算法

4.2、分类算法

4.3、聚类算法

4.4、推荐算法