题目
给出一个n行m列的的表格,表格有若干格子被涂黑,求其中最大的十字架。
要求:
(1)十字架的四个角必须是空的,下图中绿框满足条件,红框不满足条件(右上角被涂黑);

(2)十字架可以是截取的一部分(如绿框),但必须满足十字架所在的整个矩形(边长a)是正方形,且十字架可看成由五个相同的面积正方形(边长b)构成,每个角的空白区也由面积相同的正方形构成,a=3*b.如下图,红框则不满足条件。
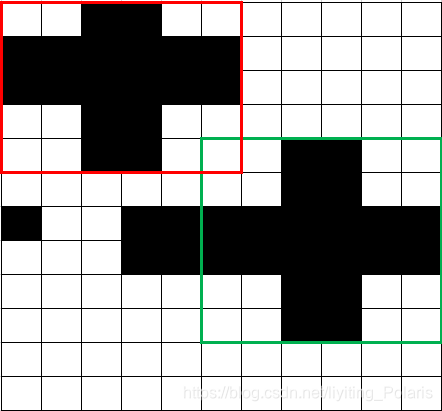
(3)如果有多个满足条件的十字架,则输出行数i最小的,若行数相等,则输出列数j最小的。(图中满足条件的十字架有两个,输出编号为“1”的十字架所在正方形左上角和右下角的坐标,如图中,输出:1 1 4 4)

样例输入:
6 6
010010
111111
010010
010010
111111
010010
输出:
1 1 3 3
说明:

输入的矩形如上图,第一行两个数字表示row行col列,接下来row行中分别表示该行的每一个格子的状态,“1”表示该格涂黑,“0”表示该格空白,输出满足上述条件的最大十字架所在的正方形左上角和右下角坐标,坐标从左上角开始计起,从左往右为1到row、从上往下为1到col.
该样例中输出的是上图标号1的绿框的左上角和右下角坐标:1 1 3 3.
分析
①我们在判断样例时,最直观的想法就是,先找边长为6的正方形,看其中黑白格子的分布是否满足条件。如过满足条件,该正方形涂黑的格子应该如图二绿色部分。我们先判断格子(1,1)是否满足条件,留空,满足条件,接下来判断格子(1,2)是否满足条件,该格应该为空,而实际上是涂黑的,不满足条件,寻找下一个边长为6的正方形,没有了,那么证明边长为6的正方形构成十字架不存在。则寻找边长为3的正方形(根据条件2,矩阵的边长一定是3的倍数)。
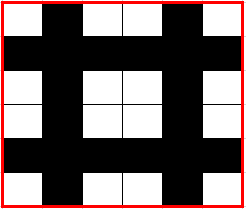

图一 图二
②寻找边长为3的正方形,看是否满足条件。判断(1,1)格满足条件,(1,2)格满足条件...
全部满足条件,输出1 1 3 3.


图三 图四
③每一次,我们都需要判断每一个格子是否满足条件,效率自然低了,有没有办法一次性判断多个格子是否满足条件?
有,把每一行、每一列连续出现多少个相同颜色的格子 这个信息存起来。
步骤:
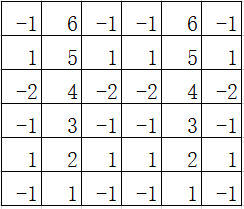
①构建一个row行col列的数组conRow[][],数组中,conRow[i][j]为正数,表示i行中,从右侧算起到序号为j格为止一共有conRow[i][j]个黑色格子;
conRow[i][j]为负数,表示i行中,从右侧算起到序号为j格为止一共有abs(conRow[i][j])个白色格子;
所以conRow为:

②同理,构建一个row行col列的数组conCol[][],数组中,conCol[i][j]为正数,表示j列中,从下侧算起到序号i格为止一共有conCol[i][j]个黑色格子;conRow[i][j]为负数,表示j列中,从下侧算起到序号i格为止一共有abs(conCol[i][j])个白色格子;
所以conCol为:
③此时,我们只需要判断正方形中某些格子的conRow、conCol值是否满足特点条件,就可以确定该正方形是否存在满足条件的十字架了。
条件就是如果正方形中存在满足条件的十字架(如图五),则绿色框内的格子conRow[i][j]一定满足conRow[i][j]>=正方形边长a,蓝色框内的格子conCol[i][j]一定满足conCol[i][j]>=正方形边长a,而红色框的格子满足条件conRow[i][j]>=a/3 和 conCol[i][j]>=a/3。
这是构成十字架的充要条件,这个时候,我们需要判断的格子的数量就从a^2减少到了a/3*2+4了,哈哈哈,是不是很开心。

图五
置于为什么conRow算连续同色格子要从右侧算起,conCol连续同色格子要从下侧算起呢?为什么不能从左侧和上侧算起呢?这是为了满足条件(3),条件(3)的要求是,如果有多个满足条件的十字架,则输出行数i最小的,若行数相等,则输出列数j最小的。这样我们就保证了左边的数大于右边,上面的数大于下面,耶~
代码如下:
import java.util.Scanner;
public class Main {
public static void main(String args[]) {
Scanner sc = new Scanner(System.in);
int row = sc.nextInt();
int col = sc.nextInt();
sc.nextLine();
int [][] arr = new int[row][col];
for(int i=0;i<row;i++){
char[] charS = sc.nextLine().toCharArray();
for(int j=0;j<col;j++){
arr[i][j] = charS[j]-'0';
}
}
int[][] conRow = new int[row][col];
int[][] conCol = new int[row][col];
int rowMax = 0;
int colMax = 0;
int count = 0;
//构建conRow和conCol
for(int i=row-1;i>-1;i--){
for(int j=col-1;j>-1;j--){
if(j==col-1||arr[i][j+1]!=arr[i][j]){
conRow[i][j] = arr[i][j]==0?-1:1;
}else{
conRow[i][j] = conRow[i][j+1] + (arr[i][j]==0?-1:1);
}
rowMax = Math.max(rowMax, conRow[i][j]);
if(i==row-1||arr[i+1][j]!=arr[i][j]){
conCol[i][j] = arr[i][j]==0?-1:1;
}else{
conCol[i][j] = conCol[i+1][j] + (arr[i][j]==0?-1:1);
}
colMax = Math.max(colMax, conCol[i][j]);
}
}
int[] res = new int[4];
for(int item:res){
item = -1;
}
//从边长最大的正方形开始判断,有则输出结果,停止,没有则边长缩小3,继续寻找
int max= Math.min(colMax, rowMax)/3*3;
Label :while(max>0){
for(int i=0;i<row;i++){
for(int j=0;j<col;j++){
if(conRow[i][j]>=max){
if(new Main().isSquare(i, j, max/3,conRow,conCol)){
res[0] = i-max/3+1;
res[1] = j+1;
res[2] = i+max/3*2;
res[3] = j+max;
break Label;
}
}
}
}
max -= 3;
}
for(int i=0;i<res.length;i++){
if(i!=0)
System.out.print(" ");
System.out.print(res[i]);
}
}
public boolean isSquare(int row1,int col1,int k,int [][]conRow, int [][]conCol){
if(row1<k||row1>conRow.length-2*k||col1>conRow[0].length-k*3){
return false;
}
//判断黑色块,绿色框内数字
for(int i=0;i<k;i++){
if(conRow[row1+i][col1]<k){
return false;
}
}
//判断黑色块,蓝色框内数字
for(int i=0;i<k;i++){
if(conCol[row1-k][col1+k+i]<k){
return false;
}
}
//判断白色块,负数
if(conRow[row1-k][col1]>0-k||conCol[row1-k][col1]>0-k||
conRow[row1+k][col1]>0-k||conCol[row1+k][col1]>0-k||
conRow[row1-k][col1+2*k]>0-k||conCol[row1-k][col1+2*k]>0-k||
conRow[row1+k][col1+2*k]>0-k||conCol[row1+k][col1+2*k]>0-k)
return false;
return true;
}
}
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








