判断两条线段是否相交

最新推荐文章于 2025-03-24 17:01:21 发布

Lindsay.Lu丶

最新推荐文章于 2025-03-24 17:01:21 发布

阅读量2.9k

点赞数 6

分类专栏：算法计算几何 C++ 文章标签： c++ 向量积计算几何线段相交算法

算法同时被 3 个专栏收录

114 篇文章

订阅专栏

C++

70 篇文章

订阅专栏

计算几何

4 篇文章

订阅专栏

1.必备知识
向量积（矢积）与数量积（标积）的区别
　　

名称	标积 / 内积 / 数量积 / 点积	矢积 / 外积 / 向量积 / 叉积
运算式（a，b和c粗体字，表示向量）	a·b=\|a\|·\|b\|cosθ	a×b=c,其中\|c\|=\|a\|·\|b\|sinθ,c的方向遵守右手定则
几何意义	向量a在向量b方向上的投影与向量b的模的乘积	c是垂直a、b所在平面，且以\|b\|sinθ为高、\|a\|为底的平行四边形的面积
运算结果的区别	标量（常用于物理）/数量（常用于数学）	矢量（常用于物理）/向量（常用于数学）

表示方法
两个向量a和b的叉积写作a×b（有时也被写成a∧b，避免和字母x混淆）。
定义
向量积可以被定义为：
模长：（在这里θ表示两向量之间的夹角(共起点的前提下)（0° ≤ θ ≤ 180°），它位于这两个矢量所定义的平面上。）
这里写图片描述
方向：a向量与b向量的向量积的方向与这两个向量所在平面垂直，且遵守右手定则。
（一个简单的确定满足“右手定则”的结果向量的方向的方法是这样的：若坐标系是满足右手定则的，当右手的四指从a以不超过180度的转角转向b时，竖起的大拇指指向是c的方向。）

也可以这样定义（等效）：
向量积|c|=|a×b|=|a|·|b|sin< a,b >
即c的长度在数值上等于以a，b，夹角为θ组成的平行四边形的面积。
而c的方向垂直于a与b所决定的平面，c的指向按右手定则从a转向b来确定。
*运算结果c是一个伪向量。这是因为在不同的坐标系中c可能不同。

这里写图片描述

2.[C++] 这里写图片描述

代码：

using namespace std;  
struct point  
{  
    double x,y;  
};  
struct segment  
{  
    point begin,end;  
};  
double min(double x,double y)  
{  
    return x<y ? x:y;  
}  
double max(double x,double y)  
{  
    return x>y ? x:y;  
}  
bool onsegment(point pi,point pj,point pk) //判断点pk是否在线段pi pj上   
{  
    if(min(pi.x,pj.x)<=pk.x && pk.x<=max(pi.x,pj.x))  
    {  
        if(min(pi.y,pj.y)<=pk.y && pk.y<=max(pi.y,pj.y))  
        {  
            return true;  
        }  
    }  
    return false;  
}  
double direction(point pi,point pj,point pk) //计算向量pkpi和向量pjpi的叉积   
{  
    return (pi.x-pk.x)*(pi.y-pj.y)-(pi.y-pk.y)*(pi.x-pj.x);  
}  
bool judge(point p1,point p2,point p3,point p4) //判断线段p1p2和p3p4是否相交   
{  
    double d1 = direction(p3,p4,p1);  
    double d2 = direction(p3,p4,p2);  
    double d3 = direction(p1,p2,p3);  
    double d4 = direction(p1,p2,p4);  
    if(d1*d2<0 && d3*d4<0)  
        return true;  
    if(d1==0 && onsegment(p3,p4,p1))  
        return true;  
    if(d2==0 && onsegment(p3,p4,p2))  
        return true;  
    if(d3==0 && onsegment(p1,p2,p3))  
        return true;  
    if(d4==0 && onsegment(p1,p2,p4))  
        return true;  
    return false;  
}  
int main()  
{  
    int n,count;  
    segment seg[101];  
    while(cin>>n&&n)  
    {  
        count = 0;  
        for(int i=1; i<=n; i++)  
        {  
            cin>>seg[i].begin.x>>seg[i].begin.y>>seg[i].end.x>>seg[i].end.y;  
        }  
        for(int i=1; i<n; i++)  
            for(int j=i+1; j<=n; j++)  
            {  
                if(judge(seg[i].begin,seg[i].end,seg[j].begin,seg[j].end))  
                {  
                    count++;  
                }  
            }  
            cout<<count<<endl;  
    }  
    return 0;  
}

3.[C++]计算几何之判断线段相交
给定两个点:

typedef  struct {

  double  x, y;

} Point;

Point A1,A2,B1,B2;

首先引入两个实验：

a.快速排斥实验
设以线段A1A2和线段B1B2为对角线的矩形为M,N;
若M,N 不相交，则两个线段显然不相交；
所以：满足第一个条件时：两个线段可能相交。

b.跨立实验
如果两线段相交，则两线段必然相互跨立对方.若A1A2跨立B1B2，则矢量( A1 - B1 ) 和(A2-B1)位于矢量(B2-B1)的两侧，

这里写图片描述
即(A1-B1) × (B2-B1) * (A2-B1) × (B2-B1)<0。
上式可改写成(A1-B1) × (B2-B1) * (B2-B1) × (A2-A1)>0。
应该判断两次，即两条线段都要为直线，判断另一直线的两端点是否在它两边，若是则两线段相交。
若积极满跨立实验是不行的，如下面的情况：
这里写图片描述

即两条线段在同一条直线上。所以我们要同时满足两次跨立和快速排斥实验。

总体分析：
当(A1-B1) × (B2-B1)=0时，说明(A1-B1)和(B2-B1)共线，但是因为已经通过快速排斥试验，所以 A1一定在线段 B1B2上；同理，(B2-B1)×(A2-B1)=0 说明A2一定在线段B1B2上。所以判断A1A2跨立B1B2的依据是：(A1-B1) × (B2-B1) * (B2-B1) × (A2-B1) >= 0。
同理判断B1B2跨立A1A2的依据是：(B1-A1) × (A2-A1) * (A2-A1) × (B2-A1) >= 0。

如图：
这里写图片描述

应用：
1. 判断两个线段相交
2. 判断线段与直线相交
3. 判断点在矩形内

代码：

/* 
(A1-B1) × (B2-B1) * (B2-B1) × (A2-A1) >= 0 
(B1-A1) × (A2-A1) * (A2-A1) × (B2-A1) >= 0 
*/  

#include<stdio.h>  
#define min(a,b) a<b?a:b  
#define max(a,b) a>b?a:b  
typedef struct {  
double x,y;  
}Point;  
Point A1,A2,B1,B2;  
Point  A1B1, B2B1, A2A1, B2A1;  
double xx(Point &s,Point &t)  
{  
    return (s.x*t.y+s.y*t.x);  
}  
int kua()                           //跨立实验  
{  
    A1B1.x=A1.x-B1.x;  A1B1.y=A1.y-B1.y;  
    B2B1.x=B2.x-B1.x;  B2B1.y=B2.y-B1.y;  
    A2A1.x=A2.x-A1.x;  A2A1.y=A2.y-A1.y;  
    B2A1.x=B2.x-A1.x;  B2A1.y=B2.y-A1.y;  
    if(xx(A1B1,B2B1) * xx(B2B1,A2A1)>=0)  
    {  
        A1B1.y=-A1B1.y;A1B1.x=-A1B1.x;  
        if(xx(A1B1,A2A1) * xx(A2A1,B2A1)>=0)  
            return 1;  
        else  
            return 0;  
    }  
    else  
        return 0;  
}  
int main()  
{  
    Point A1,A2,B1,B2;  
    int flag=1,i,j,a,b,c,d,e,f;  
    while(1)  
    {  
        scanf("%lf%lf%lf%lf", &A1.x, &A1.y, &A2.x, &A2.y);  
        scanf("%lf%lf%lf%lf", &B1.x, &B1.y, &B2.x, &B2.y);  
        if( min(A1.x,A2.x) <= max(B1.x,B2.x) &&  
            min(B1.x,B2.x) <= max(A1.x,A2.x) &&  
            min(A1.y,A2.y) <= max(B1.y,B2.y) &&  
            min(B1.y,B2.y) <= max(A1.y,A2.y)   )   //快速排斥实验  
        {  
            if(kua())  
                printf("线段相交\n");  
            else  
                printf("线段不相交\n");  
        }  
        else  
            printf("线段不相交\n");  

    }  
    return 0;  
}

4.[CAD]
判断两条线段是否相交，可以采用向量积的方式来判断，如下图所示：
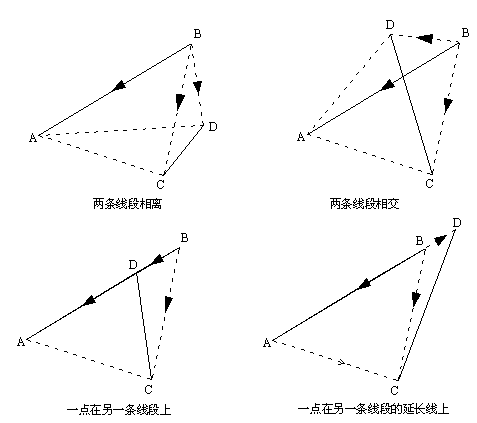
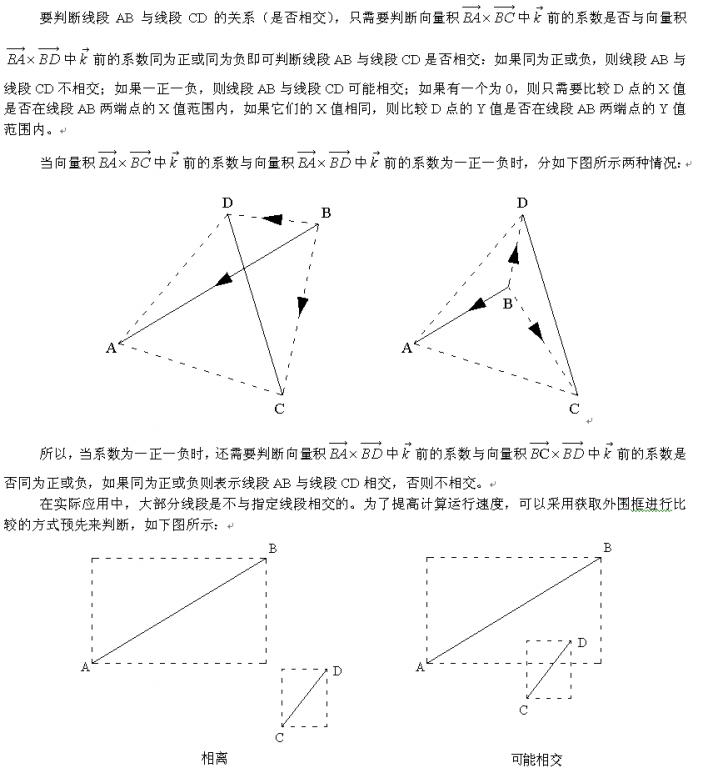
这里写图片描述

这里写图片描述

现定义一个函数初步判断两线段是否相交，如下代码：

/// <summary>
/// 初步根据外围框大致判断两条线段是否相交
/// </summary>
/// <param name="line01Coords">线段1的坐标，长度为6</param>
/// <param name="line02Coords">线段2的坐标，长度为6</param>
/// <returns>返回类型为bool，如果为true表示两条线段可能相交，如果为false表示两条线段不相交</returns>
private bool JudgeAboutCrossStatus(double[] line01Coords, double[] line02Coords)
{
    bool returnResult = true;
    //先判断在XY方向的最值
    double maxX1, minX1, maxY1, minY1;
    maxX1 = minX1 = line01Coords[0];
    maxY1 = minY1 = line01Coords[1];
    if (line01Coords[0] < line01Coords[3])
        maxX1 = line01Coords[3];
    else
        minX1 = line01Coords[3];
    if (line01Coords[1] < line01Coords[4])
        maxY1 = line01Coords[4];
    else
        minY1 = line01Coords[4];
    double maxX2, minX2, maxY2, minY2;
    maxX2 = minX2 = line02Coords[0];
    maxY2 = minY2 = line02Coords[1];
    if (line02Coords[0] < line02Coords[3])
        maxX2 = line02Coords[3];
    else
        minX2 = line02Coords[3];
    if (line02Coords[1] < line02Coords[4])
        maxY2 = line02Coords[4];
    else
        minY2 = line02Coords[4];
    //比较最值大小
    if ((minX1 > maxX2) || (maxX1 < minX2) || (minY1 > maxY2) || (maxY1 < minY2))
    {
        returnResult = false;
    }
    return returnResult;
}
函数JudgeAboutCrossStatus()如果返回值为true则表示两条线段可能相交，则需要采用向量积的方式来判断是否相交，如果为false则表示两条线段不相交。现在定义一个函数Judge2LinesRelation ()用于判断两条线段是否相交，其代码如下：
/// <summary>
/// 判断两条线段是否相交
/// </summary>
/// <param name="line01Coords">线段1的坐标，长度为6</param>
/// <param name="line02Coords">线段2的坐标，长度为6</param>
/// <returns>返回类型为bool，如果为true表示两条线段相交，如果为false表示两条线段不相交</returns>
private bool Judge2LinesRelation(double[] line01Coords, double[] line02Coords)
{
    bool returnResult = true;
    returnResult = JudgeAboutCrossStatus(line01Coords, line02Coords);
    if (returnResult)//初步判断两条线段可能相交
    {
        double BAx, BAy, BCx, BCy, BDx, BDy, BABCk, BABDk;
        BAx = line01Coords[0] - line01Coords[3];
        BAy = line01Coords[1] - line01Coords[4];
        BCx = line02Coords[0] - line01Coords[3];
        BCy = line02Coords[1] - line01Coords[4];
        BABCk = BAx * BCy - BAy * BCx;
        BDx = line02Coords[3] - line01Coords[3];
        BDy = line02Coords[4] - line01Coords[4];
        BABDk = BAx * BDy - BAy * BDx;
        if (((BABCk > 0) && (BABDk > 0)) || ((BABCk < 0) && (BABDk < 0)))
        {
            returnResult = false;
        }
        else if (((BABCk > 0) && (BABDk < 0)) || ((BABCk < 0) && (BABDk > 0)))
        {
            double BCBDk;
            BCBDk = BCx * BDy - BCy * BDx;
            if (((BABDk > 0) && (BCBDk > 0)) || ((BABDk < 0) && (BCBDk < 0)))
            {
                returnResult = true;
            }
            else
            {
                returnResult = false;
            }                   
        }
        else if ((BABCk == 0)||(BABDk==0))//点C或D在直线AB上
        {
            double[] templine02Coords = new double[3];
            if (BABCk == 0)//点C在直线AB上
            {
                templine02Coords[0] = line02Coords[0];
                templine02Coords[1] = line02Coords[1];
                templine02Coords[2] = line02Coords[2];
            }
            else//点D在直线AB上
            {
                templine02Coords[0] = line02Coords[3];
                templine02Coords[1] = line02Coords[4];
                templine02Coords[2] = line02Coords[5];
            }
            if (line01Coords[0] == line01Coords[3])//是否垂直，是则比较Y值
            {
                double maxY, minY;
                maxY = minY = line01Coords[1];
                if (line01Coords[1] < line01Coords[4])
                    maxY = line01Coords[4];
                else
                    minY = line01Coords[4];
                if ((templine02Coords[1] >= minY) && (templine02Coords[1] <= maxY))//在线段上
                    returnResult = true;
                else
                    returnResult = false;
            }
            else //比较X值
            {
                double maxX, minX;
                maxX = minX = line01Coords[0];
                if (line01Coords[0] < line01Coords[3])
                    maxX = line01Coords[3];
                else
                    minX = line01Coords[3];
                if ((templine02Coords[0] >= minX) && (templine02Coords[0] <= maxX))//在线段上
                    returnResult = true;
                else
                    returnResult = false;
            }
        }
    }
    return returnResult;
}