介绍
这里讲的顶点对之间的最短路径是基于动态规划在图中的实现。每一个循环都类似矩阵乘法,因此这个算法看起来就像是一直在做矩阵乘法。
实现
在这里我们用邻接矩阵表示法来表示一个图,因为相对邻接表来说,邻接矩阵表示要容易些,并且采用自底而下的算法来计算最短路径权重。
typedef int (*Metrix)[VERTEX_NUMBER];
void printfMatrix(Metrix graphmetrix)
{
for (int x = 0; x < VERTEX_NUMBER; ++ x)
{
for (int y = 0; y < VERTEX_NUMBER; ++ y)
{
cout << "\t" << graphmetrix[x][y] << " ";
}
cout << endl;
}
cout << endl;
}这是输出一个图的矩阵表示法,其中的每个值表示当中两个顶点之间的权重值。
int getSentinel()
{
return 0x7fffffff;
}
Metrix entendShortestPaths(Metrix left, Metrix right)
{
const int n = VERTEX_NUMBER;
int *graph = new int[n * n];
Metrix c = (int(*)[n])graph;
for (int i = 0; i < n; ++ i)
{
for (int j = 0; j < n; ++ j)
{
c[i][j] = getSentinel();
for (int k = 0; k < n; ++ k)
{
if (getSentinel() != left[i][k] && getSentinel() != right[k][j])
{
c[i][j] = std::min(c[i][j], left[i][k] + right[k][j]);
}
}
}
}
return c;
}在计算时,我们首先把结果矩阵里面的值均初始化为最大,然后再计算它和当前两个结点权重之间的最小值,返回的最小值就是两个顶点之间的最小权重。在这里,left[i][k]就是结点i->k的最短路径值,然后,right[k][j]就是k->j的最小权重值,把2个相加就是i->j的最小权重值。接着来看看矩阵乘法的算法:
Metrix squareMatrixMultiply(Metrix left, Metrix right)
{
const int n = VERTEX_NUMBER;
int *graph = new int[n * n];
Metrix c = (int(*)[n])graph;
for (int i = 0; i < n; ++ i)
{
for (int j = 0; j < n; ++ j)
{
c[i][j] = 0;
for (int k = 0; k < n; ++ k)
{
c[i][j] += left[i][k] * right[k][j];
}
}
}
return c;
}是不是和上面的算法很相似呢。这里计算c[i][j]的值就是left矩阵的第i行的值乘以right的第j列的所有值的结果的总和。
然后,计算最短路径有2种方法,慢速的和快速的,其中快速的是在慢速的基础上做优化。先来看看慢速的如何计算:
Metrix slowAllPairsShortestPaths(Metrix graph)
{
const int n = VERTEX_NUMBER;
int *tmp = new int[n * n];
Metrix c = (int(*)[n])tmp;
memcpy(c, graph, n * n * sizeof(4));
for (int m = 1; m < n - 1; ++ m)
{
Metrix p = entendShortestPaths(c, graph);
delete [] c;
c = p;
printfMatrix(c);
}
return c;
}我们在每次扩展最短路径的结果中,把返回的结果矩阵继续和原始矩阵做扩展,直到计算n-1次为止。而在这个算法上做的优化则是:因为我们的目的只是需要得出n-1次的最后结果,而不关心中间结果。所以我们可以每次进行m*2操作来让m的值进行递增,而不是m+1。
Metrix fasterAllPairsShortestPaths(Metrix graph)
{
const int n = VERTEX_NUMBER;
int *tmp = new int[n * n];
Metrix c = (int(*)[n])tmp;
memcpy(c, graph, n * n * sizeof(4));
int m = 1;
while (m < n - 1)
{
Metrix p = entendShortestPaths(c, c);
delete [] c;
c = p;
printfMatrix(c);
m *= 2;
}
return c;
}我们可以来看看最短路径的图解过程:
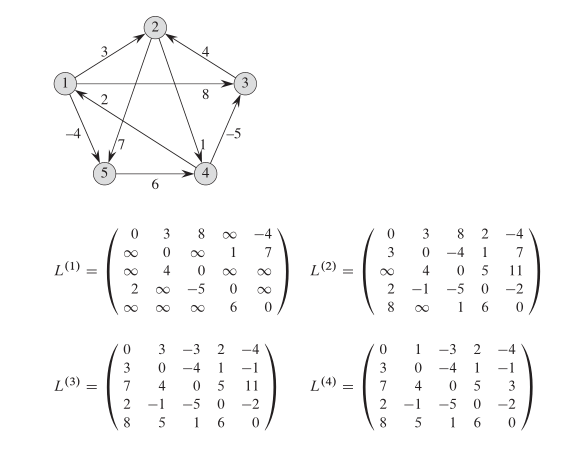
慢速最短路径图解过程
而我们再来测试下慢速和快速的运行结果,也使用上图中一样的图:
int _tmain(int argc, _TCHAR* argv[])
{
copyright();
cout << getSentinel() << endl;
cout << "directed adjacency matrix: " << endl;
int graphmetrix[VERTEX_NUMBER][VERTEX_NUMBER] =
{
{0, 3, 8, 0x7fffffff, -4},
{0x7fffffff, 0, 0x7fffffff, 1, 7},
{0x7fffffff, 4, 0, 0x7fffffff, 0x7fffffff},
{2, 0x7fffffff, -5, 0, 0x7fffffff},
{0x7fffffff, 0x7fffffff, 0x7fffffff, 6, 0},
};
cout << "directed weight graph structure: " << endl;
for (int x = 0; x < VERTEX_NUMBER; ++ x)
{
cout << "vertex " << x + 1 << ";";
for (int y = 0; y < VERTEX_NUMBER; ++ y)
{
if (0 != graphmetrix[x][y])
{
cout << y + 1 << " ";
}
}
cout << endl;
}
cout << "origin: " << endl;
printfMatrix(graphmetrix);
cout << "slow algorithm: " << endl;
Metrix c = slowAllPairsShortestPaths(graphmetrix);
delete [] c;
cout << "faster algorithm: " << endl;
c = fasterAllPairsShortestPaths(graphmetrix);
delete [] c;
return 0;
}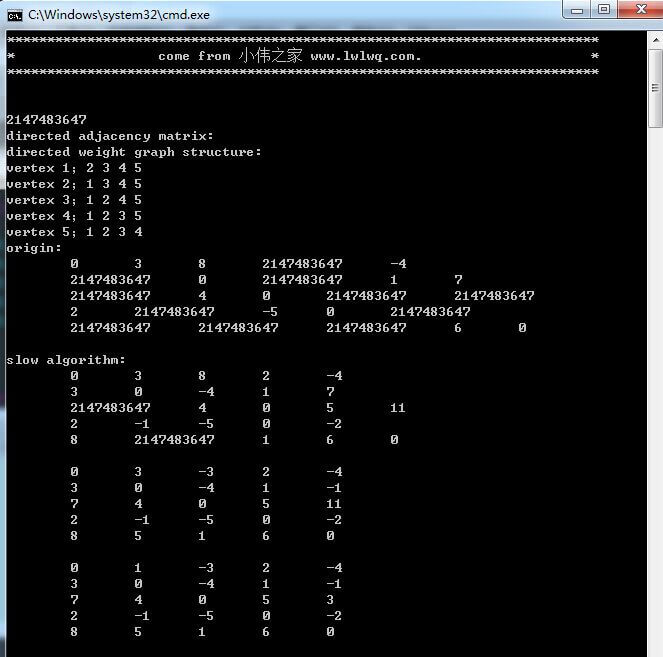
慢速最短路径运行结果
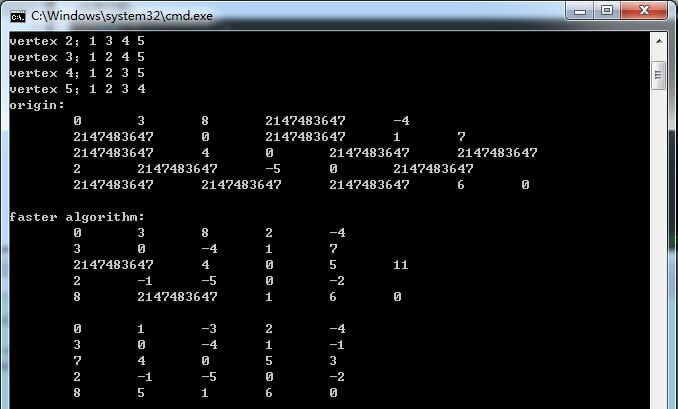
快速最短路径运行结果
从结果中可以看出,快速的比慢速的要快,而且这是在结点数量少的情况,如果是结点数量多的情况,优化效果是很显示的,计算量要少很多。






















 715
715

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










