堆排序与Top-K：一场数据“金字塔”的建造与拆解

已于 2025-02-05 16:53:15 修改
阅读量630 收藏 28
点赞数 9
文章标签： 算法 数据结构 开发语言 c语言 排序算法
于 2025-02-05 16:47:41 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/ll778811/article/details/145445730
版权

目录

一.堆排序

1.借助数据结构堆实现

分析 

2.借助堆思想实现

建堆 

向下调整算法建堆

向上调整算法建堆

排序 

3.两种排序方法比较

二.Top-K问题

1.介绍

2.解决思想

3.实现

三.总结

        本期我们将介绍堆排序的不同实现方法，并借助堆的思想解决Top-K问题。

一.堆排序

        在前面的学习中，我们可以通过冒泡排序和快速排序来对无序数组进行降序和升序的排序，但能否借助堆来对数组进行排序呢？

1.借助数据结构堆实现

void HeapSort(int* a, int n)

        堆排序函数参数为指向数组的指针和数组的元素个数。

Heap hp;
HeapInit(&hp);
int i = 0;
//建堆
for (int i = 0; i < n; i++)
{
	HeapPush(&hp, a[i]);
}

        首先数组中的元素现在并不是对结构，所以我们先要建堆，然后让数组中的元素入堆。      

while (!HeapEmpty(&hp))
{
	int top = HeapTop(&hp);
	a[i++] = top;
	HeapPop(&hp);
}

         当堆不为空时，循环取堆顶元素，放入数组中，再让对顶元素出堆，跳出循环后，此时数组已经变成一个降序或升序的数组，降序和升序取决于建堆中的调整算法，若建的是大堆，那么此时数组为降序，若建的是小堆，那么此时数组为升序。

完整堆排序代码：

void HeapSort01(int* a, int n)
{
	Heap hp;
	HeapInit(&hp);
	int i = 0;
	//建堆
	for (int i = 0; i < n; i++)
	{
		HeapPush(&hp, a[i]);
	}

	while (!HeapEmpty(&hp))
	{
		int top = HeapTop(&hp);
		a[i++] = top;
		HeapPop(&hp);
	}
}
分析 

        这种堆排序的前提是必须先要有堆这个数据结构，必须基于数据结构堆的实现。             

2.借助堆思想实现

void HeapSort(int* a, int n)
建堆 

        在这里对数组建堆有两种思想：

向下调整算法建堆

        以建大堆为例：

        若现在有这样的一个数组，将它转化为如图的二叉树，若使用向下调整，我们需要调整每一颗二叉树。

        如图，调整顺序依次为以10，20，17为根节点的子树：

        调整完成后，即可得到大堆。

        孩子结点用n表示为：n-1，则当前子树的父结点用n表示为:（n-1-1)/2

向下调整建堆代码：

for (int i = (n - 2) / 2; i >= 0; i--)
{
	AdjustDown(a, i, n);
}
void AdjustDown(HPDataType* arr,int parent,int n)
{
	int child = 2 * parent + 1;
	while (child < n)
	{
		//大堆: <
		//小堆: >
		if (child + 1 < n && arr[child] < arr[child + 1])
		{
			child++;
		}
		//大堆: >
		//小堆: <
		if (arr[child] > arr[parent])
		{
			Swap(&arr[child], &arr[parent]);
			parent = child;
			child = 2 * parent + 1;
		}
		else
		{
			break;
		}
	}
}
向上调整算法建堆

        还是以建大堆为例：

        由于是向上调整，在获取孩子结点后，需要从上到下对每棵子树进行调整。

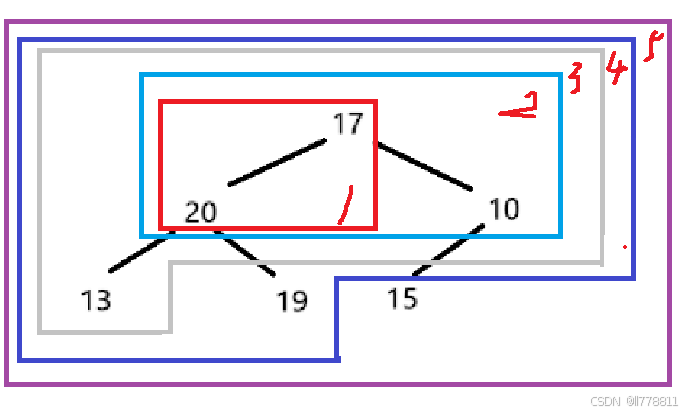 图示：

        调整完成后，即可得到大堆。

        孩子结点从0开始，不超过n

向上调整建堆代码：

for (int i = 0; i < n; i++)
{
	AdjustUp(a, i);
}
void AdjustUp(HPDataType* arr, int child)
{
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		//大堆: >
		//小堆: <
		if (arr[child] > arr[parent])
		{
			Swap(&arr[child], &arr[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}
排序 

        在建完堆之后我们进行排序：

        我们可以每次将堆顶的元素和堆底最后一个元素交换，并对剩下的n-1个元素进行向下调整，循环操作直至n-1为0。

        依旧以大堆为例：

        可以看到建堆为大队排序后，最终的数组为升序的数组，以此类推，建小堆，最终的数组为降序。

排序代码：

int end = n - 1;
while (end > 0)
{
	Swap(&a[0], &a[end]);
	AdjustDown(a, 0, end);
	end--;
}

完整堆排序代码：        

void HeapSort(int* a, int n)
{
	for (int i = (n - 2) / 2; i >= 0; i--)
	{
		AdjustDown(a, i, n);
	}

	int end = n - 1;
	while (end > 0)
	{
		Swap(&a[0], &a[end]);
		AdjustDown(a, 0, end);
		end--;
	}
}

3.两种排序方法比较

        第二种堆排序的实现方式借助了堆思想，不再依靠堆这种数据结构，相较第一种而言，更加高效。

二.Top-K问题

1.介绍

        Top-K问题是指求数据结合中前K个最⼤的元素或者最⼩的元素，⼀般情况下数据量都⽐较⼤。 ⽐如：专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。

2.解决思想

        对于Top-K问题，最先想到的是遍历排序，但当数据量非常大时，在执行时可能会由于内存的限制而无法解决，所以在这里我们最好借助堆去解决。

        首先，以大堆为例，取数据中前K个数据进行建堆。

          建完堆后，⽤剩余的N-K个元素依次与堆顶元素来⽐较，若元素比堆顶元素小就入堆，替换堆顶元素。

        以此类推可以得到以下结论：

        找最大的前K个元素，建小堆，比堆顶元素大就入堆。

        找最小的前K个元素，建大堆，比堆顶元素小就入堆。

3.实现

创造数据

void CreateNDate()
{
	// 造数据
	int n = 10000;
	srand((unsigned int)time(0));
	const char* file = "data.txt";
	FILE* fin = fopen(file, "w");
	if (fin == NULL)
	{
		perror("fopen error");
		return;
	}

	for (size_t i = 0; i < n; ++i)
	{
		int x = rand() % 1000000;
		fprintf(fin, "%d\n", x);
	}

	fclose(fin);
}

        在这里使用这个函数创造10000个随机数保存在文件中。

int k = 0;
scanf("%d", &k);

const char* file = "data.txt";
FILE* fout = fopen(file, "r");
if (fout == NULL)
{
	perror("fopen");
	exit(1);
}

·        在创建完数据后，我们让用户输入k的大小，并打开刚刚存放数据的文件，准备读入数据。

int* minHeap = (int*)malloc(k * sizeof(int));
for (int i = 0; i < k; i++)
{
	fscanf(fout,"%d", &minHeap[i]);
}

//建堆
for (int i = (k - 1 - 1) / 2; i >= 0; i--)
{
	AdjustDown(minHeap, i, k);
}

         以找前K个最大的数据为例，我们建小堆，将文件中前K个数据导入数组中，并根据数组向下调整并建堆。

int x = 0;
while (fscanf(fout, "%d", &x) != EOF)
{
	if (x > minHeap[0])
	{
		minHeap[0] = x;
		AdjustDown(minHeap, 0, k);
	}
}

        建完堆后，我们让堆顶和剩余的n-k个数据进行比较，入堆，并向下调整使堆顶始终为堆中的最小值。

for (int i = 0; i < k; i++)
{
	printf("%d ", minHeap[i]);
}
fclose(fout);

        最后将堆打印并关闭文件，这样就能找出这些数据中的前K个最大值。

完整代码：

void CreateNDate()
{
	// 造数据
	int n = 10000;
	srand((unsigned int)time(0));
	const char* file = "data.txt";
	FILE* fin = fopen(file, "w");
	if (fin == NULL)
	{
		perror("fopen error");
		return;
	}

	for (size_t i = 0; i < n; ++i)
	{
		int x = rand() % 1000000;
		fprintf(fin, "%d\n", x);
	}

	fclose(fin);
}

void TopK()
{
	int k = 0;
	scanf("%d", &k);

	const char* file = "data.txt";
	FILE* fout = fopen(file, "r");
	if (fout == NULL)
	{
		perror("fopen");
		exit(1);
	}

	int* minHeap = (int*)malloc(k * sizeof(int));
	for (int i = 0; i < k; i++)
	{
		fscanf(fout,"%d", &minHeap[i]);
	}

	//建堆
	for (int i = (k - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(minHeap, i, k);
	}

	int x = 0;
	while (fscanf(fout, "%d", &x) != EOF)
	{
		if (x > minHeap[0])
		{
			minHeap[0] = x;
			AdjustDown(minHeap, 0, k);
		}
	}

	for (int i = 0; i < k; i++)
	{
		printf("%d ", minHeap[i]);
	}
	fclose(fout);
}

三.总结

        本期我们通过借助堆的思想实现了堆排序并解决了Top-K问题，下一期我们将实现链式结构的二叉树。

ll778811
关注
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值