【算法+工程】单纯形法.md

一、优化问题标准型

1.1 问题例子

某工厂在计划期内要安排生产Ⅰ、Ⅱ两种产品 , 已知生产单位产品所需的设备台时及A、B两种原材料的消耗 , 如表1-1所示。

该工厂每生产一件产品Ⅰ可获利2元 , 每生产一件产品Ⅱ可获利3元 , 问应如何安排计划使该工厂获利最多 ?

1.2 数学形式

上述问题可以用以下形式表示，其中$x_1$、$x_2$分别表示生产Ⅰ、Ⅱ产品的个数：
目标函数：
$$max(z=2\ast x_1+3\ast x_2)$$
约束条件：
$$\{\begin{array}{rlrlr}{x}_1& +& 2\ast x_2& ⩽& 8\\ 4\ast x_1& & & ⩽& 16\\ & & 4\ast x_2& ⩽& 12\\ x_1& ,& x_2& ⩾& 0\end{array}$$

1.3 标准型

线性规划的标准型：
目标函数：
$$max(z=c_1\ast x_1+c_2\ast x_2+...+c_n\ast x_n)$$
约束条件：
$$\{\begin{array}{rl}{a}_1\ast x_1+a_2\ast x_2+& ...+a_n\ast x_n=b_1\\ a_1\ast x_1+a_2\ast x_2+& ...+a_n\ast x_n=b_2\\ & ...\\ a_1\ast x_1+a_2\ast x_2+& ...+a_n\ast x_n=b_m\\ x_1,x_2,& ...,x_n⩾0\end{array}$$
标准型，要求是，目标函数为：max，约束条件中的$b_i$均为正，变量均为$⩾0$

1.4 转化为标准型

将1.2的数学表达式变为1.3的标准型。在不等式中加入松弛变量，可以使得不等式变为等式。
目标函数：
$$max(z=2\ast x_1+3\ast x_2+0\ast x_3+0\ast x_4+0\ast x_5)$$
约束条件：
$$\{\begin{array}{rlrlrlrlrlr}{x}_1& +& 2\ast x_2& +& x_3& & & & & =& 8\\ 4\ast x_1& & & & & +& x_4& & & =& 16\\ & & 4\ast x_2& & & & & +& x_5& =& 12\\ x_1& ,& x_2& ,& x_3& ,& x_4& ,& x_5& ⩾& 0\end{array}$$

二、单纯形法

2.1 单纯形法思路

将上述问题化为标准型后，可以得到系数矩阵：
$$A=(P_1,P_2,P_3,P_4,P_5)=\left(\begin{array}{ccccc}1& 2& 1& 0& 0\\ 4& 0& 0& 1& 0\\ 0& 4& 0& 0& 1\end{array}\right)$$
其中，$P_3,P_4,P_5$是线性独立的 , 这些向量构成一个基，对应的$x_3,x_4,x_5$称为基变量。则，$x_1,x_2$称为非基变量。

单纯形法的大致思路是：
1、通过线性变换，将非基变量替换基变量，进而做到仅使用非基变量来表示目标函数。因为变量的值域为$⩾0$，所以当非基变量表示目标函数的对应系数均为负数时候，可以得到目标变量的最大值，即为非基变量取0值的时候。
2、当不满足非基变量的系数均为负的时候，需要把一个基变量改成非基变量，相应的该非基变量也为基变量。换出规则：优先将非基变量正系数较大的替换；换入规则：保证替换后的其余变量均为非负值的基变量。

2.2 单纯形法步骤

（1）选出基变量和非基变量
在上面的例子中：
基变量：$x_3,x_4,x_5$。
非基变量：$x_1,x_2$。
（2）将基变量用非基变量表示
$$\{\begin{array}{rl}{x}_3& =8-x_1-2\ast x_2\\ x_4& =16-4\ast x_1\\ x_5& =12-4\ast x_2\end{array}$$
（3）非基变量带入目标函数
$$z=2\ast x_1+3\ast x_2$$
（4）令非基变量为0，得到一组可行解，边界值
$$(0,0,8,16,12)$$
（5）确定换出变量
因为目标函数的非基变量均为正值，所以没达到最优解，选非基变量中系数较大的$x_2$为换出变量，即在下轮计算中，把$x_2$为作为基变量
（6）确定换入变量
确定$x_2$为换出变量后，需要从原来的基变量中为换入变量。令$x_1=0$，(因为在确定可行解的时候，非基变量取0)，保证其他变量$⩾0$。
$$\{\begin{array}{rl}{x}_3& =8-2\ast x_2⩾0\\ x_4& =16⩾0\\ x_5& =12-4\ast x_2⩾0\end{array}$$
当，$x_2=min(8/2,-,12/4)=3$时候，成立，所以，用$x_2$去替换$x_5$。即为$x_5$为换出变量。
（7）迭代重复（2）、（3）、（4）、（5）、（6）
$x_5$替换$x_2$的结果，可行解：$(0,3,2,16,0)$
$$z=9+2\ast x_1-\frac{3}{4}{x}_5$$
不满足，于是继续迭代，得到：可行解：$(2,3,0,8,0)$；再次迭代得到：可行解：$(4,2,0,0,4)$，此时的目标函数：
$$z=14-1.5x_3-0.125x_4$$
满足结束条件：
所以。结果，可行解：$(4,2,0,0,4)$，目标最大值：14。产品Ⅰ生产4件，产品Ⅱ生产2件，利润最大。

2.3 单纯形法表格形式

看了上面的过程，能够总结到单纯形法的解法步骤，并且通过表格形式表达，在使用表格之前，需要一些推导。

表格公式推导

标准型的目标函数如下：
$$max(z=c_1{x}_1+c_2{x}_2+...+c_n{x}_n)$$
基变量有m个，假设前m个即为基变量。通过线性变换后，可以得到如下表达式：
$$\{\begin{array}{rl}{x}_1+a_{1,m+1}{x}_{m+1}+& ...+a_{1,n}{x}_n=b_1\\ x_2+a_{2,m+1}{x}_{m+1}+& ...+a_{2,n}{x}_n=b_2\\ & ...\\ x_m+a_{m,m+1}{x}_{m+1}+& ...+a_{m,n}{x}_n=b_m\end{array}$$
$x_1,...,x_m$为基变量，$x_{m+1},...,x_n$为非基变量。
使用非基变量来表示基变量$x_i$。
$$x_i=b_i-\sum _{j=m+1}^n{a}_{i,j}{x}_j$$
带入目标函数中：
$$z=c_1{x}_1+c_2{x}_2+...+c_n{x}_n=z_0+\sum _{j=m+1}^n(c_j-z_j)x_j$$
其中，
$$z_j=\sum _{i=1}^m{c}_i{a}_{i,j}$$
$$z_0=\sum _{i=1}^m{c}_i{b}_i$$
记：
$${\theta }_j=c_j-z_j$$

通过将公式与步骤对照，可以知道，${\theta }_j$即为目标函数用非基变量表示后的各个系数，用它来判断是否为最优解。
而$z_0$即为最优解的max值（令非基变量均为0）。

表格形式表示

这里我的表格形式和网上的有一点区别，但是本质一样，这么写是为了之后代码实现方便看：
（1）系数矩阵

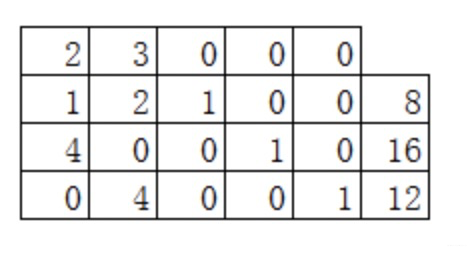
第1行是：目标函数的系数向量；
第2~4行是：标准型约束条件的矩阵；
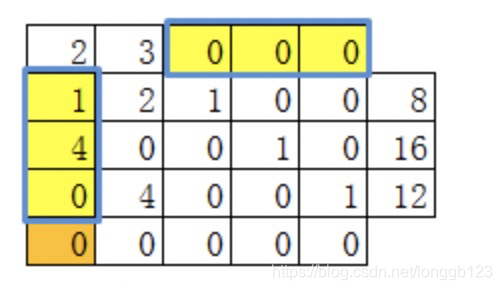
（2）计算$z_j$值

根据上面的公式，可以知道$z_j={\sum }_{i=1}^m{c}_i{a}_{i,j}$是由基变量的目标函数系数向量和对应的变量的标准型约束列系数相乘得来的。
第5行是：计算的$z_j$值。
（3）计算${\theta }_j$值

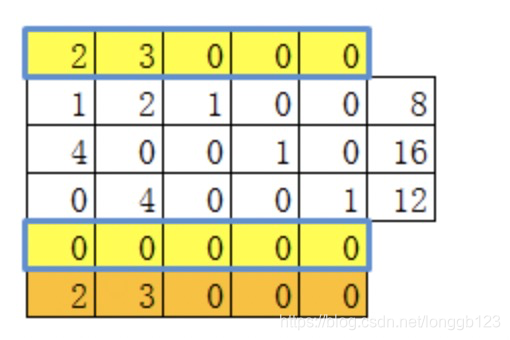
根据上面的公式，可以知道${\theta }_j=c_j-z_j$。所以得到了新的替换后的目标函数由非基变量表示的系数向量。
第5行是：计算的${\theta }_j=c_j-z_j$值。
（4）确定换出、换入

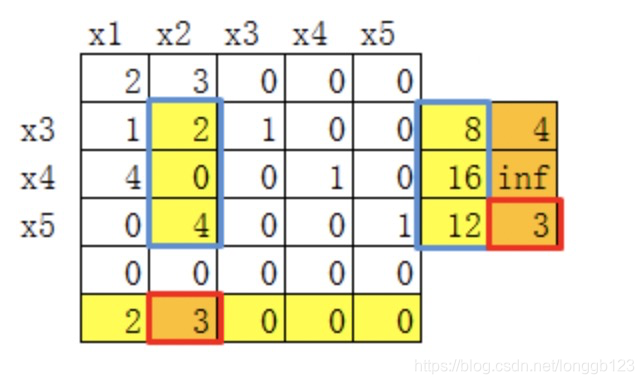
在第5行中，找到正系数最大的为换入变量，该列的系数，使用标准型约束矩阵的常数向量列除以它，得到第7列。第7列中正最小的数为换出变量。
图中2个红框表示找到的换入、换出变量。
换出变量是$x_5$，换入变量是$x_2$。
（5）求出此时的目标值

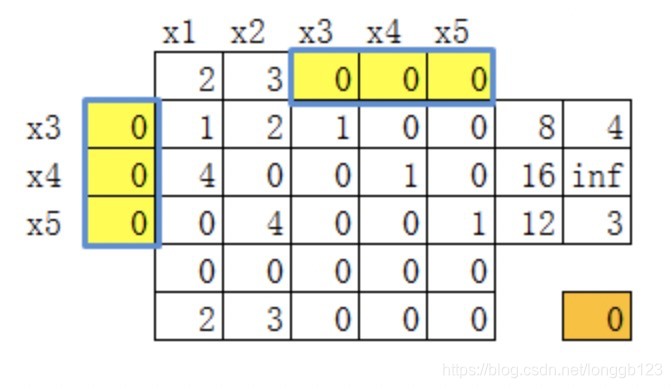
根据上面的公式，可以知道$z_0={\sum }_{i=1}^m{c}_i{b}_i$。所以很容易求出，该目标值是0。
（6）将换入换出变量迭代

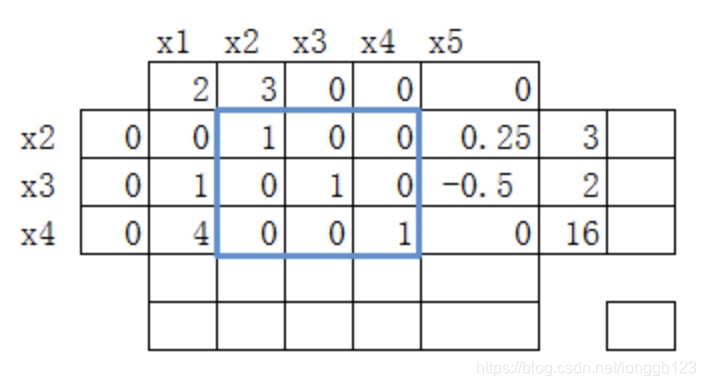
经过计算后，得出上面新的矩阵，根据单纯形法的求解方法，就可以找出最终的解。

2.4 单纯形法简版代码

通过上面的表格形式，可以把整个计算过程都梳理清楚。
下面是计算的一个简单逻辑的代码：

import numpy as np
import warnings
warnings.filterwarnings('ignore')
def simplexMethod(Object_list, Subject_list, init_bases=[], it=100):
    '''
    simplexMethod.
    '''
    def outputSimplexMethod(Object_list_len, bases, res, no_base_delta, object_v):
        '''
        Arrange the out format.
        '''
        X_vector = []
        index_str_list = no_base_delta.tolist()[0]
        base_i = 0
        no_base_i = 0
        func_str = 'z = {0} '.format(str(object_v))
        for i in range(Object_list_len):
            if base_i<len(bases) and bases[base_i]==i:
                X_vector.append(res[base_i])
                base_i += 1
            else:
                func_str += '{0} * x{1} '.format(str(index_str_list[no_base_i]), i)
                no_base_i += 1
                X_vector.append(0)
        func_str += ' \n[attention]: x{i} index i begin from 0.'
        return X_vector, func_str, object_v
    Object_list_len = len(Object_list)
    Object_m = np.matrix(Object_list)
    Subject_m = np.matrix(Subject_list)
    all_var = range(Subject_m.shape[1] - 1)
    if init_bases == []:
        len_m = int(Subject_m.shape[0])
        bases = range(len_m)
    else:
        bases = init_bases
    no_bases = list(set(all_var) - set(bases))
    object_v = None
    res = None
    no_base_delta = None
    while (it >= 0):
        it -= 1
        base_sub_m = Subject_m[:, bases]            # 取出基矩阵 m*m
        Subject_m = base_sub_m.I * Subject_m        # 计算新的subject m*n
        base_obj_m = Object_m[:, bases]            # 根据推导公式计算，z值
        z = base_obj_m * Subject_m
        delta = Object_m - z[:, :-1]                # 计算delta值，即为替换后系数
        no_base_delta = delta[:, no_bases]
        object_v = (Object_m[:, bases] * Subject_m[:, -1]).tolist()[0][0]
        res = (Subject_m[:, -1]).T.tolist()[0]
        if np.max(no_base_delta) <= 0:              # 迭代结束条件是系数都为负
            it = -1
        else:
            no_base_delta_index = np.argmax(no_base_delta)      # 正系数最大的被替入
            in_base_index = no_bases[no_base_delta_index]
            out_base_index = np.argmin(map(lambda x: x[0] if x[0] > 0 else np.inf, (Subject_m[:, -1] / Subject_m[:, in_base_index]).tolist()))      # 比例系数正最低的被替出
            bases = bases[:out_base_index] + bases[(out_base_index+1):]
            bases = bases + [in_base_index]
            bases = sorted(bases)
            no_bases = list(set(all_var) - set(bases))
    X_vector, func_str, object_v = outputSimplexMethod(Object_list_len, bases, res, no_base_delta, object_v)
    return X_vector, func_str, object_v

if __name__ == '__main__':
    Object_list = [2, 3, 0, 0, 0]
    Subject_list = [ [1, 2, 1, 0, 0,  8],
                    [4, 0, 0, 1, 0, 16],
                    [0, 4, 0, 0, 1, 12]]
    init_bases = [2, 3, 4]
    simplexMethod(Object_list, Subject_list, init_bases=init_bases, it=100)

输出结果：

([4.0, 2.0, 0, 0, 4.0],
'z = 14.0 -1.5 * x2 -0.125 * x3  \n[attention]: x{i} index i begin from 0.',
14.0)

不过，该程序版本有一个地方需要注意的是，迭代的结束条件不够严谨，即系数均为负数。
出现的问题，当系数都为负数时，但是截距却为负数，等等问题。这里就不考虑了，只是作为学习单纯形法的练习。