【20150912】NOIP模拟题解 & 总结

最新推荐文章于 2019-05-01 23:15:30 发布

longyuepeng

最新推荐文章于 2019-05-01 23:15:30 发布

阅读量485

点赞数

分类专栏：总结题解

本文链接：https://blog.csdn.net/longyuepeng/article/details/48711879

版权

总结同时被 2 个专栏收录

5 篇文章 0 订阅

订阅专栏

题解

5 篇文章 0 订阅

订阅专栏

本文是作者对一场NOIP模拟赛的题解和总结，涉及数对的分组问题、最短路径的树形DP以及平方和的线段树处理。在数对分组问题中，利用离散化和线段树实现O(nlogn)的解决方案。最短路径问题通过树形DP解决，确保罪犯被捕概率最大化。最难的平方和问题采用离线线段树，通过确定每个数的最终位置实现O(nlogM+mlogM)的算法。作者反思线段树运用不够熟练，计划加强算法巩固。

摘要由CSDN通过智能技术生成

前言

　　进击的套题系列之周末场……题目比之前做的两套简单，算是松了口气，轻松刷200分。不过还是不能大意呀，这T3改的都快吐血了……

T1_SERN的野望

　　题目大意：给出 n 对数对 (x,y) ( $1\le n\le 10^5,~1\le x,y\le10^9$ )，保证每个数对之间的 x,y 均不相同。定义数对 A 包含数对 B 当且仅当 $x_A>x_B,~y_A>y_B$ ，另定义 $F(A,S)=1$ 表示没有任何在数对集 S 中的数对 B 包含数对 A。现对这 n 对数对进行若干次分组操作，保证每个点都属于一个组。询问每个点属于的组编号。

　　分组操作如下：设当前正在进行第 cnt 次分组操作，当前仍未加入组的数对集为 S。枚举每个数对 x，如果 $F(x,S)=1$ 时将其加入第 cnt 组。

　　这题咋看有点复杂，实际上还算是比较简单的。将数对离散化后看成点。如果将所有的点按照第一维坐标从小到大排序，你会发现每次的分组操作就是“从剩余点中找出一个第一维坐标最大的点选入组中，然后找一个离当前点最近、且第二维坐标比当前点大的点，将这个点加入组后把这个点设为当前点并继续以上操作直至无法找到下一个点为止”。
　　对于找下一个点的操作，我们可以开一个线段树，其下标为每个点的第二维坐标，存入的是这个点排序后的编号。如果当前点为 $(x,y)$ ，我们只需要在线段树中查找 $[y+1,n]$ 区间的最大值，即为下一个点的编号。当然要将已加入组的点从线段树中删掉，即修改第 y 个数的值为 0。时间复杂度 $O(n\log n)$ 。

Code

#include<cstdio>
#include<iostream>
#include<algorithm>
#define fo(i,x,y) for (int i=x;i<=y;++i)
using namespace std;

const int maxn=100000+10;

struct node{
    int x,y,id;
} a[maxn];

int n,tr[maxn*4],ans[maxn];
bool f[maxn];

int max(int x,int y){ return (x>y)?x:y; }
bool cmp(node a,node b){ return (a.x<b.x || (a.x==b.x && a.y<b.y)); }

void change(int v,int l,int r,int p,int q){
    if (l==r){ tr[v]=q; return; }
    int md=(l+r)/2;
    if (p<=md) change(v*2,l,md,p,q); else change(v*2+1,md+1,r,p,q);
    tr[v]=max(tr[v*2],tr[v*2+1]);
}

int query(int v,int l,int r,int x,int y){
    if (x>y) return 0;
    if (l==x && r==y) return tr[v];
    int md=(l+r)/2;
    if (y<=md) return query(v*2,l,md,x,y);
    if (x>md) return query(v*2+1,md+1,r,x,y);
    return max(query(v*2,l,md,x,md),query(v*2+1,md+1,r,md+1,y));
}

int main(){
    freopen("sern.in","r",stdin);
    freopen("sern.out","w",stdout);
    scanf("%d",&n);
    fo(i,1,n){ scanf("%d%d",&a[i].y,&a[i].x); a[i].id=i; }
    sort(a+1,a+n+1,cmp);
    fo(i,1,n) a[i].x=a[i].y, a[i].y=i;
    sort(a+1,a+n+1,cmp);
    fo(i,1,n) change(1,1,n,a[i].y,i);
    int now=n, cnt=0;
    f[0]=1;
    while (now>0){
        ++cnt;
        int z=now;
        while (z){
            f[z]=1, ans[a[z].id]=cnt;
            change(1,1,n,a[z].y,0);
            z=query(1,1,n,a[z].y+1,n);
        }
        while (now>0 && f[now]) --now;
    }
    fo(i,1,n) printf("%d\n",ans[i]);
    return 0;
}

T2_与机关的决战

　　题目大意：有个要逃跑的罪犯初始在一个含有 n 个点、m 条无向边的图的 1 号点上 ( $1\le n\le 200,~1\le m\le 20000$ )。这个人的移动有以下规律：
　　首先，他绝对不会走一个点两次；
　　其次，每当他选择走到一个点时，他一定会走从 1 号点到这个点的最短路。保证从 1 号点走到任意点的最短路唯一。
　　每次他会从当前点能走到的所有相邻点中，随机等概率地选择一个点走。而如果他无点可走，就认为他成功逃跑了。
　　你现在要在每个点上埋伏警员抓捕他，但是他仍然有机会逃跑。一共有 S 个警员让你调配，你现在知道每个点 i 埋伏 j 名警员能成功抓捕的概率，问在最佳调配情况下，罪犯被抓住的概率。

　　由于以前已经做过类似的题，且印象深刻（这是必须的，因为一天之内做6道同一类型的题感觉那是相当的爽），看到了这题几乎是马上想到了大致的解法。
　　因为这题有个神奇的规定“只走最短路”，根据这个规则可以将原图化简为树。关于树的题目最容易想到树形DP。设 $F[i][j]$ 表示该人逃跑到以 $i$ 为根节点的子树内被抓住的概率。先考虑不在 $i$ 放任何警员，让罪犯逃跑到儿子节点 $x$ 被抓住的概率，自然有：

F [i] [j] = \sum k = 0 S F [i] [j - k] + F [ x ] [ k ] C s o n [ i ]

$F[i][j]=\sum_{k=0}^{S}F[i][j-k]+\frac{F[x][k]}{Cson[i]}$
　　其中

Cson[i] $Cson[i]$ 代表节点

i $i$ 的儿子个数。
　　然后再考虑在根节点放警员。注意罪犯可能在根节点被抓获。仿照上式就有：

F [i] [j] = \sum k = 0 S F [i] [j - k] * (1 - A [i] [k]) + A [i] [k]

$F[i][j]=\sum_{k=0}^{S}F[i][j-k]\ast(1-A[i][k])+A[i][k]$ 　　时间复杂度为均摊

O(n) $O(n)$ 。

Code

#include<cstdio>
#include<cstring>
#include<iostream>
#define fo(i,x,y) for (int i=x;i<=y;++i)
using namespace std;

const int maxn=200+10, maxm=20000+10;

int n,m,S,a[maxn],b[maxm*2][3],da[maxn],db[maxn][2],dc,cnt[maxn],dis[maxn],q[maxn*100];
double p[maxn][maxn],f[maxn][maxn];
bool pd[maxn];

void SPFA(int v){
    memset(dis,60,sizeof(dis)); dis[v]=0;
    memset(pd,1,sizeof(pd)); pd[v]=0;
    int i=0, j=1; q[1]=v;
    while (i++<j){
        for (int z=a[q[i]];z;z=b[z][2])
            if (dis[q[i]]+b[z][1]<dis[b[z][0]]){
                dis[b[z][0]]=dis[q[i]]+b[z][1];
                if (pd[b[z][0]]){
                    pd[b[z][0]]=0;
                    q[++j]=b[z][0];
                }
            }
        pd[q[i]]=1;
    }
}

void walk(int v){
    cnt[v]=0;
    for (int z=a[v];z;z=b[z][2])
        if (dis[v]+b[z][1]==dis[b[z][0]]){
            ++cnt[v];
            walk(b[z][0]);
            db[++dc][0]=b[z][0]; db[dc][1]=da[v]; da[v]=dc;
        }
}

void dp(int v){
    if (cnt[v]==0){
        fo(i,1,S) f[v][i]=p[v][i];
        return;
    }
    double gn=(double)1/cnt[v];
    for (int z=da[v];z;z=db[z][1]){
        dp(db[z][0]);
        for (int i=S;i;--i)
            fo(j,1,S){
                if (i-j<0) break;
                f[v][i]=max(f[v][i],f[v][i-j]+gn*f[db[z][0]][j]);
            }
    }
    for (int i=S;i;--i)
        fo(j,1,S){
            if (i-j<0) break;
            f[v][i]=max(f[v][i],f[v][i-j]*(1-p[v][j])+p[v][j]);
        }
}

int main(){
    freopen("battle.in","r",stdin);
    freopen("battle.out","w",stdout);
    scanf("%d%d",&n,&m);
    fo(i,1,m){
        int x,y,z;
        scanf("%d%d%d",&x,&y,&z);
        b[i*2-1][0]=y, b[i*2-1][1]=z, b[i*2-1][2]=a[x]; a[x]=i*2-1;
        b[i*2][0]=x, b[i*2][1]=z, b[i*2][2]=a[y]; a[y]=i*2;
    }
    scanf("%d",&S);
    fo(i,1,n)
        fo(j,1,S) scanf("%lf",&p[i][j]);
    SPFA(1);
    dc=0;
    walk(1);
    dp(1);
    printf("%.4lf\n",f[1][S]);
    return 0;
}

T3_平方和

　　题目大意：给出一个包含 n 个整数的序列，进行 m 次操作 ( $1\le n,m\le10^5$ )：在序列的某个数前面添加一个数；对 $[L,R]$ 内的数全部加上 X；询问 $[L,R]$ 里每个数的平方之和。

　　这道题应该是这套题中最复杂的一道题，准确的说为了改出这题我花掉了3个晚上，至少5个小时的时间……
　　这道题最重要的思想（同时也是在比赛时我差一点想到的）就是找到每个数的最终位置。如果能确定每个数的最终位置，我们就能用普通的线段树实现在线算法了。遗憾的是：显然，如果不清楚所有的插入操作，是没办法知道每个数的最终位置的。因此这题的线段树做法中，仍然只能使用离线算法——读入所有的操作，根据这些操作确定每个数的最终位置。
　　如何确定呢？显然读入所有询问之后我们可以马上知道最终序列中一共有多少个数，假设为 $M$ 。接下来设一个大小为 $M$ 的数组 $B$ ，对于 $1\le i\le M$ 初始值 $B[i]=1$ ，表示这个位置上的数仍然存在。另设一个数组 $Sum$ 表示数组 $B$ 的前缀和。如下图。
T3_01
　　我们如果倒着枚举读入的询问，那么除了插入操作外，每个询问的位置 $X$ 对应的实际位置 $Y$ 一定满足 $Sum[Y]=X$ 且 $Y$ 为所有满足上式的可能值中的最小值。
T3_02
T3_03
T3_04
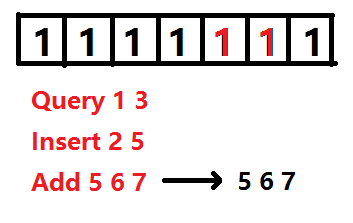
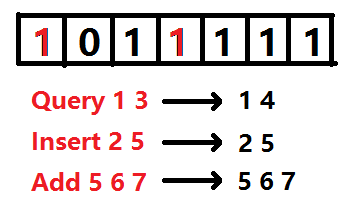
　　上述图片展示了位置变化的过程。
　　接下来考虑线段树。因为 $(x+a)^2=x^2+a^2+2ax$ ，所以对于一个区间除了要记录累加的 $a$ 的总和外，还需要记区间内 $x^2$ 的总和， $x$ 总和以及目前实际存在的 $x$ 的个数。接下来注意向下传递标记以及更新当前点标记即可。时间复杂度 $O(n\log M+m\log M)$ 。
　　PS：这题当然还有在线算法——平衡树（一般用Splay）。但是因为忙着改后面的题目，暂时放下了平衡树的学习。学完了就发学习心得上来。

Code

#include<cstdio>
#include<iostream>
#define fo(i,x,y) for (int i=x;i<=y;++i)
using namespace std;

const int maxm=100000+10, maxn=maxm+100000+10, mod=7459;

struct node{
    int x,y,sa,cnt;
} a[maxn*3];

int n,m,b[maxn],q[maxm][4];
char str[10];

void mark(int v,int l,int r){
    a[v].cnt=r-l+1; a[v].x=a[v].y=a[v].sa=0;
    if (l==r) return;
    int md=(l+r)/2; mark(v*2,l,md); mark(v*2+1,md+1,r);
}

int place(int v,int l,int r,int x,int del){
    if (l==r){ a[v].cnt-=del; return l; }
    int ret,md=(l+r)/2;
    if (x<=a[v*2].cnt) ret=place(v*2,l,md,x,del);
    else ret=place(v*2+1,md+1,r,x-a[v*2].cnt,del);
    a[v].cnt-=del;
    return ret;
}

int calc(int v){
    return ((2*a[v].y*a[v].sa+a[v].sa*a[v].sa%mod*a[v].cnt)%mod+mod)%mod;
}

void down(int v){
    int l=v*2, r=v*2+1;
    if (a[l].cnt) a[l].sa=(a[l].sa+a[v].sa)%mod;
    if (a[r].cnt) a[r].sa=(a[r].sa+a[v].sa)%mod;
    a[v].sa=0;
}

void update(int v){
    int l=v*2, r=v*2+1;
    a[v].x=(a[l].x+a[r].x+calc(l)+calc(r))%mod;
    a[v].y=(a[l].y+a[r].y+a[l].sa*a[l].cnt+a[r].sa*a[r].cnt)%mod;
    a[v].cnt=a[l].cnt+a[r].cnt;
}

void maketree(int v,int l,int r,int st){
    a[v].sa=0;
    if (l==r){
        if (!a[v].cnt) return;
        a[v].x=b[st]*b[st]%mod;
        a[v].y=b[st]%mod;
        return;
    }
    int md=(l+r)/2;
    maketree(v*2,l,md,st);
    maketree(v*2+1,md+1,r,st+a[v*2].cnt);
    update(v);
}

void ins(int v,int l,int r,int p,int q){
    if (l==r){
        a[v].x=q*q%mod;
        a[v].y=q%mod;
        a[v].sa=0;
        ++a[v].cnt;
        return;
    }
    down(v);
    int md=(l+r)/2;
    if (p<=md) ins(v*2,l,md,p,q); else ins(v*2+1,md+1,r,p,q);
    update(v);
}

void add(int v,int l,int r,int x,int y,int z){
    if (l==x && r==y){
        if (a[v].cnt) a[v].sa=(a[v].sa+z)%mod;
        return;
    }
    down(v);
    int md=(l+r)/2;
    if (y<=md) add(v*2,l,md,x,y,z);
    else if (x>md) add(v*2+1,md+1,r,x,y,z);
    else {
        add(v*2,l,md,x,md,z);
        add(v*2+1,md+1,r,md+1,y,z);
    }
    update(v);
}

int query(int v,int l,int r,int x,int y){
    if (l==x && r==y) return (a[v].x+calc(v))%mod;
    down(v);
    int md=(l+r)/2, ret;
    if (y<=md) ret=query(v*2,l,md,x,y);
    else if (x>md) ret=query(v*2+1,md+1,r,x,y);
    else ret=(query(v*2,l,md,x,md)+query(v*2+1,md+1,r,md+1,y))%mod;
    update(v);
    return ret;
}

int main(){
    freopen("sqrsum.in","r",stdin);
    freopen("sqrsum.out","w",stdout);
    scanf("%d",&n);
    fo(i,1,n) scanf("%d",&b[i]);
    scanf("%d",&m);
    fo(i,1,m){
        scanf("%s%d%d",str,&q[i][1],&q[i][2]);
        if (str[0]=='I') q[i][0]=0, ++n;
        if (str[0]=='A'){ q[i][0]=1; scanf("%d",&q[i][3]); }
        if (str[0]=='Q') q[i][0]=2;
    }
    mark(1,1,n);
    for (int i=m;i;--i)
        if (q[i][0]) q[i][1]=place(1,1,n,q[i][1],0), q[i][2]=place(1,1,n,q[i][2],0);
        else q[i][1]=place(1,1,n,q[i][1],1);
    maketree(1,1,n,1);
    fo(i,1,m)
        if (q[i][0]==0) ins(1,1,n,q[i][1],q[i][2]);
        else if (q[i][0]==1) add(1,1,n,q[i][1],q[i][2],q[i][3]);
        else printf("%d\n",query(1,1,n,q[i][1],q[i][2]));
    return 0;
}

总结

　　这套题难度真的不怎么大（相比之前的两套题），但是T3的线段树实在是太难改了-_-。改完总结原因，还是因为对线段树的不熟练——基本原则“每次需要分割一个区间操作时需要下传标记”总是忘记，也因此程序出现了各种各样的奇妙错误。以我现在的水平，只靠阅读程序并不能直接发现问题，只能老实单步调试，时间都花在这上面。看来改完题之后，也该开始巩固一些学了很久的算法了！